Matalab之模糊KMeans实现

这节继续上节的KMeans进行介绍，上节主要是对模糊KMeans方法的原理做了介绍，没有实践印象总是不深刻，前段时间有个师姐让我帮着写了个模糊KMeans的算法，今天就拿她给出的例子来对这个方法做个实践讲解。她给的数据是n个行业在m年内的资源消耗参数，想通过FCM算法对这些行业进行聚类，从而在能耗上对它们进行分类。处理的数据很简单，所以用FCM这种简单的聚类算法就足可以达到要求了。给出数据的一角：

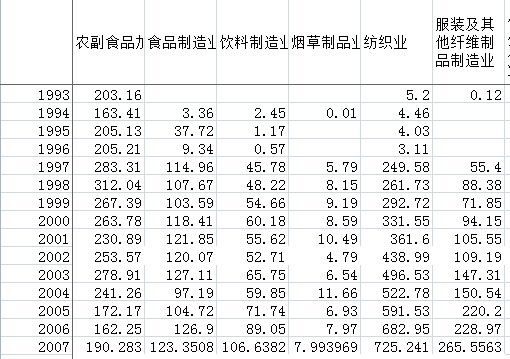
具体处理过程我就不啰嗦了，核心思想就是FCM算法，给出一个具体的流程图

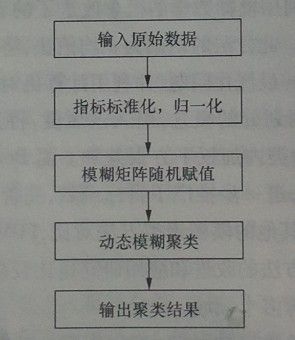
根据步骤我将算法实现分成了五个子函数和一个主函数，直接上代码（其中有详细的解释）

% 子函数1

function U = initfcm(cluster_n, data_n)

% 初始化fcm的隶属度函数矩阵

% 输入:

%   cluster_n   ---- 聚类中心个数

%   data_n      ---- 样本点数

% 输出：

%   U           ---- 初始化的隶属度矩阵

U = rand(cluster_n, data_n);

col_sum = sum(U);

U = U./col_sum(ones(cluster_n, 1), :);

% 子函数2

function [U_new, center, obj_fcn] = stepfcm(data, U, cluster_n, expo)

% 模糊C均值聚类时迭代的一步

% 输入：

%   data        ---- nxm矩阵,表示n个样本,每个样本具有m的维特征值

%   U           ---- 隶属度矩阵

%   cluster_n   ---- 标量,表示聚合中心数目,即类别数

%   expo        ---- 隶属度矩阵U的指数                      

% 输出：

%   U_new       ---- 迭代计算出的新的隶属度矩阵

%   center      ---- 迭代计算出的新的聚类中心

%   obj_fcn     ---- 目标函数值

mf = U.^expo;       % 隶属度矩阵进行指数运算结果

center = mf*data./((ones(size(data, 2), 1)*sum(mf'))'); % 新聚类中心(5.4)式

dist = distfcm(center, data);       % 计算距离矩阵

obj_fcn = sum(sum((dist.^2).*mf));  % 计算目标函数值 (5.1)式

tmp = dist.^(-2/(expo-1));     

U_new = tmp./(ones(cluster_n, 1)*sum(tmp));  % 计算新的隶属度矩阵 (5.3)式

% 子函数3

function out = distfcm(center, data)

% 计算样本点距离聚类中心的距离

% 输入：

%   center     ---- 聚类中心

%   data       ---- 样本点

% 输出：

%   out        ---- 距离

out = zeros(size(center, 1), size(data, 1));

for k = 1:size(center, 1), % 对每一个聚类中心

    % 每一次循环求得所有样本点到一个聚类中心的距离

    out(k, :) = sqrt(sum(((data-ones(size(data,1),1)*center(k,:)).^2)',1));

end

% 子函数4

function DataOut = Unitfcm(DataOrg)

% 对输入数据进行标准化和归一化处理

% 输入：

%   DataOrg       ---- 样本数据

% 输出：

%   DataOut        ---- 归一化数据

X_col=sum(DataOrg,1)./size(DataOrg,1);

S_col=sqrt(sum((DataOrg-X_col(ones(size(DataOrg,1),1),:)).^2,1)./(size(DataOrg,1)-1));

DataUnit=(DataOrg-X_col(ones(size(DataOrg,1),1),:))./S_col(ones(size(DataOrg,1),1),:);%标准化结果

C_col=max(abs(DataUnit),[],1);

DataOut=(DataUnit+C_col(ones(size(DataUnit,1),1),:))./(2*C_col(ones(size(DataUnit,1),1),:));%归一化后的结果

% 子函数5

function ShowResult(U)

% 呈现聚类结果

% 输入：

%   U       ---- 隶属度矩阵

for i=1:size(U,2)

    data=U(:,i);

    [row,col]=find(data==max(data));

    disp(['第',num2str(i),'个样本属于',num2str(row),'类']);

end

function [center, U, obj_fcn] = FCMClust(data, cluster_n, options)

% FCMClust.m   采用模糊C均值对数据集data聚为cluster_n类 

% 用法：

%   1.  [center,U,obj_fcn] = FCMClust(Data,N_cluster,options);

%   2.  [center,U,obj_fcn] = FCMClust(Data,N_cluster);

% 输入：

%   data        ---- nxm矩阵,表示n个样本,每个样本具有m的维特征值

%   N_cluster   ---- 标量,表示聚合中心数目,即类别数

%   options     ---- 4x1矩阵，其中

%       options(1):  隶属度矩阵U的指数，>1                  (缺省值: 2.0)

%       options(2):  最大迭代次数                           (缺省值: 100)

%       options(3):  隶属度最小变化量,迭代终止条件           (缺省值: 1e-5)

%       options(4):  每次迭代是否输出信息标志                (缺省值: 1)

% 输出：

%   center      ---- 聚类中心

%   U           ---- 隶属度矩阵

%   obj_fcn     ---- 目标函数值

%   Example:

%       data = rand(100,2);

%       [center,U,obj_fcn] = FCMClust(data,2);

%       plot(data(:,1), data(:,2),'o');

%       hold on;

%       maxU = max(U);

%       index1 = find(U(1,:) == maxU);

%       index2 = find(U(2,:) == maxU);

%       line(data(index1,1),data(index1,2),'marker','*','color','g');

%       line(data(index2,1),data(index2,2),'marker','*','color','r');

%       plot([center([1 2],1)],[center([1 2],2)],'*','color','k')

%       hold off;

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%



if nargin ~= 2 & nargin ~= 3,    %判断输入参数个数只能是2个或3个

    error('Too many or too few input arguments!');

end



data_n = size(data, 1); % 求出data的第一维(rows)数,即样本个数

in_n = size(data, 2);   % 求出data的第二维(columns)数，即特征值长度

% 默认操作参数

default_options = [2;    % 隶属度矩阵U的指数

    100;                % 最大迭代次数 

    1e-5;               % 隶属度最小变化量,迭代终止条件

    1];                 % 每次迭代是否输出信息标志 



if nargin == 2,

    options = default_options;

 else       %分析有options做参数时候的情况

    % 如果输入参数个数是二那么就调用默认的option;

    if length(options) < 4, %如果用户给的opition数少于4个那么其他用默认值;

        tmp = default_options;

        tmp(1:length(options)) = options;

        options = tmp;

    end

    % 返回options中是数的值为0(如NaN),不是数时为1

    nan_index = find(isnan(options)==1);

    %将denfault_options中对应位置的参数赋值给options中不是数的位置.

    options(nan_index) = default_options(nan_index);

    if options(1) <= 1, %如果模糊矩阵的指数小于等于1

        error('The exponent should be greater than 1!');

    end

end

%将options 中的分量分别赋值给四个变量;

expo = options(1);          % 隶属度矩阵U的指数

max_iter = options(2);        % 最大迭代次数 

min_impro = options(3);        % 隶属度最小变化量,迭代终止条件

display = options(4);        % 每次迭代是否输出信息标志 



obj_fcn = zeros(max_iter, 1);    % 初始化输出参数obj_fcn



U = initfcm(cluster_n, data_n);     % 初始化模糊分配矩阵,使U满足列上相加为1,



%添加输入数据归一化处理

DataInfo=Unitfcm(data);



% Main loop  主要循环

for i = 1:max_iter,

    %在第k步循环中改变聚类中心ceneter,和分配函数U的隶属度值;

    [U, center, obj_fcn(i)] = stepfcm(DataInfo, U, cluster_n, expo);

    if display, 

        fprintf('FCM:Iteration count = %d, obj. fcn = %f\n', i, obj_fcn(i));

    end

    % 终止条件判别

    if i > 1,

        if abs(obj_fcn(i) - obj_fcn(i-1)) < min_impro, 

            

            break;

        end,

    end

end



iter_n = i;    % 实际迭代次数 

obj_fcn(iter_n+1:max_iter) = [];

OK，结束了，但愿能对减少大家的工作量带来帮助。