A Bug's Life(hdu1829种类并查集)
题意：有一群虫子，现在给你一些关系，判断这些关心有没有错
思路：向量种类并查集，下面讲一下向量的种类并查集
本题的各个集合的关心有两种0同性，1异性，怎么判断有错，
1.先判断他们是否在一个集合，即父亲是否相同，若父亲相同，用向量算的父亲之间的关系和之前的关心有矛盾没，有矛盾就是有错。
2.如果不在一个集合，就合并他们的父亲，用向量根据根节点的关心求出父亲的关心，然后合并。
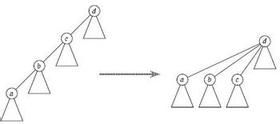
这是并查集的重要的操作路径压缩，路径压缩的时候关心就要更新比如 1- 2 是异性 2 - 3 是异性 那么1,2,3在同一集合父亲都是1，压缩过后1和3就是同性
这就路径压缩时的关系更新，关键是怎么更新呢？
假设 x 的父亲节点rootx,rootx的父亲是rootxx
RC4@A@JMZ{JJ.jpg)
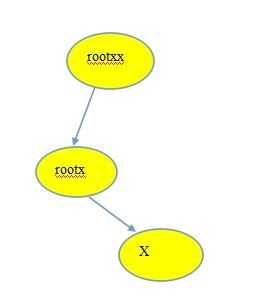
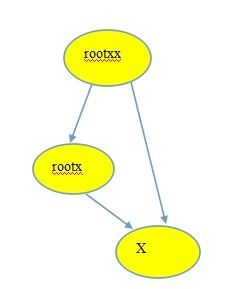
图一 是合并前图二 是合并时
有点像向量，向量加法首尾相接 所以rootxx和x的关系就是 (rootxx --> rootx + rootx-->x) % 2;
同理根据孩子节点推理父亲关系的时候也是
假设x的父亲rootx y的父亲rooty 合并时x的父亲是y，如图
如果想要知道rootx --> rooty的关系，rootx--> x + x --> y + y --> rooty
因为向量是相反为负的所以 y-->rooty = 2 - rooty-->y;
所以 rootx --> rooty = rootx--> x + x --> y + 2 - rooty-->y;
以为 题目x -- > y 为1 所以 rootx --> rooty = rootx--> x +1 + 2 - rooty-->y;
向量一定要注意方向，一定是父亲指向儿子，不能弄反。
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
struct bian
{
int parent;
int relation;
}p[10005];
void Make_set(int n)
{
int i;
for(i = 0; i < n; i++)
{
p[i].parent = i;
p[i].relation = 0;
}
}
int Find_set(int x)
{
if(x != p[x].parent)
{
int temp = p[x].parent;
p[x].parent = Find_set(p[x].parent);
p[x].relation = (p[temp].relation+p[x].relation) % 2;
}
return p[x].parent;
}
int main()
{
int t,cas = 0;
scanf("%d",&t);
while(t--)
{
int n,m;
scanf("%d%d",&n,&m);
int i,a,b,sum = 0;
Make_set(n);
for(i = 0; i < m; i++)
{
scanf("%d%d",&a,&b);
int x = Find_set(a);
int y = Find_set(b);
if(x == y)
{
if(1 != ( 2 - p[a].relation + p[b].relation ) % 2)
{
sum++;
}
}
else
{
p[x].parent = y;
p[x].relation = (p[a].relation + 3 - p[b].relation) % 2;
}
}
printf("Scenario #%d:\n",++cas);
if(sum)
{
printf("Suspicious bugs found!\n\n");
}
else
{
printf("No suspicious bugs found!\n\n");
}
}
return 0;
}