leetcode—word ladder II

1.题目描述

Given two words (start and end), and a dictionary, find all shortest transformation sequence(s) from start to end, such that:   Only one letter can be changed at a time Each intermediate word must exist in the dictionary For example,   Given: start = "hit" end = "cog" dict = ["hot","dot","dog","lot","log"]   Return   [ ["hit","hot","dot","dog","cog"], ["hit","hot","lot","log","cog"] ]

2.解题思路

我一看到这个题目就觉得类似于最小生成树，应该用贪心算法来做，贪心算法的思路如下：

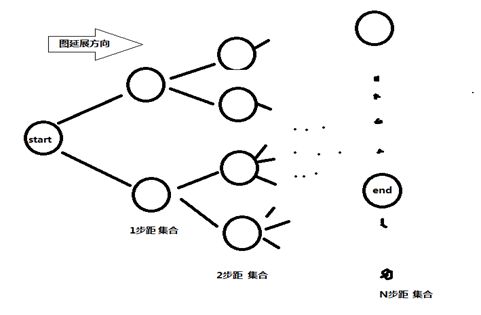
       从start串出发，找出一次变换可以得到的string串的集合S₁，如果集合S₁中包含有end串，那么搜索结束，否则，搜索两步之内能到达的串的集合S₂，同样判断两步之内能到达的串集合中是否有end串，以此类推，最终找到最短路径。另外，路径保存需要单独设置一个数据结构，

最终算法描述如下（类最小生成树）：

1. 将字典dict中的所有字符串分为左右两侧，一侧为leftside=start(实际编码不需存储)，一侧为rightside=(dict-start),当前距start最远的节点，比如说从start i 步之内可达的节点集合curStep = start （因为初始是0步可达）。
2. 计算nextStep，也就是 i+1 步可达的字符串集合，最简单的思路就是下面的思路，遍历curStep 遍历rightside，逐个比较，必然能找到nextStep，找到nextStep之后curStep 变成了nextStep,将nextStep 中的字符串从rightside里面抹去，nextStep清空继续寻找直至找到的nextStep或rightside为空（表示没有路径到end），或者end被发现。

于是有了下面的这份代码：

class Solution { public: vector<vector<string> > findLadders(string start, string end, unordered_set<string> &dict) { // end typing your C/C++ solution below // DO NOT write int main() function //[email protected]   map<string,vector<string> > path;   unordered_set<string>leftside; unordered_set<string>rightside=dict; rightside.insert(start); rightside.insert(end);   leftside.insert(start); rightside.erase(start);   unordered_set<string>curStep; unordered_set<string>nextStep; curStep.insert(start); while(curStep.find(end)==curStep.end()&&!rightside.empty()) { unordered_set<string>::iterator iter_us_cur; unordered_set<string>::iterator iter_us_right;   for(iter_us_cur=curStep.begin();iter_us_cur!=curStep.end();++iter_us_cur) {   for(iter_us_right=rightside.begin();iter_us_right!=rightside.end();++iter_us_right) { if(isCvtable(*iter_us_cur,*iter_us_right)) { if(path.find(*iter_us_cur)!=path.end()) { path[*iter_us_cur].push_back(*iter_us_right); } else { vector<string> emptyV; path[*iter_us_cur]=emptyV; path[*iter_us_cur].push_back(*iter_us_right); }   nextStep.insert(*iter_us_right); } }   }   if(nextStep.empty())break; for(iter_us_right=nextStep.begin();iter_us_right!=nextStep.end();++iter_us_right) { rightside.erase(*iter_us_right); } curStep = nextStep; nextStep.clear(); }   vector<vector<string> > result; vector<string> temp;   if(curStep.find(end)!=curStep.end()) { output(path,start,end,result,temp); }   return result;   } bool isCvtable(string str1,string str2) { //cout<<"isCvtable: "<<str1<<str2<<endl; if(str1.length()!=str2.length()){return false;} int count=0; for(int i = 0;i<str1.length();++i) { if(str1[i]!=str2[i])count++; if(count>1)return false; } return count==1; }     void output(map<string,vector<string> >&path,string start,string end,vector<vector<string> >&result,vector<string> & temp) { temp.push_back(start);   if(start==end) { result.push_back(temp);return; }   vector<string>::iterator iter_v; for(iter_v=path[start].begin();iter_v!=path[start].end();++iter_v) { output(path,*iter_v,end,result,temp);temp.pop_back(); } } };

 

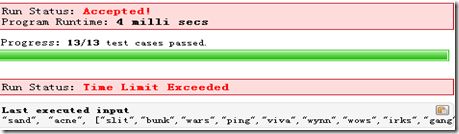
提交online judge之后，小数据集没问题，大数据集却TLE了，分析了一下，主要是从curStep求nextStep的过程太耗时，我这个是O(N²)的时间复杂度，结果如下：

挂掉的这个案例大概有3000个词，很大，分析了一下，题目给的参数是unordered_set是有用意的，unordered_set实际底层是个hash表，所以能够常数时间索引一个字符串，基于这个思路，在已知curStep、rightside求nextStep的过程中：

        对每一个curStep中的字符串，假设长度为M，那么它的每位有25种变化，也就是每个单词有25*M中变化，那么时间复杂度就变成了O(MN)，单词长度一般不会太大，所以这个是个线性的算法，分析完毕，我开始着手写算法：

class Solution { public: vector<vector<string> > findLadders(string start, string end, unordered_set<string> &dict) { // end typing your C/C++ solution below // DO NOT write int main() function //[email protected]   map<string,vector<string> > path;   unordered_set<string>rightside=dict;   rightside.erase(start); unordered_set<string>curStep; unordered_set<string>nextStep; curStep.insert(start); while(curStep.find(end)==curStep.end()&&!rightside.empty()) { unordered_set<string>::iterator iter_us_cur; for(iter_us_cur=curStep.begin();iter_us_cur!=curStep.end();++iter_us_cur) { string temp; for(int i=0;i<(*iter_us_cur).length();++i) { for(int j = 0;j<26;j++) { temp = *iter_us_cur; if(temp[i]!=('a'+j)) { temp[i] = ('a'+j); } if(rightside.count(temp)==1) { nextStep.insert(temp); if(path.find(*iter_us_cur)==path.end()) { vector<string> emptyV; path.insert(make_pair(*iter_us_cur,emptyV)); } path[*iter_us_cur].push_back(temp); } } } } if(nextStep.empty())break; unordered_set<string>::iterator iter_set; for(iter_set=nextStep.begin();iter_set!=nextStep.end();++iter_set) { rightside.erase(*iter_set); } curStep = nextStep; nextStep.clear(); } vector<vector<string> > result; vector<string> temp; if(curStep.find(end)!=curStep.end()) { output(path,start,end,result,temp); }   return result;   } void output(map<string,vector<string> >&path,string start,string end,vector<vector<string> >&result,vector<string> & temp) { temp.push_back(start);   if(start==end) { result.push_back(temp);return; }   vector<string>::iterator iter_v; for(iter_v=path[start].begin();iter_v!=path[start].end();++iter_v) { output(path,*iter_v,end,result,temp);temp.pop_back(); } } };

 

结果出来的一瞬间很美妙：

另外，输出结果的方式也有改进的余地，如图所示，程序中的path实际是这么一张图，实际就是一张邻接表。

我的算法是从start开始深度搜索，直至找到end，当搜索到的最后一个节点不是end的时候其实都是无效搜索（而且比重很大），所以可以把上述这幅图反过来，然后从end开始反向搜索，以空间换时间。