POJ 3124 The Bookcase【dp]

Description

No wonder the old bookcase caved under the massive piles of books Tom had stacked 
on it. He had better build a new one, this time large enough to hold all of his books. Tomfinds it practical to have the books close at hand when he works at his desk. Therefore, he is imagining a compact solution with the bookcase standing on the back of the desk. Obviously, this would put some restrictions on the size of the bookcase, it should preferably be as small as possible. In addition, Tom would like the bookcase to have exactly three shelves for aesthetical reasons. 

Wondering how small his bookcase could be, he models the problem as follows. He measures the height hi and thickness ti of each book i and he seeks a partition of the books in three non-empty sets S1, S2, S3 such that 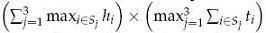 is minimized, i.e. the area of the bookcase as seen when standing in front of it (the depth needed is obviously the largest width of all his books, regardless of the partition). Note that this formula does not give the exact area of the bookcase, since the actual shelves cause a small additional height, and the sides cause a small additional width. For simplicity, we will ignore this small discrepancy. 

Thinking a moment on the problem, Tom realizes he will need a computer program to do the job.

Input

The input begins with a positive number on a line of its own telling the number of test cases (at most 20). For each test case there is one line containing a single positive integer N, 3 ≤ N ≤ 70 giving the number of books. Then N lines follow each containing two positive integers hi, ti, satisfying 150 ≤ hi ≤ 300 and 5 ≤ ti ≤ 30, the height and thickness of book i respectively, in millimeters.

Output

For each test case, output one line containing the minimum area (height times width) of a three-shelf bookcase capable of holding all the books, expressed in square millimeters.

Sample Input

2

4

220 29

195 20

200 9

180 30

6

256 20

255 30

254 15

253 20

252 15

251 9

Sample Output

18000

29796

题意：求出将n本书全部放在三层书架上，求出最大宽度和高度和的最小值
思路： dp[i][j][k]表示前i本书第二层高度为j, 第三层高度为k的总高度的最小值
状态转移方程为：
　　dp[i][j][k]= {   dp[i-1][j][k]; //第i本书放在第一层；
　　　　　　　　　　dp[i-1][j][k]+book[i].h; //j==0第二层还没有书本
　　　　　　　　　　dp[i-1][j+boo[i].w][k]; //第i本书放在第二层且非第二层的第一本书
　　　　　　　　　　dp[i-1][j][k]+book[i].h; //k==0第三层还没有书本
　　　　　　　　　　dp[i-1][j][k+book[i].w]; //第i本书放在第三层且非第三层的第一本书
　　　　　　　　}
　　那么就可以考虑给空间优化，dp设成二维数组 dp[i][j]表示后两层宽度为i, j中高度的最小值；
　　第二层放的书取决于前一层的宽度；第三层放的书取决于前两层；
　　将高度按照由大到小排序， 宽度有小到大；
　　但是高度和要求整体最优最后枚举所有的宽度的总和，求出总面积的最小；
　　dp[j][k]={

　　　　　　　　 j==0, a=book[i].h; dp[j+book[i].w][k]=min(dp[j+book[i].w][k], d[[j][k]+a);
　　　　　　　　k==0, a=book[i].h; d[j][k+book[i].w]=min(d[j][k+book[i].w], d[[j][k]+a)
　　　　　　　}

代码如下：

View Code

#include<stdio.h>

#include<string.h>

#include<iostream>

#include<algorithm> 

using namespace std;

#define N 71

#define M 31 

#define Max 999999

int dp[N*M][N*M];  

struct Book

{

    int h, w;

}; 

int cmp(Book x, Book y)

{

    if(x.h!=y.h)

        return x.h>y.h;

    return x.w<y.w;

} 

int main()

{

    int T, i, j, n, sum, k;

    scanf("%d", &T);

    while(T--)

    {

        Book book[N]; 

        scanf("%d", &n);

        sum=0; 

        for(i=1; i<=n; i++)

        {

            scanf("%d%d", &book[i].h, &book[i].w);

            sum+=book[i].w;

        }

        sort(book+1, book+n+1, cmp);

        for(i=0; i<=sum; i++)

            for(j=0; j<=sum; j++)

                dp[i][j]=Max;

        dp[0][0]=0;

        int noww=0; 

        for(i=2; i<=n; i++)

        {

            for(j=noww; j>=0; j--)

            {

                for(k=noww; k>=0; k--)

                {

                    if(dp[j][k]==Max)    

                        continue; 

                    if(noww-j-k<0)

                         continue;

                    int a=0; 

                    if(j==0)

                        a=book[i].h;

                    dp[j+book[i].w][k]=min(dp[j+book[i].w][k], dp[j][k]+a);

                    a=0; 

                    if(k==0)

                        a=book[i].h;

                    dp[j][k+book[i].w]=min(dp[j][k+book[i].w], dp[j][k]+a);

                } 

            }

            noww+=book[i].w;

        }

        int minnum=Max;

        for(j=1; j<=noww; j++)

        {

            for(k=1; k<=noww; k++)

            {

                if(dp[j][k]==Max)

                    continue;

                if(sum-j-k<=0)

                    continue;

                int maxw=max(j, k);

                maxw=max(maxw, sum-j-k); 

                minnum=min(minnum, maxw*(dp[j][k]+book[1].h));

            }

        } 

        printf("%d\n", minnum);

    }

}