图的存储结构(十字链表、邻接多重表、边集数组)- 数据结构和算法58
图的存储结构(十字链表、邻接多重表、边集数组)
让编程改变世界
Change the world by program
十字链表
邻接表固然优秀,但也有不足,例如对有向图的处理上,有时候需要再建立一个逆邻接表~ 那我们思考了:有没有可能把邻接表和逆邻接表结合起来呢? 答案是肯定的,这就是我们现在要谈的十字链表(Orthogonal List) 为此我们重新定义顶点表结点结构: [caption id="attachment_2536" align="alignnone" width="470"]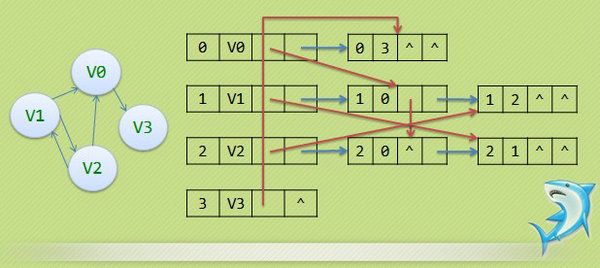 十字链表[/caption] 十字链表的好处就是因为把邻接表和逆邻接表整合在了一起,这样既容易找到以Vi为尾的弧,也容易找到以Vi为头的弧,因而容易求得顶点的出度和入度。 十字链表除了结构复杂一点外,其实创建图算法的时间复杂度是和邻接表相同的,因此,在有向图的应用中,十字链表也是非常好的数据结构模型。
十字链表[/caption] 十字链表的好处就是因为把邻接表和逆邻接表整合在了一起,这样既容易找到以Vi为尾的弧,也容易找到以Vi为头的弧,因而容易求得顶点的出度和入度。 十字链表除了结构复杂一点外,其实创建图算法的时间复杂度是和邻接表相同的,因此,在有向图的应用中,十字链表也是非常好的数据结构模型。
邻接多重表
讲了有向图的优化存储结构,对于无向图的邻接表,有没有问题呢? 如果我们在无向图的应用中,关注的重点是顶点的话,那么邻接表是不错的选择,但如果我们更关注的是边的操作,比如对已经访问过的边做标记,或者删除某一条边等操作,邻接表就显得不那么方便了。 到底有多烦?小甲鱼用图片告诉你: 若要删除(V0,V2)这条边,就需要对邻接表结构中边表的两个结点进行删除操作。 [caption id="attachment_2539" align="alignnone" width="515"]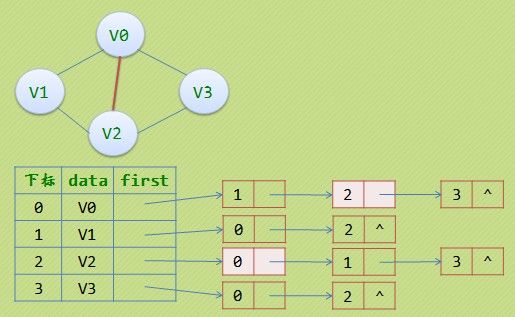 邻接多重表[/caption] 因此,我们也仿照十字链表的方式,对边表结构进行改装,重新定义的边表结构如下:
邻接多重表[/caption] 因此,我们也仿照十字链表的方式,对边表结构进行改装,重新定义的边表结构如下:
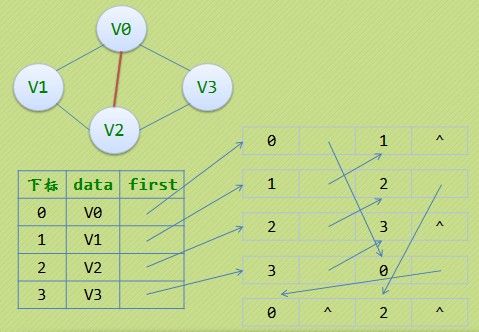 邻接多重表[/caption]
邻接多重表[/caption]
边集数组
边集数组是由两个一维数组构成,一个是存储顶点的信息,另一个是存储边的信息,这个边数组每个数据元素由一条边的起点下标(begin)、终点下标(end)和权(weight)组成。 [caption id="attachment_2542" align="alignnone" width="528"]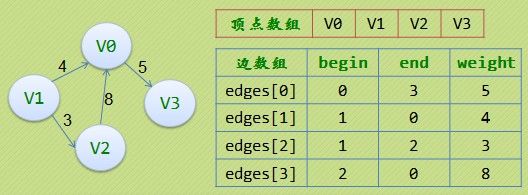 边集数组[/caption]
边集数组[/caption]
弗洛伊德的冰山理论
[caption id="attachment_2543" align="alignnone" width="333"]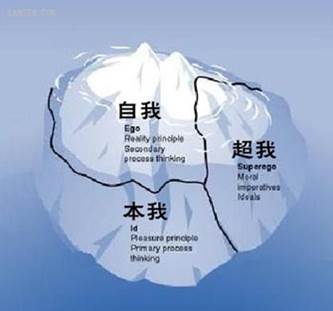 冰山理论[/caption] [buy]
获得所有教学视频、课件、源代码等资源打包 [/buy] [Downlink href='http://kuai.xunlei.com/d/BdsUAwKDswCd9YtR18a']视频下载[/Downlink]
冰山理论[/caption] [buy]
获得所有教学视频、课件、源代码等资源打包 [/buy] [Downlink href='http://kuai.xunlei.com/d/BdsUAwKDswCd9YtR18a']视频下载[/Downlink]