机器学习理论与实战（十）K均值聚类和二分K均值聚类

        接下来就要说下无监督机器学习方法，所谓无监督机器学习前面也说过，就是没有标签的情况，对样本数据进行聚类分析、关联性分析等。主要包括K均值聚类（K-means clustering）和关联分析，这两大类都可以说的很简单也可以说的很复杂，学术的东西本身就一直在更新着。比如K均值聚类可以扩展一下形成层次聚类（Hierarchical Clustering），也可以进入概率分布的空间进行聚类，就像前段时间很火的LDA聚类,虽然最近深度玻尔兹曼机（DBM）打败了它，但它也是自然语言处理领域(NLP:Natural Language Processing)的一个有力工具，有过辉煌的一段故事。而关联性分析又是另外一个比较有力的工具，它又称购物篮分析，我们可以大概可以体会到它的用途，挖掘目标之间的关联性，经典的故事就是啤酒和尿布的关联。另外多说一下，google最近的两大核心技术：深度学习和知识图，深度学习就不说了，而知识图就是挖掘关系的。找到了关系就找到了金矿，关系也可以用复杂网络（complex network）来建模。这些话题就打住吧，今天就来说下K均值聚类和二分K均值聚类。

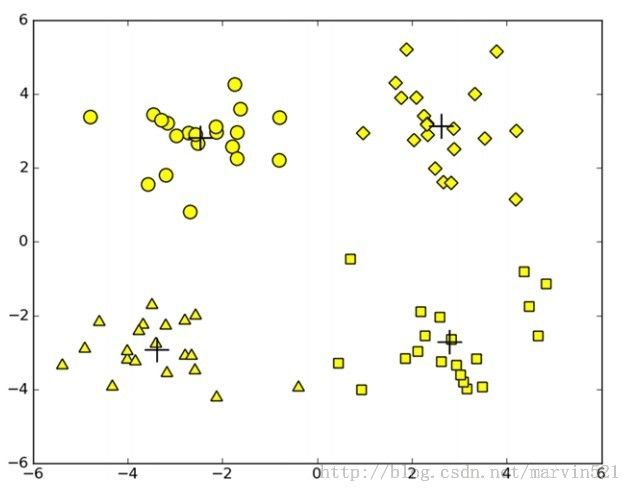
       K均值聚类比较简单，再说原理之前，先来看个样本图，如（图一）所示：

 

（图一）

       假如（图一）中是我们的样本数据，每个样本都没有类别，我们想对他们简单的划下类，在（图一）中明显的有四“堆”数据，我们用什么方法能把他们分成四类呢？K均值聚类就是解决这种问题的(好腻 = =!)，K均值聚类的原理如下：

随机的分配K个质心（上图中K为4）

如果样本中任意一个数据点归属的簇号（堆类别）发生改变

遍历每一个样本点

    遍历每一个质心

           计算数据点到质心的距离

    把数据点分配到距其最近的簇

    对每一个簇，重新计算簇中所有样本点的均值作为质心

 

K均值简单的一句话总结就是：更新质心，更新每个样本的所属的类别。按照上述更新规则，当没有样本的簇号发生改变了，迭代也就终止咯。下面就来看看代码吧：

 

from numpy import *



def loadDataSet(fileName):      #general function to parse tab -delimited floats

    dataMat = []                #assume last column is target value

    fr = open(fileName)

    for line in fr.readlines():

        curLine = line.strip().split('\t')

        fltLine = map(float,curLine) #map all elements to float()

        dataMat.append(fltLine)

    return dataMat



def distEclud(vecA, vecB):

    return sqrt(sum(power(vecA - vecB, 2))) #la.norm(vecA-vecB)



def randCent(dataSet, k):

    n = shape(dataSet)[1]

    centroids = mat(zeros((k,n)))#create centroid mat

    for j in range(n):#create random cluster centers, within bounds of each dimension

        minJ = min(dataSet[:,j]) 

        rangeJ = float(max(dataSet[:,j]) - minJ)

        centroids[:,j] = mat(minJ + rangeJ * random.rand(k,1))

    return centroids

    

def kMeans(dataSet, k, distMeas=distEclud, createCent=randCent):

    m = shape(dataSet)[0]

    clusterAssment = mat(zeros((m,2)))#create mat to assign data points 

                                      #to a centroid, also holds SE of each point

    centroids = createCent(dataSet, k)

    clusterChanged = True

    while clusterChanged:

        clusterChanged = False

        for i in range(m):#for each data point assign it to the closest centroid

            minDist = inf; minIndex = -1

            for j in range(k):

                distJI = distMeas(centroids[j,:],dataSet[i,:])

                if distJI < minDist:

                    minDist = distJI; minIndex = j

            if clusterAssment[i,0] != minIndex: clusterChanged = True

            clusterAssment[i,:] = minIndex,minDist**2

        print centroids

        for cent in range(k):#recalculate centroids

            ptsInClust = dataSet[nonzero(clusterAssment[:,0].A==cent)[0]]#get all the point in this cluster

            centroids[cent,:] = mean(ptsInClust, axis=0) #assign centroid to mean 

    return centroids, clusterAssment

 

 

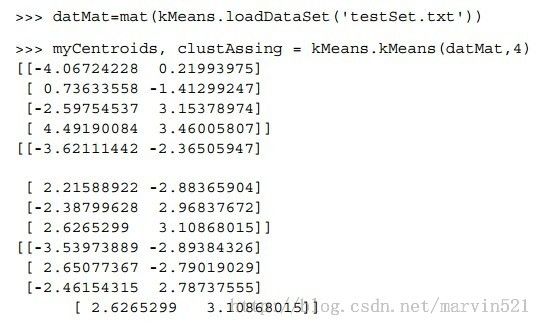
       代码也很简单，其中函数loadDataSet用来加载数据集，函数distEclud用来计算两个样本的距离，函数randCent为样本随机的分配K个质心（centroid）,另外注意一下样本的质心维度和样本维度是一样的，这个应该没有异议，高维空间中的坐标，最后函数kMeans则是k均值聚类算法的核心步骤，和原理都是一一对应的。下面是运行结果：

 

 

（图二）

        从（图二）可以看出质心的更新，不过按照k-means的聚类规则很容易陷入局部最小，陷入局部最小说简单的就是随机初始的质心分布的不是太好，最后迭代终止后，两个质心有可能在同一堆数据上，而另外一个质心成了另外两堆离的近样本的唯一质心（如下面图三所示）。说的复杂一些就是马尔科夫岁机场中配置的代价函数不是好的目标函数（虽然这里没写出这个函数）。为了解决这个问题，有人提出了二分K均值聚类算法，该算法也比较简单，首先把所有样本作为一个簇，然后二分该簇，接着选择其中一个簇进行继续进行二分。选择哪一个簇二分的原则就是能否使得误差平方和（SSE: Sum of Squared Error）进可能的小。也就是说该算法有了个好的目标函数，SSE的计算其实就是距离和。下面来看看二分K均值聚类算法的代码：

 

def biKmeans(dataSet, k, distMeas=distEclud):

    m = shape(dataSet)[0]

    clusterAssment = mat(zeros((m,2)))

    centroid0 = mean(dataSet, axis=0).tolist()[0]

    centList =[centroid0] #create a list with one centroid

    for j in range(m):#calc initial Error

        clusterAssment[j,1] = distMeas(mat(centroid0), dataSet[j,:])**2

    while (len(centList) < k):

        lowestSSE = inf

        for i in range(len(centList)):

            ptsInCurrCluster = dataSet[nonzero(clusterAssment[:,0].A==i)[0],:]#get the data points currently in cluster i

            centroidMat, splitClustAss = kMeans(ptsInCurrCluster, 2, distMeas)

            sseSplit = sum(splitClustAss[:,1])#compare the SSE to the currrent minimum

            sseNotSplit = sum(clusterAssment[nonzero(clusterAssment[:,0].A!=i)[0],1])

            print "sseSplit, and notSplit: ",sseSplit,sseNotSplit

            if (sseSplit + sseNotSplit) < lowestSSE:

                bestCentToSplit = i

                bestNewCents = centroidMat

                bestClustAss = splitClustAss.copy()

                lowestSSE = sseSplit + sseNotSplit

        bestClustAss[nonzero(bestClustAss[:,0].A == 1)[0],0] = len(centList) #change 1 to 3,4, or whatever

        bestClustAss[nonzero(bestClustAss[:,0].A == 0)[0],0] = bestCentToSplit

        print 'the bestCentToSplit is: ',bestCentToSplit

        print 'the len of bestClustAss is: ', len(bestClustAss)

        centList[bestCentToSplit] = bestNewCents[0,:].tolist()[0]#replace a centroid with two best centroids 

        centList.append(bestNewCents[1,:].tolist()[0])

        clusterAssment[nonzero(clusterAssment[:,0].A == bestCentToSplit)[0],:]= bestClustAss#reassign new clusters, and SSE

    return mat(centList), clusterAssment

 

 

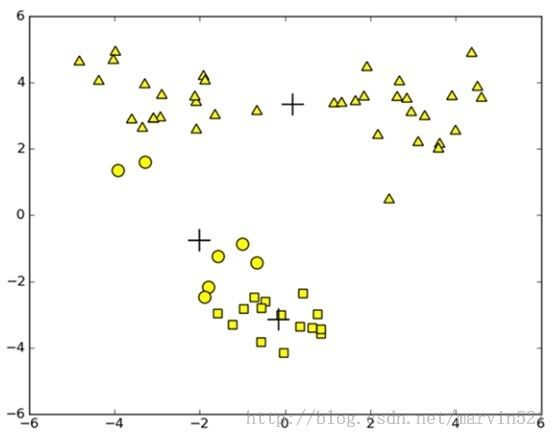
       这个算法比K均值聚类算法效果好一些，比如（图三）是K均值算法在随机初始化不好的情况下聚类的效果示意图：

 

（图三）

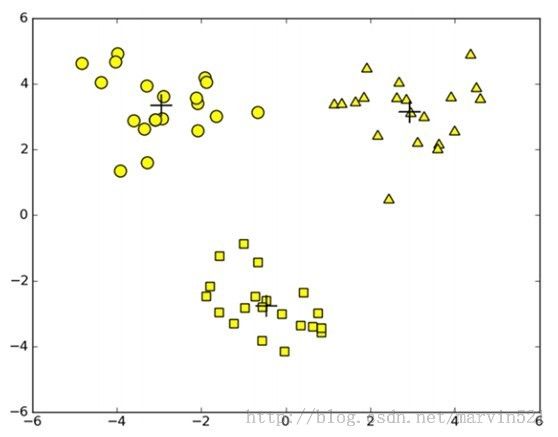
         而用二分K均值聚类跑出的效果图如（图四）所示：

 

（图四）

 

       到此为止，关于K均值的聚类算法也就说完了，虽然有二分K均值聚类算法改进了K均值聚类算法的不足，但也不是没缺点，它们的共同的缺点就是必须事先确定K的值，现实中的数据我们有可能不知道K的值，如何确定K的值也是学术界一直在研究的问题，现在常用的解决办法是用层次聚类（Hierarchical Clustering），或者借鉴下LDA中的话题聚类分析。最后多说一句：谱聚类也是图像中的一个大成员，用途很广，典型的就是图像分割。

 

 转载请注明来源：http://blog.csdn.net/marvin521/article/details/9674075

参考文献：

     [1] machine learning in action.Peter Harrington 

     [2] SpectralMatting.Anat Levin