有上下界的网络流问题
此类问题可以分为三小类问题:
一、无源汇有上下界最大流
二、有源汇有上下界最大流
三、有源汇有上下界最小流
1、无源汇有上下界最大流
题目链接: sgu194 Reactor Cooling
题目大意:给n个点,及m根pipe,每根pipe用来流躺液体的,单向的,每时每刻每根pipe流进来的物质要等于流出去的物质,要使得m条pipe组成一个循环体,里面流躺物质。并且满足每根pipe一定的流量限制,范围为[Li,Ri].即要满足每时刻流进来的不能超过Ri(最大流问题),同时最小不能低于Li。
解题思路:O(-1)。
建图模型: 以前写的最大流默认的下界为0,而这里的下界却不为0,所以我们要进行再构造让每条边的下界为0,这样做是为了方便处理。对于每根管子有一个上界容量up和一个下界容量low,我们让这根管子的容量下界变为0,上界为up-low。可是这样做了的话流量就不守恒了,为了再次满足流量守恒,即每个节点"入流=出流”,我们增设一个超级源点st和一个超级终点sd。我们开设一个数组du[]来记录每个节点的流量情况。
du[i]=in[i](i节点所有入流下界之和)-out[i](i节点所有出流下界之和)。
当du[i]大于0的时候,st到i连一条流量为du[i]的边。
当du[i]小于0的时候,i到sd连一条流量为-du[i]的边。
最后对(st,sd)求一次最大流即可,当所有附加边全部满流时(即maxflow==所有du[]>0之和),有可行解。
 View Code
View Code
1 #include <iostream> 2 #include <cstdio> 3 #include <cmath> 4 #include <algorithm> 5 #include <cstring> 6 using namespace std; 7 8 const int mn=22222; 9 const int mm=1000000; 10 const int oo=0x3fffffff; 11 int node, st, sd, edge, Edge; 12 int reach[mm], flow[mm], next[mm]; 13 int head[mn], work[mn], dis[mn], que[mn]; 14 int du[mm], ans[mm], id[mm], dn[mm]; 15 16 inline void init(int _node, int _st, int _sd) 17 { 18 node=_node, st=_st, sd=_sd; 19 for(int i=0; i<node; i++) 20 head[i]=-1; 21 edge=0; 22 } 23 24 inline void addedge(int u, int v, int c1, int c2, int ID) 25 { 26 id[edge]=ID, reach[edge]=v, flow[edge]=c1, next[edge]=head[u],head[u]=edge++; 27 id[edge]=0, reach[edge]=u, flow[edge]=c2, next[edge]=head[v],head[v]=edge++; 28 } 29 30 bool bfs() 31 { 32 int u, v, l=0, h=0; 33 for(int i=0; i<node; i++) dis[i]=-1; 34 que[l++]=st; 35 dis[st]=0; 36 while(l!=h) 37 { 38 u=que[h++]; 39 if(h==mn) h=0; 40 for(int i=head[u]; i>=0; i=next[i]) 41 { 42 v=reach[i]; 43 if(flow[i]&&dis[v]<0) 44 { 45 dis[v]=dis[u]+1; 46 que[l++]=v; 47 if(l==mn) l=0; 48 if(v==sd) return true; 49 } 50 } 51 } 52 return false; 53 } 54 55 int dfs(int u, int exp) 56 { 57 if(u==sd) return exp; 58 for(int &i=work[u]; i>=0; i=next[i]) 59 { 60 int v=reach[i], tp; 61 if(flow[i]&&dis[v]==dis[u]+1&&(tp=dfs(v,min(flow[i],exp)))>0) 62 { 63 flow[i]-=tp; 64 flow[i^1]+=tp; 65 return tp; 66 } 67 } 68 return 0; 69 } 70 71 void Dinic() 72 { 73 while(bfs()) 74 { 75 for(int i=0; i<node; i++) work[i]=head[i]; 76 while(dfs(st,oo)); 77 } 78 } 79 80 int main() 81 { 82 int n,m; 83 while(~scanf("%d%d",&n,&m)) 84 { 85 init(n+2,0,n+1); 86 for(int i=1; i<=m; i++) 87 { 88 int u, v, down, up; 89 scanf("%d%d%d%d",&u,&v,&down,&up); 90 addedge(u,v,up-down,0,i); 91 du[u]-=down; 92 du[v]+=down; 93 dn[i]=down; 94 } 95 Edge=edge; 96 for(int i=1; i<=n; i++) 97 { 98 if(du[i]>0) addedge(st,i,du[i],0,0); 99 if(du[i]<0) addedge(i,sd,-du[i],0,0); 100 } 101 Dinic(); 102 bool flag=true; 103 for(int i=head[st]; i>=0; i=next[i]) 104 if(flow[i]>0) 105 { 106 flag=false; 107 break; 108 } 109 if(!flag) puts("NO"); 110 else 111 { 112 puts("YES"); 113 for(int i=0; i<Edge; i++) ans[id[i]]=flow[i^1]; 114 for(int i=1; i<=m; i++) 115 printf("%d\n",ans[i]+dn[i]); 116 } 117 } 118 return 0; 119 }
2、有源汇有上下界的最大流
题目大意:一个屌丝给m个女神拍照,计划拍照n天,每一天屌丝最多个C个女神拍照,每天拍照数不能超过D张,而且给每个女神i拍照有数量限制[Li,Ri],对于每个女神n天的拍照总和不能超过Gi,如果有解求屌丝最多能拍多少张照,并求每天给对应女神拍多少张照;否则输出-1。
解题思路:增设一源点st,汇点sd,st到第i天连一条上界为Di下界为0的边,每个女神到汇点连一条下界为Gi上界为oo的边,对于每一天,当天到第i个女孩连一条[Li,Ri]的边。
建图模型:源点s,终点d。超级源点ss,超级终点dd。首先判断是否存在满足所有边上下界的可行流,方法可以转化成无源汇有上下界的可行流问题。怎么转换呢?
增设一条从d到s没有下界容量为无穷的边,那么原图就变成了一个无源汇的循环流图。接下来的事情一样,超级源点ss连i(du[i]>0),i连超级汇点(du[i]<0),
对(ss,dd)进行一次最大流,当maxflow等于所有(du[]>0)之和时,有可行流,否则没有。
当有可行流时,删除超级源点ss和超级终点dd,再对(s,d)进行一次最大流,此时得到的maxflow则为题目的解。为什么呢?因为第一次maxflow()只是求得所有满足下界的流量,而残留网络(s,d)路上还有许多自由流(没有和超级源点和超级汇点连接的边)没有流满,所有最终得到的maxflow=(第一次流满下界的流+第二次能流通的自由流)。
 View Code
View Code
1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <queue> 5 #include <algorithm> 6 using namespace std; 7 8 const int mn=2222; 9 const int mm=1000000; 10 const int oo=100000000; 11 int node, st, sd, edge; 12 int reach[mm], flow[mm], next[mm]; 13 int head[mn], work[mn], dis[mn], que[mn]; 14 int du[mn], dn[444][1111], id[444][1111]; 15 16 inline void init(int _node, int _st, int _sd) 17 { 18 node=_node, st=_st, sd=_sd; 19 for(int i=0; i<node; i++) 20 head[i]=-1, du[i]=0; 21 edge=0; 22 } 23 24 inline void addedge(int u, int v, int c1, int c2) 25 { 26 reach[edge]=v, flow[edge]=c1, next[edge]=head[u],head[u]=edge++; 27 reach[edge]=u, flow[edge]=c2, next[edge]=head[v],head[v]=edge++; 28 } 29 30 bool bfs() 31 { 32 int u, v, l=0, h=0; 33 for(int i=0; i<node; i++) dis[i]=-1; 34 que[l++]=st; 35 dis[st]=0; 36 while(l!=h) 37 { 38 u=que[h++]; 39 if(h==mn) h=0; 40 for(int i=head[u]; i>=0; i=next[i]) 41 { 42 v=reach[i]; 43 if(flow[i]&&dis[v]<0) 44 { 45 dis[v]=dis[u]+1; 46 que[l++]=v; 47 if(l==mn) l=0; 48 if(v==sd) return true; 49 } 50 } 51 } 52 return false; 53 } 54 55 int dfs(int u, int exp) 56 { 57 if(u==sd) return exp; 58 for(int &i=work[u]; i>=0; i=next[i]) 59 { 60 int v=reach[i], tp; 61 if(flow[i]&&dis[v]==dis[u]+1&&(tp=dfs(v,min(flow[i],exp)))>0) 62 { 63 flow[i]-=tp; 64 flow[i^1]+=tp; 65 return tp; 66 } 67 } 68 return 0; 69 } 70 71 int Dinic() 72 { 73 int max_flow=0, flow; 74 while(bfs()) 75 { 76 for(int i=0; i<node; i++) work[i]=head[i]; 77 while(flow=dfs(st,oo)) max_flow+=flow; 78 } 79 return max_flow; 80 } 81 82 int main() 83 { 84 int n, m, g, l, r, c, d; 85 while(scanf("%d%d",&n,&m)!=EOF) 86 { 87 init(n+m+2,n+m,n+m+1); 88 for(int i=0; i<m; i++) 89 { 90 scanf("%d",&g); 91 du[sd]+=g; 92 du[i+n]-=g; 93 addedge(i+n,sd,oo-g,0); 94 } 95 memset(id,0,sizeof(id)); 96 for(int i=0; i<n; i++) 97 { 98 scanf("%d%d",&c,&d); 99 addedge(st,i,d,0); 100 for(int j=0; j<c; j++) 101 { 102 scanf("%d%d%d",&g,&l,&r); 103 du[i]-=l; 104 du[g+n]+=l; 105 dn[i][g]=l; 106 addedge(i,g+n,r-l,0); 107 id[i][g]=edge-1; 108 } 109 } 110 addedge(sd,st,oo,0); 111 st=node, sd=node+1, node+=2; 112 head[st]=head[sd]=-1; ///!! 113 int sum=0; 114 for(int i=0; i<node-2; i++) 115 { 116 if(du[i]>0) sum+=du[i], addedge(st,i,du[i],0); 117 else addedge(i,sd,-du[i],0); 118 } 119 int maxflow=Dinic(); 120 if(maxflow!=sum) puts("-1"); 121 else 122 { 123 head[st]=head[sd]=-1, node-=2; 124 st=node-2, sd=node-1; 125 maxflow=Dinic(); 126 printf("%d\n",maxflow); 127 for(int i=0; i<n; i++) 128 { 129 for(int j=0; j<m; j++) 130 if(id[i][j]) 131 printf("%d\n",flow[id[i][j]]+dn[i][j]); 132 } 133 } 134 puts(""); 135 } 136 return 0; 137 }
3、有源汇有上下界的最小流
题目链接: sgu176 Flow construction
题目大意:有一个类似于工业加工生产的机器,起点为1终点为n,中间生产环节有货物加工数量限制,输出u v z c, 当c等于1时表示这个加工的环节必须对纽带上的货物全部加工(即上下界都为z),c等于0表示加工没有上界限制,下界为0,求节点1(起点)最少需要投放多少货物才能传送带正常工作。
解题思路:
1、du[i]表示i节点的入流之和与出流之和的差。
2、增设超级源点st和超级汇点sd,连(st,du[i](为正)),(-du[i](为负),sd)。 ///增设超级源点和超级汇点,因为网络中规定不能有弧指向st,也不能有流量流出sd
3、做一次maxflow()。
4、源点(Sd)和起点(St)连一条容量为oo的边。
5、再做一次maxflow()。
6、当且仅当所有附加弧满载时有可行流,最后答案为flow[(Sd->St)^1],St到Sd最大流就是Sd到St最小流。
建图模型:同样转换成先求无源汇有上下界的可行流,先添加一条d到s容量为无穷的边,这里求最小流很容易让人产生歧路,为什么呢?当所有边满足下界条件并且能量守恒时,这时候求得的最大流不就是最小流么。这样是错误了,我开始了在这揣测了良久。
下面来看个例子:
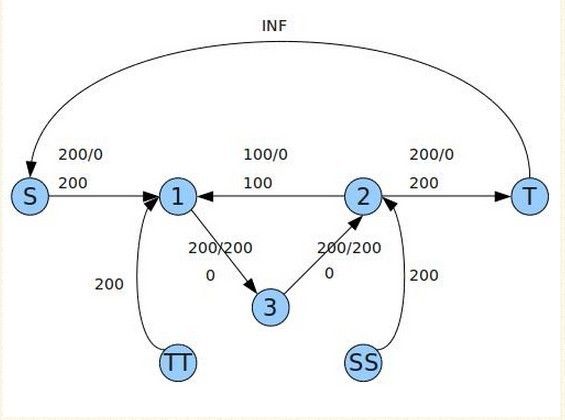



这样求得的最小流为200,而实际的可行最小流解只需100。
问题出在原图中存在环(循环流),而我们没有利用,导致流增大了。
解决方法:先不增加d->s容量为无穷的边,进行一次maxflow(),如果还没有满流,则加一条(d,s)容量为无穷的边,再进行一次maxflow(),当且仅当所有附加弧满载时,有可行解,解为flow[(d->s)^1](即d到s的后悔边权值)。
 View Code
View Code
1 #include <iostream> 2 #include <cstdio> 3 #include <cmath> 4 #include <algorithm> 5 #include <cstring> 6 using namespace std; 7 8 const int mn=111; 9 const int mm=11111; 10 const int oo=0x3fffffff; 11 int node, st, sd, edge, St, Sd, Edge; 12 int reach[mm], flow[mm], next[mm]; 13 int head[mn], work[mn], dis[mn], que[mn]; 14 int du[mm], ans[mm], id[mm], dn[mm]; 15 16 inline void init(int _node, int _st, int _sd) 17 { 18 node=_node, st=_st, sd=_sd; 19 for(int i=0; i<node; i++) 20 head[i]=-1, du[i]=0; 21 edge=0; 22 } 23 24 inline void addedge(int u, int v, int c1, int c2, int ID) 25 { 26 id[edge]=ID, reach[edge]=v, flow[edge]=c1, next[edge]=head[u],head[u]=edge++; 27 id[edge]=0, reach[edge]=u, flow[edge]=c2, next[edge]=head[v],head[v]=edge++; 28 } 29 30 bool bfs() 31 { 32 int u, v, l=0, h=0; 33 for(int i=0; i<node; i++) dis[i]=-1; 34 que[l++]=st; 35 dis[st]=0; 36 while(l!=h) 37 { 38 u=que[h++]; 39 if(h==mn) h=0; 40 for(int i=head[u]; i>=0; i=next[i]) 41 { 42 v=reach[i]; 43 if(flow[i]&&dis[v]<0) 44 { 45 dis[v]=dis[u]+1; 46 que[l++]=v; 47 if(l==mn) l=0; 48 if(v==sd) return true; 49 } 50 } 51 } 52 return false; 53 } 54 55 int dfs(int u, int exp) 56 { 57 if(u==sd) return exp; 58 for(int &i=work[u]; i>=0; i=next[i]) 59 { 60 int v=reach[i], tp; 61 if(flow[i]&&dis[v]==dis[u]+1&&(tp=dfs(v,min(flow[i],exp)))>0) 62 { 63 flow[i]-=tp; 64 flow[i^1]+=tp; 65 return tp; 66 } 67 } 68 return 0; 69 } 70 71 void Dinic() 72 { 73 int max_flow=0, flow; 74 while(bfs()) 75 { 76 for(int i=0; i<node; i++) work[i]=head[i]; 77 while(flow=dfs(st,oo)) max_flow+=flow; 78 } 79 } 80 81 int main() 82 { 83 int n, m; 84 while(~scanf("%d%d",&n,&m)) 85 { 86 init(n+1,1,n); 87 for(int i=1; i<=m; i++) 88 { 89 int u, v, c, k; 90 scanf("%d%d%d%d",&u,&v,&c,&k); 91 if(k) du[u]-=c, du[v]+=c, ans[i]=c; 92 else addedge(u,v,c,0,i); 93 } 94 St=st, Sd=sd, Edge=edge; 95 st=node, sd=node+1, node+=2; ///增设超级源点和超级汇点,因为网络中规定不能有弧指向st,也不能有流量流出sd 96 head[st]=head[sd]=-1; 97 for(int i=1; i<=n; i++) 98 { 99 if(du[i]>0) addedge(st,i,du[i],0,0); 100 if(du[i]<0) addedge(i,sd,-du[i],0,0); 101 } 102 Dinic(); 103 addedge(Sd,St,oo,0,0); 104 Dinic(); 105 bool flag=true; 106 for(int i=head[st]; i>=0; i=next[i]) 107 if(flow[i]>0) ///当且仅当附加弧达到满负载有可行流 108 { 109 flag=false; 110 break; 111 } 112 if(!flag) 113 puts("Impossible"); 114 else 115 { 116 int res=0, i; 117 for(i=head[Sd]; i>=0; i=next[i]) 118 if(reach[i]==St) break; 119 res=flow[i^1]; 120 printf("%d\n",res); 121 for(i=0; i<Edge; i++) ans[id[i]]=flow[i^1]; 122 for(i=1; i<=m; i++) 123 { 124 if(i!=m) printf("%d ",ans[i]); 125 else printf("%d\n",ans[i]); 126 } 127 } 128 } 129 return 0; 130 }
