leetcode_question_85 Largest Rectangle in Histogram

 

Given n non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

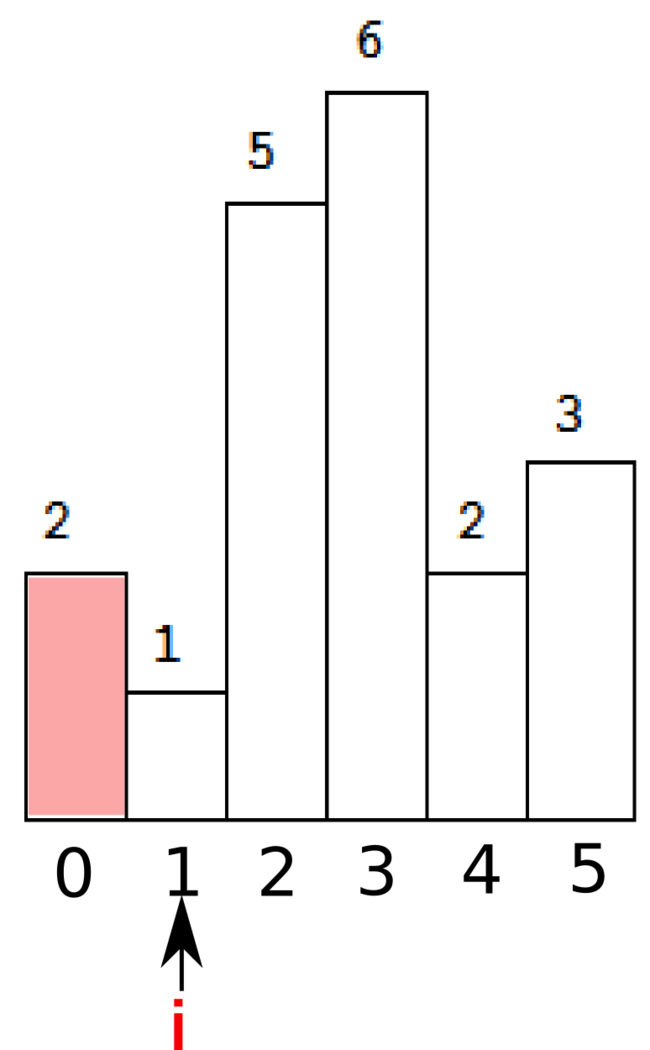
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

 

The largest rectangle is shown in the shaded area, which has area = 10 unit.

 

For example,
Given height = [2,1,5,6,2,3],
return 10.

O(n^2):

Judge Small: Accepted!
Judge Large: Time Limit Exceeded

 

int largestRectangleArea(vector<int> &height) {
        // Start typing your C/C++ solution below
        // DO NOT write int main() function
        int end = height.size();
    	int begin = 0;
		int largestarea = 0;
		for(int i = begin; i < end; ++i)
		{
			int area;
			int high = height[i];
			for(int j = i; j < end; ++j){
				if(height[j] < high) high = height[j];
				area = (j - i + 1)*high;
				if(area > largestarea) largestarea = area;
			}
		}
		return largestarea;
    }

 

O(n):

Judge Small: Accepted!
Judge Large:Accepted!

 

class Solution {
public:
    int Max(int a, int b){return a > b ? a : b;}
    int largestRectangleArea(vector<int> &height) {
    	height.push_back(0);
        stack<int> stk;
        int i = 0;
        int maxArea = 0;
        while(i < height.size()){
            if(stk.empty() || height[stk.top()] <= height[i]){
                stk.push(i++);
            }else {
                int t = stk.top();
				stk.pop();
                maxArea = Max(maxArea, height[t] * (stk.empty() ? i : i - stk.top() - 1));
            }
        }
        return maxArea;
    }
};

就用题目中的[2,1,5,6,2,3]来解释一下这段代码吧。

首先，如果栈是空的，那么索引i入栈。那么第一个i=0就进去吧。注意栈内保存的是索引，不是高度。然后i++。

然后继续，当i=1的时候，发现h[i]小于了栈内的元素，于是出栈。（由此可以想到，哦，看来stack里面只存放height单调递增的索引）

这时候stack为空，所以面积的计算是h[t] * i。t是刚刚弹出的stack顶元素。也就是蓝色部分的面积。

继续。这时候stack为空了，继续入栈。注意到只要是连续递增的序列，我们都要keep pushing，直到我们遇到了i=4，h[i]=2小于了栈顶的元素。

这时候开始计算矩形面积。首先弹出栈顶元素，t=3。即下图绿色部分。

接下来注意到栈顶的（索引指向的）元素还是大于当前i指向的元素，于是出栈，并继续计算面积，粉色部分。

最后，栈顶的（索引指向的）元素小于了当前i指向的元素，循环继续，入栈并推动i前进。直到我们再次遇到下降的元素，也就是我们最后人为添加的dummy元素0.

同理，我们计算栈内的面积。由于当前i是最小元素，所以所有的栈内元素都要被弹出并参与面积计算。

注意我们在计算面积的时候已经更新过了maxArea。

总结下，我们可以看到，stack中总是保持递增的元素的索引，然后当遇到较小的元素后，依次出栈并计算栈中bar能围成的面积，直到栈中元素小于当前元素。

可以这样理解这个算法，看下图。

例如我们遇到最后遇到一个递减的bar（红色）。高度位于红线上方的（也就是算法中栈里面大于最右bar的）元素，他们是不可能和最右边的较小高度bar围成一个比大于在弹栈过程中的矩形面积了（黄色面积），因为红色的bar对他们来说是一个短板，和红色bar能围成的最大面积也就是红色的高度乘以这些“上流社会”所跨越的索引范围。但是“上流社会”的高度个个都比红色bar大，他们完全只计算彼此之间围成的面积就远远大于和红色bar围成的任意面积了。所以红色bar是不可能参与“上流社会”的bar的围城的。因为虽然长度不占优势，但是团结的力量是无穷的。它还可以参与“比较远的”比它还要屌丝的bar的围城。他们的面积是有可能超过上流社会的面积的，因为距离啊！所以弹栈到比红色bar小就停止了。

另外一个细节需要注意的是，弹栈过程中面积的计算。

h[t] * (stack.empty() ? i : i - stack.top() - 1)

h[t]是刚刚弹出的栈顶端元素。此时的面积计算是h[t]和前面的“上流社会”能围成的最大面积。这时候要注意哦，栈内索引指向的元素都是比h[t]小的，如果h[t]是目前最小的，那么栈内就是空哦。而在目前栈顶元素和h[t]之间（不包括h[t]和栈顶元素），都是大于他们两者的。如下图所示：

那h[t]无疑就是Stack.top()和t之间那些上流社会的短板啦，而它们的跨越就是i - Stack.top() - 1。

所以说，这个弹栈的过程也是维持程序不变量的方法啊：栈内元素一定是要比当前i指向的元素小的。