【路径规划】基于D*算法的移动机器人路径规划（Matlab代码实现）

 欢迎来到本博客❤️❤️❤️

博主优势：博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

​

⛳️座右铭：行百里者，半于九十。

目录

1 概述

2 A*算法

‍3 运行结果

4 参考文献

‍5 Matlab代码实现

---

1 概述

     智能导航是移动机器人的关键技术，在移动机器人的应用研究中具有重要地位1。导航主要由构建地图、定位和路径规划三部分构成。.地图构建是指移动机器人根据自身传感器感知周围的环境信息,建立其工作环境模型的过程;定位是指确定移动机器人在其工作环境中的具体位置的过程，即移动机器人在虚拟地图中的坐标和姿态;路径规划是指在复杂的环境中,在满足一定的约束条件下,如行走路径的长度短,路径的代价低、时间短等,找到一条从指定起始位置到指定目标位置的安全、无碰撞的优化路径。对于以上问题,在近几十年的研究中出现了多种有效的解决方案,如:同步建图与地图构建(SLAM)、蒙特卡洛定位算法3动态窗口算法(DWA)等等。

       DWA算法是机器人根据传感器获取局部信息的更新,实时控制机器人速度在一个有效的“窗口”内,完成机器人的局部路径规划。

D*算法是基于A*算法基础上提出的,对缺少环境先验信息或者对动态环境下的路径规划解决方案。

一、移动机器人路径规划概述

• 移动机器人在现代社会有着广泛的应用，如工业生产中的物流运输、家庭中的扫地机器人等。而路径规划是其智能导航的关键部分，直接影响机器人能否高效、安全地到达目标位置。路径规划的目的是在满足一定约束条件（如路径长度短、代价低、时间短等）的情况下，找到一条从起始位置到目标位置的安全、无碰撞的优化路径。在路径规划研究中，已经出现了多种算法，如A算法、Dijkstra算法等，D算法也是其中重要的一种。[1][2]

二、D*算法的基本原理

• 1. 基于A*算法的改进

  • D算法是基于A算法发展而来的。A算法是一种典型的启发式搜索算法，它通过选择合适的估价函数指导搜索朝着最有希望的方向前进以求得最优解，减少了无效搜索路径，提高了搜索效率。然而，A算法在缺少环境先验信息或者动态环境下存在一定局限性。D*算法正是针对这些情况的解决方案。[2]

  • 估价函数的调整：D算法在A算法的基础上，对估价函数进行了改进，使其能够更好地适应环境信息的变化。在D*算法中，会根据机器人周围环境的动态变化（如出现新的障碍物或者原有障碍物的移除）重新计算路径，这一过程中，估价函数会根据新的环境信息进行调整，从而保证机器人能够规划出可行的路径。

• 2. 应对动态环境

  • 在实际应用场景中，移动机器人所处的环境往往是动态变化的。例如在物流仓库中，货物的堆放位置可能随时改变，这就相当于出现了新的障碍物或者改变了原有的可通行区域。D算法能够有效地应对这种动态环境。当环境发生变化时，D算法不需要重新进行全局路径规划，而是可以利用之前的路径规划结果，通过局部调整快速地重新规划出一条可行的路径，大大减少了计算量和规划时间。

三、D*算法的实现步骤

• 1. 地图表示

  • 首先需要对移动机器人的工作环境进行建模，通常采用栅格地图来表示。在栅格地图中，将环境划分为一个个的小栅格，每个栅格可以表示为可通行区域、障碍物或者未知区域。这样的表示方式便于D*算法进行路径搜索和规划。

• 2. 初始化

  • 对算法中的相关参数进行初始化，如起始点、目标点、每个栅格的初始状态（如成本值等）等。同时，还需要建立一个用于存储搜索过程中相关信息的数据结构，如开放列表和关闭列表等。开放列表用于存储待扩展的节点，关闭列表用于存储已经扩展过的节点。

• 3. 搜索过程

  • 从起始点开始，根据估价函数计算周围节点的优先级，选择优先级最高的节点进行扩展。在扩展节点的过程中，会更新节点的成本值（包括从起始点到该节点的实际成本和到目标点的估计成本），并将新的节点加入开放列表。重复这个过程，直到找到目标点或者确定不存在可行路径。

• 4. 路径回溯

  • 当找到目标点后，通过从目标点回溯到起始点的方式确定最终的路径。在回溯过程中，会选择成本值最小的相邻节点，最终形成从起始点到目标点的路径。

四、D*算法与其他算法的比较

• 1. 与A*算法比较

  • 虽然D算法基于A算法发展而来，但在应对动态环境方面有着明显的优势。A算法在环境发生变化时，往往需要重新进行全局路径规划，而D算法只需要进行局部调整。在计算效率上，对于动态环境下的路径规划，D算法通常比A算法更高效。

• 2. 与Dijkstra算法比较

  • Dijkstra算法是一种贪心算法，它通过计算每个节点的距离来确定下一步的移动方向，最终找到最短路径。但是，Dijkstra算法在搜索过程中会搜索所有的节点，计算量较大。相比之下，D算法利用估价函数和启发式搜索，能够更快地找到可行路径，尤其是在复杂的动态环境中，D算法的优势更加明显。

五、D*算法在移动机器人路径规划中的应用案例

• 1. 仓储物流机器人

  • 在仓储物流场景中，机器人需要在货架之间穿梭搬运货物。环境中货物的堆放位置经常变化，属于典型的动态环境。采用D*算法，物流机器人能够快速地根据环境变化重新规划路径，提高货物搬运的效率，减少运输时间。

• 2. 未知环境探索机器人

  • 当机器人被用于探索未知环境（如外星探索或者地下洞穴探索）时，环境信息是逐步获取的，且可能随时遇到新的障碍物。D*算法可以根据不断获取的新环境信息及时调整路径规划，保证机器人能够持续朝着目标方向前进，提高探索任务的成功率。

六、D*算法的局限性与改进方向

• 1. 局限性

  • 尽管D算法在应对动态环境方面表现出色，但在一些复杂的、高度动态的环境下，可能会出现局部最优解的问题。例如，当环境中障碍物的变化频率非常高且变化范围较大时，D算法可能会陷入局部最优路径，无法找到全局最优路径。

  • D*算法的计算复杂度在一定程度上仍然较高，尤其是在大规模地图或者复杂环境下，可能会导致较长的规划时间，影响机器人的实时性操作。

• 2. 改进方向

  • 为了解决局部最优解的问题，可以考虑结合其他算法（如模拟退火算法等随机化算法）对D算法进行改进。模拟退火算法具有跳出局部最优解的能力，将其与D算法相结合，可以提高D*算法在复杂动态环境下找到全局最优解的概率。

  • 针对计算复杂度较高的问题，可以对算法进行优化，如采用更高效的数据结构来存储和处理地图信息，或者采用并行计算技术来提高计算速度，从而减少规划时间，提高机器人的实时响应能力。

2 A*算法

       A*算法是人工智能中一种典型的启发式搜索算法。通过选择合适的估价函数指导搜索朝着最有希望的方向前进以求得最优解。A*算法针对以往路径规划问题中常常产生的大量无效搜索路径,根据启发函数提高了收索的目的性,提高了算法的搜索效率。A*算法的设计核心是其估价函数。

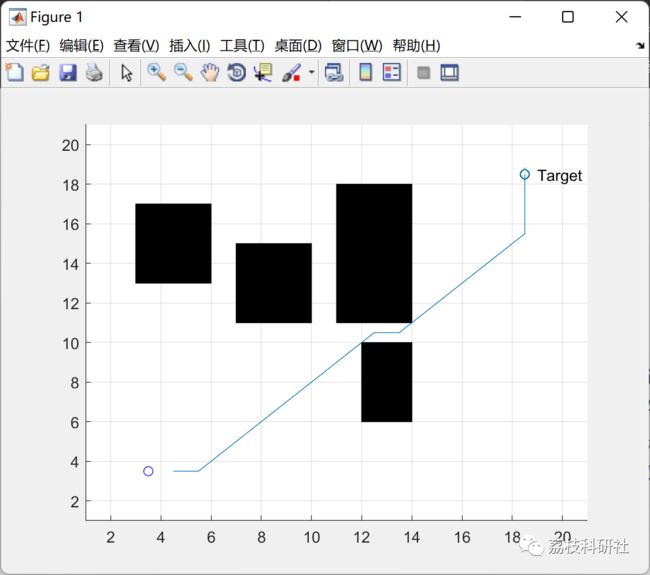
‍3 运行结果

部分代码：

clc
clear
close all

max_x=20;
max_y=20;

environment=2*(ones(max_x,max_y));

j=0;
x_val = 1;
y_val = 1;
axis([1 max_x+1 1 max_y+1])
grid on;
hold on;
n=0;

xval=18;
yval=18;
x_target=xval;
y_target=yval;

environment(xval,yval)=0;%Initialize environment with location of the target
plot(xval+.5,yval+.5,'gd');
text(xval+1,yval+.5,'Target')

% obstacle 1
for i = 3:5
    for j = 13:16
        environment(i,j) = -1; 
        %plot(i+.5,j+.5,'rd'); 
    end
end
x = [3, 6, 6, 3];
y = [13, 13, 17, 17];

fill(x,y,'k');
% obstacle 2
for i = 7:9
    for j = 11:14 
        environment(i,j) = -1;
        %plot(i+.5,j+.5,'rd'); 
    end
end

x = [7, 10, 10, 7];
y = [11, 11, 15, 15];

fill(x,y,'k');

% obstacle 3
for i = 11:13
    for j = 11:17 
        environment(i,j) = -1;
        %plot(i+.5,j+.5,'rd'); 
    end
end
x = [11, 14, 14, 11];
y = [11, 11, 18, 18];

fill(x,y,'k');
% obstacle 4
for i = 12:13
    for j = 6:9 
        environment(i,j) = -1;
        %plot(i+.5,j+.5,'rd'); 
    end
end

x = [12, 14, 14, 12];
y = [6, 6, 10, 10];

fill(x,y,'k');

% % obstacle 5
% for i = 15:16
%     for j = 6:17 
%         environment(i,j) = -1;
%         %plot(i+.5,j+.5,'rd'); 
%     end
% end
% 
% x = [15, 17, 17, 15];
% y = [6, 6, 18, 18];
% 
% fill(x,y,'k');

%plot(19+.5,19+.5,'gd');

xval=3;
yval=3;
x_start=xval;%Starting Position
y_start=yval;%Starting Position

environment(xval,yval)=1;
 plot(xval+.5,yval+.5,'bo');

valid=[]; % x | y | parent_x | parent_y | h(n) | g(n) | f(n) 

in_valid=[]; % x | y

k=1;
for i=1:max_x
    for j=1:max_y
        if(environment(i,j) == -1) % check if obstacle
            in_valid(k,1)=i; 
            in_valid(k,2)=j; 
            k=k+1;
        end
    end
end
in_valid_size=size(in_valid,1);

cell_x=x_start;
cell_y=y_start;
valid_size=1; % initialize size of valid_list
path_cost=0;
goal_distance=sqrt((cell_x-x_target)^2 + (cell_y-y_target)^2);

new_row=[1,8];
new_row(1,1)=1;
new_row(1,2)=cell_x;
new_row(1,3)=cell_y;
new_row(1,4)=cell_x; % parent x
new_row(1,5)=cell_y; % parent y 
new_row(1,6)=path_cost; % h
new_row(1,7)=goal_distance; % g
new_row(1,8)=goal_distance; % f

valid(valid_size,:)=new_row; % initializing path with start position
valid(valid_size,1)=0;

in_valid_size=in_valid_size+1;
in_valid(in_valid_size,1)=cell_x; % make it invalid for further iterations
in_valid(in_valid_size,2)=cell_y;

path_not_found=1;
obstacle_was_detected = 0;

% disp('Valid in the beginning');
% valid
% disp('In valid in the beginning');
% in_valid

while 1 % it will be broke only if no new obstacle gets detected just like in A* 

while((cell_x ~= x_target || cell_y ~= y_target) && path_not_found == 1)
    % x | y | h | g | f
    if obstacle_was_detected == 1
        fprintf('Value of cell x : %d celly : %d\n',cell_x,cell_y);
    end
    fprintf('Value of cell x : %d celly : %d\n',cell_x,cell_y);
    successors=explore_successors(cell_x,cell_y,path_cost,x_target,y_target,in_valid,max_x,max_y);
    successors_size=size(successors,1);
    for i=1:successors_size
    flag=0;
    for j=1:valid_size
        if(successors(i,1) == valid(j,2) && successors(i,2) == valid(j,3) ) % if successor same as already existing cell inpath
%             disp('valid')
%             valid
%             disp(' ');
            valid(j,8)=min(valid(j,8),successors(i,5)); % check for minimum f and then pick it 
            if valid(j,8) == successors(i,5)
                valid(j,4)=cell_x;% parent x
                valid(j,5)=cell_y;% parent y
                valid(j,6)=successors(i,3); % h
                valid(j,7)=successors(i,4); % g
            end;
            flag=1;
        end;
    end;
    if flag == 0 % if new cell with minimum f(n) then add to valid_path
        valid_size= valid_size+1;
        new_row=[1,8];
        new_row(1,1)=1;
        new_row(1,2)=successors(i,1);
        new_row(1,3)=successors(i,2);
        new_row(1,4)=cell_x; % parent x
        new_row(1,5)=cell_y; % parent y
        new_row(1,6)=successors(i,3); % h
        new_row(1,7)=successors(i,4); % g
        new_row(1,8)=successors(i,5); % f
        valid(valid_size,:)= new_row;
     end;
    end;

    index_min_cell = min_f(valid,valid_size,x_target,y_target);
    if (index_min_cell ~= -1) % if index with minimum fn is obstacle no path exists    
        cell_x=valid(index_min_cell,2);
        cell_y=valid(index_min_cell,3);
        path_cost=valid(index_min_cell,6);

        in_valid_size=in_valid_size+1; % put the cell in_valid so we dont come back on it again
        in_valid(in_valid_size,1)=cell_x;
        in_valid(in_valid_size,2)=cell_y;
        valid(index_min_cell,1)=0;
        %valid
        %in_valid
    else
        path_not_found=0;
    end;
end;

% backtracking to find the path

i=size(in_valid,1);
path=[];
xval=in_valid(i,1); % pick last in in_valid_list that must be target
yval=in_valid(i,2);
i=1;
path(i,1)=xval;
path(i,2)=yval;
i=i+1;

if ( (xval == x_target) && (yval == y_target))
    % obstacle 5
%     tappi = size(in_valid,1) + 1;
%     for p = 15:16                 %11:13 % w.r.t obstacle 3
%         for q = 6:17              %11:17 
%             environment(p,q) = -1;
%             in_valid(tappi,1) = p;
%             in_valid(tappi,2) = q;   
%             tappi = tappi + 1;
%             %plot(i+.5,j+.5,'rd'); 
%         end
%     end
%     in_valid_size= size(in_valid,1);
%     x = [15, 17, 17, 15];
%     y = [6, 6, 18, 18];
    %     x = [11, 14, 14, 11]; % with respect to obstacle 3
    %     y = [11, 11, 18, 18];

   fill(x,y,'k');    
   inode=0;
   parent_x=valid(find((valid(:,2) == xval) & (valid(:,3) == yval),1),4);
   parent_y=valid(find((valid(:,2) == xval) & (valid(:,3) == yval),1),5);
   
   while( parent_x ~= x_start || parent_y ~= y_start)
           path(i,1) = parent_x;
           path(i,2) = parent_y;
           
           inode=find((valid(:,2) == parent_x) & (valid(:,3) == parent_y),1);
           parent_x=valid(inode,4);
           parent_y=valid(inode,5);
           i=i+1;
    end;
 % plottin path
 obstacle_was_detected = 0;
 j=size(path,1);
 p=plot(path(j,1)+.5,path(j,2)+.5,'bo');
 %j=j-1;
 for i=j:-1:1
     
  pause(.25);
  fprintf('Path X : %d Y : %d\n',path(i,1),path(i,2));
  
  % -------------------------check if environment is altered ------------- 
  if environment(path(i,1),path(i,2)) == -1 
      
    disp ('obstacle detected');
    if(obstacle_was_detected == 0)
        
        % we will start computing the path from the parent path where
        % obstacle was first foun
        cell_x = valid(find((valid(:,2) == path(i,1)) & (valid(:,3) == path(i,2)),1),4); 
        cell_y=valid(find((valid(:,2) == path(i,1)) & (valid(:,3) == path(i,2)),1),5);
        path_cost=valid(find((valid(:,2) == path(i,1)) & (valid(:,3) == path(i,2)),1),6);
   
    end
    
    obstacle_was_detected = 1;
    
    % remove obstacles from valid list
    [valid, valid_size] = remove(valid,path(i,1),path(i,2));
    valid = increase_f(valid,path(i,1), path(i,2),in_valid,max_x,max_y);
    
    %disp('Valid after increasing');
    %valid
    
  elseif obstacle_was_detected == 0 
      
    set(p,'XData',path(i,1)+.5,'YData',path(i,2)+.5);
    drawnow ;
    
  else
%     fprintf('Removing X : %d Y : %d from invalid\n',path(i,1),path(i,2));
%     [x, y] = size(in_valid);
%     fprintf('Initial Size : %d x %d\n', x,y);

    in_valid(find((in_valid(:,1) == path(i,1)) & (in_valid(:,2) == path(i,2)),1),:) = [];
    
%     [x, y] = size(in_valid);
%     fprintf('Final Size : %d x %d\n', x,y);

    valid = increase_f(valid,path(i,1), path(i,2),in_valid,max_x,max_y); % updating costs
    
  end
  
 end
 if obstacle_was_detected == 0
     
    plot(path(:,1)+.5,path(:,2)+.5);
    break
    
 else
     
     continue
     
 end
 
else
    
    disp( 'Sorry, No path exists to the Target!');
    break
    
end

end
 

4 参考文献

[1]张希闻,肖本贤.改进D~*算法的移动机器人路径规划[J].传感器与微系统,2018,37(12):52-54+58.DOI:10.13873/J.1000-9787(2018)12-0052-03.

[1]张贺,胡越黎,王权,燕明.基于改进D*算法的移动机器人路径规划[J].工业控制计算机,2016,29(11):73-7477

‍5 Matlab代码实现