计算几何之凸包_卷包裹算法

====================================================================

一.凸集&凸包

(下文中所有的集合 若不作特殊说明 都是指欧氏空间上的集合)

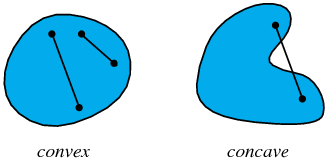
凸集(Convex Set):任意两点的连线都在这个集合内的集合就是一个凸集.

A set in Euclidean space  is convex set if it contains all the line segments connecting any pair of its points.

http://mathworld.wolfram.com/Convex.html

凸包(Convex Hull):包含集合S的所有凸集的交集就是集合S的凸包.

The convex hull of a set of points S in N dimensions is the intersection of all convex sets containing S.

                                

我们经常关注一个点集的凸包 这也是计算几何学的一个基本问题

我们现在已经有成熟的算法可以求出平面点集的凸包和空间点集的凸包

甚至有的算法可以方便的求出任意维度欧氏空间内的一个点集的凸包

凸包有着优美而实用的性质 我们可以利用凸包把一个杂乱的点集所包含的信息进行有效的概括 梳理

====================================================================

二.平面点集的凸包的算法

(下文中所有凸包 若不作特殊说明 都是指平面点集的凸包)

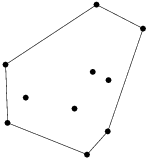
有两种直观的理解凸包的方式

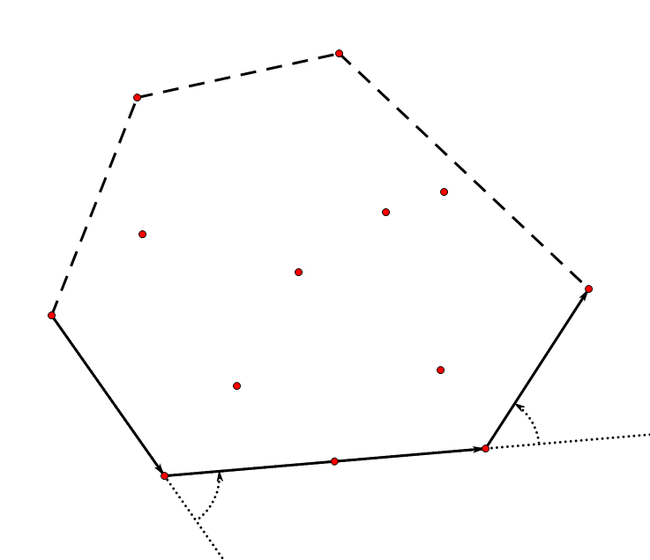
在木板上钉钉子 用一个有弹性的橡皮筋去框住所有钉子

橡皮筋形成的图形就是这个钉子所构成的点集的凸包

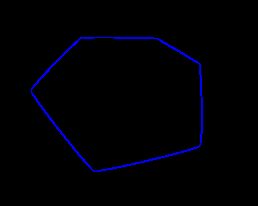
还有一种理解我们用一根麻绳绑住一个外面的钉子 然后拉着麻绳绕所有钉子一圈

这个麻绳最后也构成了点集的凸包

其中 第二种理解是我们一个经典算法 卷包裹法(Gift Wrapping)的思路

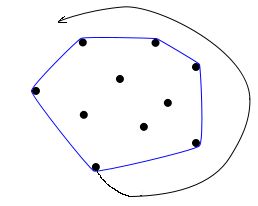
卷包裹算法从一个必然在凸包上的点开始向着一个方向依次选择最外侧的点

当回到最初的点时 所选出的点集就是所要求的凸包

这里还有两个问题不是很清楚:

1.怎么确定一个肯定在凸包上的点?

这个问题很好解决 取一个最左边的也就是横坐标最小的点

如果有多个这样的点 就取这些点里 纵坐标最小的

这样可以很好的处理共线的情况

2.如何确定下一个点(即最外侧的点)?

我们需要利用向量的叉积来解决这个问题

-----------------------------------------------------------------------

向量的叉积(Cross Product)原本是三维空间中的问题 在二维中也有巧妙的应用

http://mathworld.wolfram.com/CrossProduct.html

(下文中所有的叉积 若不作特殊说明 都是指二维中新定义的叉积

下文中所有的向量乘法 若不作特殊说明 都是指向量的叉积)

我们定义二维向量<x1,y1>和<x2,y2>的叉积为一个实数Cp=x1*y2-x2*y1

叉积有两条性质很常用 也很好用

1.叉积的一半是一个三角形的有向面积

这个公式可以避免面积计算的误差 如果点是整点 那么所有运算都是整数

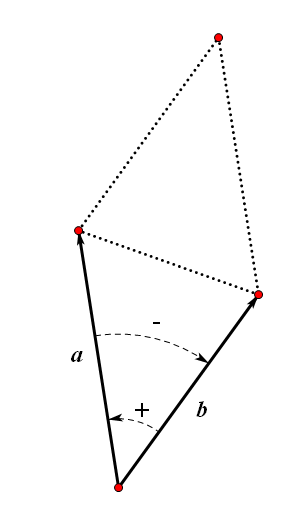
2.向量的叉积的符号代表着向量旋转的方向

向量的叉积是不满足交换律的

向量A乘以向量B 如果为正则为A逆时针旋转向B 否则为顺时针

当然这里A转向B的角总是考虑一个小于180度以内的角 否则就会出错

-----------------------------------------------------------------------

有了向量 我们就可以选取一个最外侧的点了

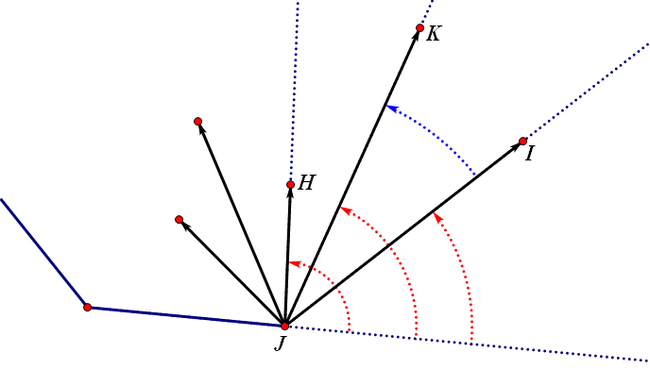
比如现在我们卷包裹卷到J点我们要选取一个最外侧的点

当然比较红色的到角可以直接得到最外侧的点 不过不方便

我们可以考虑那个蓝色的到角

利用向量 我们可以比较哪个点"更外侧"

比如点K和点I 我们利用向量JK乘以向量JI得到一个数 这个数应该是负数 说明I比K更外侧

两个向量的比较具有传递性 所以我们可以像N个数里取最大的数一样取出最外侧的

遍历所有点 每个点都和现有最外侧的点比较 得到新的最外侧的点

至此两个问题都得以解决 我们可以写出满足一般要求的卷包裹算法了

不过还遗留有一个问题 就是处理共线的问题

有时候我们需要凸包边上的点也考虑到 有时候却需要去掉这些点

我们通常称在凸包顶点处的点为极点

如果我们只要求保留极点而去除在边上的点

我们只需在取外侧的点的时候 碰到共线的点取最远的

相反 如果我们要保留所有在边上的点我们只需要在共线的点中取最近的

这样整个卷包裹法终于完成了

给出完整的代码:

poj  1696 Space Ant

#include <iostream>
#include <cstdio>
#include<cstring>
using namespace std;
#define N 100
struct node{
	int x,y,id,tag;
}ant[N],point;
int crossproduct(node a,node b,node c){
	return (a.x-c.x)*(b.y-c.y)-(a.y-c.y)*(b.x-c.x);
}
int dist(node a,node b){
	return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y);
}
int main(int argc, char** argv) {
	int n,m,i,ans[N],k,tmp;
	scanf("%d",&m);
	while(m--){
		k=0;
		point.x=0xfffff;
		point.y=0xfffff;
		scanf("%d",&n);
		for(i=0;i<n;i++){
			scanf("%d%d%d",&ant[i].id,&ant[i].x,&ant[i].y);
			ant[i].tag=0;
			if(ant[i].y<point.y||ant[i].y==point.y&&ant[i].x<point.x){
				tmp=i;
				point.x=ant[i].x;
				point.y=ant[i].y;
			}
		}
		ant[tmp].tag=1;
		ans[k++]=tmp;
		while(k!=n){
			for(i=0;i<n;i++)
				if(!ant[i].tag){
					tmp=i;
					break;
				}
			for(i=0;i<n;i++){
				if(i==tmp||ant[i].tag)
					continue;
				if(crossproduct(ant[tmp],ant[i],ant[ans[k-1]])<0||
				crossproduct(ant[tmp],ant[i],ant[ans[k-1]])==0&&
				dist(ant[i],ant[ans[k-1]])<dist(ant[tmp],ant[ans[k-1]])){
					tmp=i;
				}
				
			}
			ant[tmp].tag=1;
			ans[k++]=tmp;
		}
		printf("%d",k);
		for(i=0;i<k;i++)
			printf(" %d",ant[ans[i]].id);
		printf("\n");
	}
	return 0;
}

还有两点要补充说明一下:

1.卷包裹算法的复杂度是O(NH)

N是全部的点数 H是最终在凸包上的点数

所以卷包裹算法很适合凸包上的点很少的时候 通常随机数据很快

但是构造出的凸包上的点很多的数据 这个算法就会很慢

比如所有的点都在一个圆周上

2.卷包裹算法输出的点是有序的

这也是对二维凸包算法的一个基本要求

通常只有保证有序才能进行进一步的计算

通过改变CMP函数可以改变上文中提到的共线(取/不取)以及这里的序(顺时针/逆时针)的问题

====================================================================