投资组合风险管理

金融风险是与金融有关的风险，比如金融市场风险、金融产品风险和金融机构风险等，如果按照风险来源不同，则可以分为信用风险、市场风险、操作风险和流动性风险等。

市场风险

约翰·赫尔认为（2018）对于市场风险度量理论主要有四种方法，

• 第一，均值—方差模型：如果方差波动越大，收益率波动越大，面临的风险越大；
• 第二，β系数法：诞生于 CAPM 模型，将 β 值与 1 比较，若大于 1 则该产品大于市场风险，若小于 1 则是该产品小于市场风险；
• 第三，缺口模型：主要分为敏感性缺口模型和持续期缺口模型，该模型主要是对利率风险度量，假如缺口越大，金融风险就越大；
• 第四，VaR 法（即在险价值）：在正常的条件下，若给定置信水平和给定的时间区间，某项资产或者资产组合预期可能发生的最大损失。

信用风险

对于信用风险度量理论，主要有两种方法，

• 第一，传统定性分析。比如 5C信用评级法，信用评级法主要对评级客户的品质（character）、能力（capacity）、资本（capital）、抵押（collateral）以及条件（condition）五个方面进行评估，目的就是从五个方面进行评估，从而获得客户信用违约风险的大小，该种评估一般由是专门的评级机构对客户进行评级；
• 第二，现代定量分析，比如KMV模型和信用度量组合模型。前者是用于估计借款企业的违约率，后一个是估算信用资质量变化而导致的组合价值波动情况及价值的分布状况，计算信用资产组合的在险价值的方法。

流动性风险

对于流动性风险度量理论，包括融资流动性风险衡量和资产流动性衡量，资产流动性风险度量主要有两种方法，

• 第一，买卖价差法:利用市场同一交易标的在同一时间买入和卖出价格之差衡量流动性风险的一种方法；第二，冲击成本，指交易中迅速而且大规模地买进或者卖出证券，不能按照预定价位而多支出地成本，市场流动性越高，冲击成本越低，市场流动性越低，冲击成本越高。

风险指标

资产组合理论、资本资产定价模型（CAPM 模型）和股票价格行为理论是20 世纪 60 年代开始产生的，三者是现代投资组合业绩评价的基础，在这三者基础之上也衍生的投资组合业绩评价方法，

Treynor、Sharpe 和 Jensen 提出的三大经典风险调整收益度量，

• 其中 Treynor 指数是 Treynor 在 1965 年提出将投资组合中引入系统性风险因子 β，来衡量投资组合由于单位风险所产生的超额收益，如果 β 值越大，说明在同样的风险下投资组合所获得的超额收益就会越高，投资组合相对而言其业绩越好；
• Sharpe（1966）随后提出 Sharpe 指数将投资组合收益率的标准差作为系统性风险，从而计算出单位风险所获得的超额收益，与Treynor 指数一样，数值越大代表投资组合的业绩越好；
• 1968 年 Jensen 接下来又提出了 Jensen 指数，是基于 CAMP 模型提出了新的风险调整收益度量法，Jensen 指数指的是投资组合的实际收益率与证券市场上组合期望收益率之差，这个差值越高说明业绩越好，至今为止，Jensen 指数是应用最多的业绩评价指标之一，现有的大部分业绩归因模型也是参照 Jensen 指数构建出来的。

衡量风险的方法有很多种
。Beta是一种将投资的风险或波动性与一般市场进行比较的衡量标准。标准差衡量投资平均绩效的分散程度。夏普比率衡量投资回报是否公平地补偿投资者承担的相关风险水平。

收益率波动率

收益波动率代表各期收益率与平均收益率的偏离或者聚合程度，等于收益率的标准差，也等于方差的平方根，如果收益波动率值越大，不确定性和风险就越高。
更常使用的是年化波动率，年化方式是将波动率*，其中252为一年的交易天数。

最大回撤

最大回撤率是指在选定周期内任一历史时点往后推，产品净值走到最低点时的收益率回撤幅度的最大值。具体的计算方式在指标的定义中已经给出。
最大回撤用来描述买入产品后可能出现的最糟糕的情况。
由于该指标更加直观地表现了风险，因此基金投资者对最大回撤指标的关注一般要高于波动率。

$\text{Max Drawdown}=\frac{\text{Max}(P_x-P_y)}{P_x}$

$\alpha$（詹森指数），$\beta$

根据单指数定价模型，基金的收益率可以表示为

$$R_P=\alpha +\beta R_B+\epsilon$$

其中为$R_P$基金收益率，$R_B$为基准收益率，$\alpha$和$\beta$为回归系数，$\epsilon$为扰动项。
将基金收益率与比较基准的收益率按照该模型线性回归后，即可得到$\alpha$和$\beta$的值。
$\beta$是一种风险系数，用来衡量基金相对于基准的波动情况，值越大说明风险越高。
贝塔系数衡量的是单个资产或行业相对于整个股票市场的系统风险程度。
市场始终是一项投资的贝塔基准，而市场的贝塔始终为1。
资产的贝塔值等于1，则该资产的波动性特征与大盘完全相同。
贝塔值大于1的资产意味着它比市场更不稳定。
贝塔系数小于1的资产意味着其波动性低于市场。
当将一项投资与整个市场进行比较时，贝塔值最有用。Beta的计算方法是将投资和市场的超额收益的协方差除以超额市场收益与无风险利率的方差。
贝塔系数还可用于衡量资产相对于市场的波动程度。例如，假设某资产的贝塔值为1.5。该资产被认为比市场波动性高50%。
贝塔系数在比较不同资产时非常有用—，很容易识别出贝塔系数为1.5的投资比贝塔系数为1.3的投资波动性更大。
例如，假设基金A的比较基准为沪深300指数，经回归计算后得到基金A的$\beta$值为1.2。那么当沪深300指数上涨10%时，基金A预期将上涨12%；当沪深300指数下跌10%时，基金A相对应预期将下降12%。则表示基金的实际收益率超过它所承受风险对应的预期收益的部分。
同样以基金A举例，若沪深300指数上涨10%，而基金A实际上涨了15%，则基金A的$\alpha$即为超过预期收益的部分15%-1.2 * 10%=3%。
$\alpha$越大说明基金经理的管理水平越高。因由经济学家迈克尔·詹森提出，因此。$\alpha$有时也会叫做詹森指数。

卡玛比率

卡玛比率描述的是收益和最大回撤之间的关系，也可以叫做“单位回撤收益率”，其计算公式为：

$卡玛比率=区间年化收益率/区间最大回撤$

卡玛比率更加关注最大损失风险，是“固收+”基金的重要关注指标。
卡玛比率越高的基金，持有体验越好。

月胜率

相比于一天、一周的时间内基金胜率受到市场波动的影响较大，而一年的时间频率又太低，以月为周期来评价基金胜率或许较为合理。
月胜率，指的是基金在每个月跑赢比较基准的概率。
如果一只以沪深300指数为比较基准的股票基金，其在一年的12个月中，有8个月都跑赢了沪深300指数，则该基金的月胜率为8/12=66.7%。
市场上，基金的月胜率一般在45%-60%之间，由此可见基金经理想要战胜市场不是一件容易的事情。

上/下行捕获比

上行捕获比代表比较基准上涨时，基金相对基准上涨幅度的比率；
下行捕获比代表比较基准下跌时，基金相对基准下跌幅度的比率。其计算公式分别为：

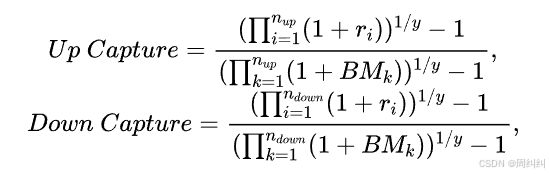
基准的月度收益率BM>0时，为上行环境，反之为下行环境。

举例说明$n_{up}$、$n_{down}$和$y$的含义：

• 如果一个基金运行了3年，那么一共有36个月，假设该基金的对应比较基准是沪深300指数
• 如果沪深300指数在这36个月中，有24个月是上涨的，那么$n_{up}$就为24，$n_{down}$就为12。“$1/y$”是为了让不同基金的上/下行捕获比具有可比性，起到将指标年化的作用。
• 这个例子中，计算上涨捕获比时，$y$等于上涨月份合计的年份，即2年；计算下行捕获比时，则$y$为1年。

夏普比率

夏普比率是衡量单位风险下的收益率情况，也就是每承担一单位风险所产生的风险补偿。风险和收益相当于硬币的两面，管理收益的本质是管理风险，在业绩评价中核心问题就是在承担现有的风险下，我们是否能获得足够的收益？

• 夏普提出的资本资产定价模型（CAPM）的核心逻辑就是在市场均衡的条件下，资产的收益率和承担的风险正相关，风险越大，收益率越高，夏普比率公式是

$SharpeRatio=\frac{R_P-R_f}{{\sigma }_P}$

式中，$S_R$为夏普比率，$R_P$ 表示投资组合收益率，$R_f$表示无风险收益率，可用一年期国债收益率代替,${\sigma }_P$表示投资组合风险（也就是收益率的标准差）

索提诺比率

与夏普比率类似，索提诺比率同样是衡量基金收益风险比的指标。不同的是，该指标认为向上的波动是有利的波动，只有向下的波动才是风险。具体计算公式如下：

$SortinoRatio=\frac{R_P-R_f}{D_R}$

其中，$R_P$为投资组合的年化收益率，$R_f$为年化无风险利率，$D_R$为下行标准差。下行标准差的计算公式是
$\text{下行标准差}=\sqrt{\frac{{\sum }_{i=1}^n(r_i-r_T{)}^2}{n}}$

其中，$r_i$为基金第$i$期的收益率，$r_T$为目标收益率，不一定为0，$n$表示基金收益率小于目标收益率的期数，只有$r_i$小于$r_T$时才将数据纳入计算。

• 通常情况下，需要对下行标准差进行年化处理，如果收益率采用每日收益，则乘以交易日数量的开方,一般是$\sqrt{252}$；
• 如果收益率采用每月收益，则乘以12的开方,$\sqrt{12}$。

最后回到索提诺比率，索提诺比率越大，说明基金的投资水平越高。
但和夏普比率相比，索提诺比率这一衡量标准更符合那些对资产价值下跌较为敏感的投资者。

经风险调整的收益率（2）

我们根据夏普比率可以将投资组合进行排序，但很难量化个组合之间业绩优劣的差异程度，因此，可以将投资组合的收益率根据基准组合的标准差进行修正，就得到经风险调整的收益率（2），统一将投资组合收益率根据基准组合的标准差进行修正，以基准组合的风险水平为基础，能够很好的比较不同风险的投资组合收益率，该收益率具有直接可比性，$M2$减去基准组合收益率就可以得到投资组合的超额收益率;

$M^2=R_p+SR\times ({\sigma }_p-{\sigma }_M)=(R_p-R_f)\times \frac{{\sigma }_M}{{\sigma }_p}+R_f$

式中，2表示经风险调整的收益率，$R_P$表示投资组合的收益率，SR 为夏普比率，${\sigma }_M$表示基准组合的标准差，${\sigma }_P$表示投资组合的标准差，$R_f$表示无风险收益率。

特雷诺比率

特雷诺比率是以基金收益的系统风险作为基金绩效调整的因子，反映基金承担单位系统风险所获得的超额收益。该指数计算公式为

$T=\frac{R_P-R_f}{{\beta }_P}$

其中$T$即特雷诺比率，$R_P$为基金收益率，$R_f$为无风险收益率，${\beta }_P$为基金的系统性风险。需要注意的是，${\beta }_P$为CAPM模型下回归计算得出的系数，与上述由单指数模型得出的有所不同。CAPM模型为：

$R_P=R_f+{\beta }_P(R_M-R_f)$
其中$R_P$为市场收益率。

特雷诺比率越大，表明基金的单位风险溢价越高，基金的绩效越好。

信息比率IR

收益率波动率、夏普比率、经风险调整的收益率（2）等都是绝对风险指标，而信息比率（IR）也称作修正夏普比率，经常被用于评价投资经理的能力，也是相对风险指标，绝对风险指标是将投资组合和参考基准的风险和收益分别计算，然后将两者进行比较，而相对风险指标则是

• 首先关注投资组合超越基准的超额收益率，
• 其次，关注超额收益率的标准差，
• 最后，测量信息比率指标，正的 IR 代表超额收益率，负的则表示投资组合低于基准收益率。

$\epsilon =\sqrt{\frac{{\sum }_{i=1}^n(a_i-\overline{a}{)}^2}{n}}$

$IR=\frac{a}{\epsilon }$

式中，
$\epsilon$表示跟踪误差,投资组合的收益率与基准组合的收益率之差的标准差,
$a_i$表示第 $i$ 期的超额收益率，
$\overline{a}$表示超额收益率的均值，
$IR$代表信息比率，
$a$代表超额收益率。

风险价值(VaR)

条件风险价值(CVaR)

$R^2$

R平方是一种统计指标，表示可以用基准指数的变动来解释的基金投资组合或资产变动的百分比。
R平方值的范围从0到1，通常以百分比形式表示（0%到100%）。
R平方值为0.9意味着90%的分析解释了数据内90%的变异。
R平方值较高的风险模型表明模型中使用的自变量更多地解释了因变量的变化。
当尝试确定投资价格变化的原因时，R平方最有用。
它是金融模型的副产品，它阐明了哪些变量决定了其他变量的结果。
求R-Squared的公式是将未解释的方差（残差平方和）除以总方差（总平方和）。然后，用1减去这个商。
通常建议共同基金投资者避免使用高R平方比率的主动管理型基金，这些基金通常被分析师批评为“秘密”指数基金。
在这些情况下，由于每个投资篮子的表现都非常相似，当我们可以从指数基金获得相同或接近的结果时，为专业管理支付更高的费用就没有什么意义。