非支配性排序遗传算法 III---NSGA-III-可用于（多目标模型融合/特征选择与降维/图像多目标优化处理）

 非支配性排序遗传算法 III（NSGA-III）是用于求解多目标优化问题的一种进化算法1。以下是对它的具体介绍1：

 具体完整算法请跳转：非支配性排序遗传算法 III---NSGA-III-可用于（多目标模型融合/特征选择与降维/图像多目标优化处理）

发展背景

NSGA-III 由 Kalyanmoy Deb 和 Harshit Jain 提出，是在 NSGA-II 的基础上进行改进和扩展，以更好地处理多目标优化问题，尤其是在处理高维目标空间时相比传统多目标算法表现更优。

主要特点

• 多目标优化：专门用于处理三种或更多目标函数的优化问题，可同时优化多个相互冲突的目标，找到一组在多个目标上都没有其他解能同时更优的非支配解集。
• 参考点策略：引入了参考点的概念，通过在目标空间中生成固定数量且均匀分布的参考点来引导种群的进化，帮助保持解的多样性，并确保最终解在所有目标上的均匀性。
• 非支配排序：采用非支配排序的方式来评估个体的优劣，个体根据其支配关系被分为不同的等级（前沿），与 NSGA-II 中的非支配排序类似。
• 精英保留：使用精英策略，通过合并父代和子代种群，确保优秀的个体能够在下一代中得到保留，有利于算法更快地收敛到 Pareto 前沿。
• 选择机制优化：选择过程中不仅考虑非支配等级，还引入了与参考点的距离，综合这两个因素来选择更优个体，使得算法能够更好地平衡解的收敛性和多样性。

工作机制

• 种群初始化：随机生成初始种群，每个个体有一组决策变量，并计算其目标函数值，得到个体在目标空间中的表现。
• 生成参考点：根据目标函数的数量，生成均匀分布的参考点，这些参考点在目标空间中为种群的进化提供方向指导。
• 非支配排序：对种群进行非支配排序，确定每个个体的等级（如 F1、F2 等），并构建支配关系，将种群中的个体划分成不同的 Pareto 层级。
• 个体关联：将每个个体与最近的参考点关联，计算个体与参考点之间的距离，以此衡量个体与参考点的接近程度，为选择操作提供依据。
• 选择与繁殖：根据非支配等级和与参考点的距离进行选择，挑选出适应度较高的个体作为父代。然后采用交叉和变异等遗传操作生成新个体（子代），增加种群的多样性和探索能力。
• 更新种群：合并父代和子代，重新进行非支配排序，并使用与参考点的距离来选择最终种群，确保种群中的个体既具有良好的非支配性，又能均匀地分布在参考点周围。
• 迭代：重复执行上述步骤，直到满足终止条件，如达到最大迭代次数、找到满意的 Pareto 前沿或满足收敛条件等。

应用领域

• 工程设计优化：在机械工程、电气工程等领域，用于优化设计参数，如在汽车发动机设计中，同时优化动力输出、燃油经济性和排放等多个目标。
• 资源管理：在资源分配、调度等问题中，帮助合理分配资源，如电力系统中的电力分配，同时考虑发电成本、传输损耗和供电可靠性等目标。
• 路径规划：在物流配送、机器人路径规划等场景中，寻找同时满足距离最短、时间最少、成本最低等多目标的最优路径。
• 环境监测和管理：在环境科学领域，用于优化环境监测方案、资源配置等，如同时考虑监测成本、监测精度和覆盖范围等目标。
• 财务和投资策略优化：在金融领域，帮助投资者制定投资组合策略，同时优化收益、风险、流动性等多个目标。

• NSGA-III 在多目标优化领域有诸多创新思路，这些思路有效解决了传统算法在高维目标空间中的不足，显著提升了算法性能：

• 基于参考点的选择机制：在高维目标空间中，传统的基于拥挤度距离的选择方式效果不佳。NSGA-III 创新性地引入参考点，这些参考点均匀分布在目标空间中。算法通过计算个体与参考点的距离，将个体与参考点关联起来。这使得算法在选择时，不仅能保证收敛性，还能有效维持种群多样性。例如在复杂的工程设计多目标优化中，能让算法在众多设计方案中，筛选出在多个目标上分布均匀且接近最优解的方案。
• 非支配排序的改进应用：NSGA-III 沿用了 NSGA-II 中的非支配排序方法，并进一步深化其在高维目标下的应用。通过将种群划分为不同的非支配层级，优先处理层级靠前（即非支配程度高）的个体，让算法聚焦于更优的解空间进行搜索。在多目标资源分配问题中，通过非支配排序能快速定位到资源利用效率高、分配公平性好等综合表现更优的分配方案集合，为后续优化提供优质基础。
• 精英保留策略的强化：NSGA-III 在每一代进化过程中，将父代种群和子代种群合并，然后基于非支配排序和参考点关联进行筛选，确保优秀个体能进入下一代。这种强化的精英保留策略，使算法在迭代过程中不断积累和优化优良解，避免因遗传操作导致的最优解丢失，加速算法收敛到 Pareto 前沿。比如在多目标生产调度优化中，算法能持续保留生产效率高、成本低等综合性能优良的调度方案，并在此基础上进一步探索更优解。
• 适应高维目标空间的设计：针对多目标优化中目标数量增加导致的维度灾难问题，NSGA-III 从多个方面进行针对性设计。如参考点的设置能适应高维空间，为搜索提供方向；选择机制和排序方式在高维下依然能有效区分个体优劣，引导算法在复杂的高维目标空间中高效搜索，找到均匀分布且逼近最优的解集 ，这在涉及多目标的环境评估、复杂系统性能优化等实际问题中具有重要意义。

用于多目标模型融合

• 面临的多目标问题
  • 提升综合性能：不同模型在不同指标上可能各有优势，如有的模型准确率高但召回率低，有的则相反，需要将多个模型融合，使融合后的模型在准确率、召回率、F1 值等多个评价指标上都能达到较好的平衡。
  • 降低模型复杂度：在融合多个模型时，要避免模型过于复杂导致计算成本过高和过拟合等问题，需要在提升性能的同时，控制模型的复杂度，如减少模型参数数量、降低计算量等。
  • 提高泛化能力：使融合后的模型在不同的数据集和实际应用场景中都能有稳定且良好的表现，防止在训练集上表现好但在测试集或新数据上效果不佳的情况。
• NSGA-III 的作用方式
  • 编码个体：将参与融合的各个模型的权重或组合方式进行编码，作为 NSGA-III 中的个体。例如，若有三个模型进行融合，可以用一个三维向量表示每个个体，向量中的每个元素代表对应模型的融合权重。
  • 构建目标函数：以准确率、召回率、F1 值等性能指标以及模型复杂度相关指标（如参数数量、计算时间等）和泛化能力相关指标（如交叉验证准确率的稳定性等）作为多目标函数。通过调整模型融合权重，优化这些目标函数，寻找使多个目标都能达到较好平衡的模型融合方案。
  • 遗传操作与优化：NSGA-III 通过选择、交叉、变异等遗传操作，在模型融合权重的解空间中进行搜索。根据每个个体在多目标函数下的非支配排序和拥挤度等信息，选择优秀的个体进行遗传操作，不断更新种群，逐渐找到最优的模型融合权重组合，使融合后的模型在多个目标上实现优化。

用于特征选择与降维

• 面临的多目标问题
  • 信息保留：选择的特征子集要尽可能保留原始数据的关键信息，使基于这些特征训练的模型能够准确地描述数据的内在规律，不丢失重要的分类或预测信息。
  • 相关性与冗余性：要选择与目标变量相关性高且相互之间冗余度低的特征子集。高相关性有助于提高模型性能，低冗余度可以避免特征之间的重复信息对模型造成干扰，同时降低计算成本。
  • 计算效率：在大数据场景下，特征数量可能非常庞大，需要在保证特征质量的前提下，选择尽可能少的特征，以提高后续模型训练和预测的计算效率，减少存储和计算资源的消耗。
• NSGA-III 的作用方式
  • 个体表示：将特征选择问题编码为 NSGA-III 中的个体，通常可以用二进制向量表示，向量中的每个元素对应一个特征，取值为 0 或 1，表示该特征是否被选择。
  • 目标函数设计：构建以信息增益、与目标变量的相关性系数、特征之间的冗余度指标以及特征数量为目标的多目标函数。通过优化这些目标函数，找到既能保留足够信息、又具有低冗余度和较少数量的特征子集。
  • 搜索最优特征子集：NSGA-III 利用遗传算法的搜索机制，在特征子集的解空间中进行遍历搜索。通过不断地迭代更新种群，根据个体的非支配排序和拥挤度等信息，引导搜索方向，逐步找到在多个目标上都能达到较优平衡的最优特征子集，实现特征选择与降维的目的。

用于图像多目标优化处理

• 面临的多目标问题
  • 图像质量提升：需要同时提高图像的清晰度、对比度、色彩还原度等多个方面的质量指标，使处理后的图像在视觉效果上更加清晰、自然、真实。
  • 噪声抑制：在增强图像的同时，要有效地抑制各种噪声，如高斯噪声、椒盐噪声等，避免噪声对图像细节和特征的干扰，保证图像的质量和后续处理的准确性。
  • 细节保留：在进行图像去噪、增强等处理时，要尽可能保留图像的细节信息，如边缘、纹理等，防止在处理过程中丢失重要的图像特征，影响图像的视觉效果和后续的分析、识别等任务。
• NSGA-III 的作用方式
  • 参数编码：将图像优化算法中的参数，如滤波参数、对比度调整参数、色彩校正参数等进行编码，作为 NSGA-III 中的个体。例如，对于一个基于小波变换的图像去噪算法，可以将小波基函数的参数、阈值等作为个体的编码元素。
  • 多目标构建：以图像的清晰度评价指标（如梯度幅值、拉普拉斯算子响应等）、噪声抑制指标（如均方误差、峰值信噪比等）和细节保留指标（如结构相似性指数等）作为多目标函数。通过调整图像优化算法的参数，优化这些目标函数，寻找能够同时提升图像质量、抑制噪声和保留细节的最优参数组合。
  • 优化搜索过程：NSGA-III 在图像优化参数的解空间中进行搜索，通过遗传操作不断更新种群。根据每个个体在多目标函数下的非支配排序和拥挤度等情况，选择优秀的个体进行遗传操作，逐渐调整参数，找到使图像在多个质量指标上都能达到最佳平衡的最优参数，实现图像的多目标优化处理。

具体算法及实验结果

% 清除命令窗口内容
clc;
% 清除工作区变量
clear;
% 关闭所有打开的图形窗口
close all;

%% Problem Definition
% 定义目标函数句柄，这里使用 MOP2 函数作为目标函数
CostFunction = @(x) MOP2(x);  

% 决策变量的数量
nVar = 5;    

% 决策变量矩阵的大小
VarSize = [1 nVar]; 

% 决策变量的下限
VarMin = -1;   
% 决策变量的上限
VarMax = 1;   

% 目标函数的数量，通过随机生成一组变量计算目标函数值来确定
nObj = numel(CostFunction(unifrnd(VarMin, VarMax, VarSize)));

%% NSGA-II Parameters
% 生成参考点
% 划分的数量，用于确定参考点的分布
nDivision = 10; 
% 调用 GenerateReferencePoints 函数生成参考点
Zr = GenerateReferencePoints(nObj, nDivision); 

% 最大迭代次数
MaxIt = 50;  

% 种群大小
nPop = 80;  

% 交叉概率
pCrossover = 0.5;       
% 交叉操作产生的后代数量
nCrossover = 2*round(pCrossover*nPop/2); 

% 变异概率
pMutation = 0.5;       
% 变异操作产生的个体数量
nMutation = round(pMutation*nPop);  

% 变异率
mu = 0.02;     

% 变异步长
sigma = 0.1*(VarMax-VarMin); 

%% Collect Parameters
% 将种群大小存储到结构体 params 中
params.nPop = nPop;
% 将参考点存储到结构体 params 中
params.Zr = Zr;
% 参考点的数量
params.nZr = size(Zr,2);
% 目标函数的最小值，初始为空
params.zmin = [];
% 目标函数的最大值，初始为空
params.zmax = [];
% 其他最小值相关参数，初始为空
params.smin = [];

%% Initialization
% 显示开始运行 NSGA-III 的提示信息
disp('Starting NSGA-III ...');

% 创建一个空个体结构体，用于存储个体信息
empty_individual.Position = [];
empty_individual.Cost = [];
empty_individual.Rank = [];
empty_individual.DominationSet = [];
empty_individual.DominatedCount = [];
empty_individual.NormalizedCost = [];
empty_individual.AssociatedRef = [];
empty_individual.DistanceToAssociatedRef = [];

% 初始化种群，每个个体都为上述的空个体结构体
pop = repmat(empty_individual, nPop, 1);
% 初始化每个个体的位置和目标函数值
for i = 1:nPop
    pop(i).Position = unifrnd(VarMin, VarMax, VarSize);
    pop(i).Cost = CostFunction(pop(i).Position);
end

% 对种群进行排序并选择，更新种群、前沿集合和参数
[pop, F, params] = SortAndSelectPopulation(pop, params);

%% NSGA-II Main Loop
% 主循环，进行迭代优化
for it = 1:MaxIt
    % 交叉操作
    popc = repmat(empty_individual, nCrossover/2, 2);
    for k = 1:nCrossover/2
        % 随机选择两个父代个体
        i1 = randi([1 nPop]);
        p1 = pop(i1);
        i2 = randi([1 nPop]);
        p2 = pop(i2);
        % 进行交叉操作，生成两个子代个体的位置
        [popc(k, 1).Position, popc(k, 2).Position] = Crossover(p1.Position, p2.Position);
        % 计算子代个体的目标函数值
        popc(k, 1).Cost = CostFunction(popc(k, 1).Position);
        popc(k, 2).Cost = CostFunction(popc(k, 2).Position);
    end
    % 将子代个体矩阵转换为向量形式
    popc = popc(:);

    % 变异操作
    popm = repmat(empty_individual, nMutation, 1);
    for k = 1:nMutation
        % 随机选择一个父代个体
        i = randi([1 nPop]);
        p = pop(i);
        % 对父代个体进行变异操作，生成变异后的个体位置
        popm(k).Position = Mutate(p.Position, mu, sigma);
        % 计算变异后个体的目标函数值
        popm(k).Cost = CostFunction(popm(k).Position);
    end

    % 合并父代、子代和变异后的个体
    pop = [pop
           popc
           popm]; %#ok
    
    % 对合并后的种群进行排序并选择，更新种群、前沿集合和参数
    [pop, F, params] = SortAndSelectPopulation(pop, params);
    
    % 提取第一前沿的个体
    F1 = pop(F{1});

    % 显示当前迭代信息，包括迭代次数和第一前沿个体的数量
    disp(['Iteration ' num2str(it) ': Number of F1 Members = ' num2str(numel(F1))]);

    % 绘制第一前沿个体的目标函数值
    figure(1);
    PlotCosts(F1);
    pause(0.01);
end

%% Results
% 显示最终迭代的第一前沿个体数量
disp(['Final Iteration: Number of F1 Members = ' num2str(numel(F1))]);
% 显示优化结束的提示信息
disp('Optimization Terminated.');

实验结果分析

• 第一前沿个体数量：通过每次迭代显示的第一前沿个体数量，可以观察到算法在迭代过程中第一前沿个体数量的变化情况。若数量逐渐稳定，表明算法可能已收敛；若数量持续波动，可能表示算法还在探索解空间。
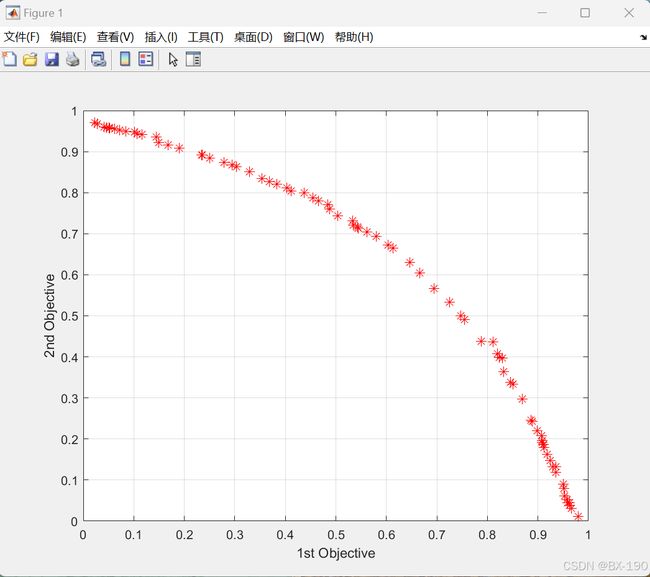
• 目标函数值的可视化：通过PlotCosts(F1)函数绘制第一前沿个体的目标函数值，可以直观地观察到算法找到的 Pareto 前沿的形状和分布情况。一个好的 Pareto 前沿应该是均匀分布且尽可能接近真实的 Pareto 前沿。
• 收敛性：结合迭代次数和第一前沿个体的目标函数值变化，可以判断算法是否收敛。如果在多次迭代后，第一前沿个体的目标函数值不再有明显改善，说明算法已经收敛。
• 多样性：从绘制的 Pareto 前沿可以看出解的多样性。若解在目标空间中分布均匀，说明算法能够保持较好的多样性；若解集中在某些区域，可能需要调整算法参数以提高多样性。

具体完整算法请跳转：非支配性排序遗传算法 III---NSGA-III-可用于（多目标模型融合/特征选择与降维/图像多目标优化处理）