嵌入式学习笔记-卡尔曼滤波,PID,MicroPython
文章目录
-
- 卡尔曼滤波
-
- 卡尔曼滤波的核心思想
- 卡尔曼滤波的数学模型
-
- 1. 状态转移模型(预测系统状态)
- 2. 观测模型(预测测量值)
- 卡尔曼滤波的五个关键步骤
-
- 1. 预测状态
- 2. 预测误差协方差
- 3. 计算卡尔曼增益
- 4. 更新状态
- 5. 更新误差协方差
- 卡尔曼滤波算法步骤总结
- 代码实现(Python 示例)
- PID调节
-
- 总结
- MicroPython
-
- 示例代码:控制 LED 灯并连接 WiFi
-
- 1. 硬件准备
- 2. 连接方式
- 3. 示例代码
- 代码说明
- 开发环境搭建
今天开组会,中午没睡困得要死,但是每天都得不停学习。
参考下面视频
卡尔曼滤波
卡尔曼滤波是一种用于估计动态系统状态的算法,它是一种线性递归滤波
器,即使测量数据中存在噪声,它也能提供对真实状态的最佳估计。这种滤波算法在控制系统、导航、信号处理等领域应用广泛。
卡尔曼滤波的核心思想
卡尔曼滤波是一种递归估计算法,它在每个时刻执行两步:
- 预测阶段:根据上一时刻的状态,利用系统的动态模型预测当前时刻的状态。
- 更新阶段:结合当前的测量数据,校正预测值,得到更准确的状态估计。
卡尔曼滤波的数学模型
卡尔曼滤波假设系统可以用线性模型描述,并且噪声服从高斯分布。系统模型由以下两部分组成:
1. 状态转移模型(预测系统状态)
x k = F k x k − 1 + B k u k + w k x_k = F_k x_{k-1} + B_k u_k + w_k xk=Fkxk−1+Bkuk+wk
- x k x_k xk:系统在时刻 k k k 的状态向量(例如位置、速度)。
- F k F_k Fk:状态转移矩阵,描述状态之间的变化关系。
- B k B_k Bk:控制输入矩阵,描述控制输入对状态的影响。
- u k u_k uk:控制输入。
- w k w_k wk:过程噪声,服从均值为 0 0 0,协方差为 Q Q Q 的高斯分布。
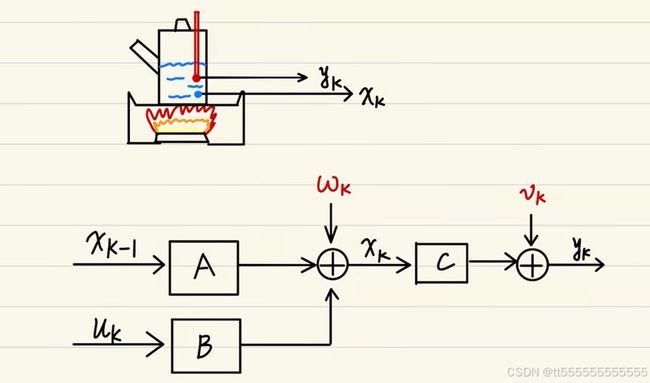
2. 观测模型(预测测量值)
z k = H k x k + v k z_k = H_k x_k + v_k zk=Hkxk+vk
- z k z_k zk:时刻 k k k 的观测值。
- H k H_k Hk:观测矩阵,描述状态如何映射到观测空间。
- v k v_k vk:测量噪声,服从均值为 0 0 0,协方差为 R R R 的高斯分布。
卡尔曼滤波的五个关键步骤
1. 预测状态
根据状态转移模型,预测当前时刻的状态:
x ^ k − = F k x ^ k − 1 + B k u k \hat{x}_k^- = F_k \hat{x}_{k-1} + B_k u_k x^k−=Fkx^k−1+Bkuk
这里, x ^ k − \hat{x}_k^- x^k− 表示预测的状态。
2. 预测误差协方差
预测状态的误差协方差:
P k − = F k P k − 1 F k T + Q P_k^- = F_k P_{k-1} F_k^T + Q Pk−=FkPk−1FkT+Q
- P k − P_k^- Pk−:预测误差协方差矩阵,反映预测值的不确定性。
- Q Q Q:过程噪声协方差矩阵。
3. 计算卡尔曼增益
根据预测的不确定性和测量的不确定性计算卡尔曼增益:
K k = P k − H k T ( H k P k − H k T + R ) − 1 K_k = P_k^- H_k^T (H_k P_k^- H_k^T + R)^{-1} Kk=Pk−HkT(HkPk−HkT+R)−1
- K k K_k Kk:卡尔曼增益,决定了预测和测量数据的权重。
4. 更新状态
结合测量值更新状态估计:
x ^ k = x ^ k − + K k ( z k − H k x ^ k − ) \hat{x}_k = \hat{x}_k^- + K_k (z_k - H_k \hat{x}_k^-) x^k=x^k−+Kk(zk−Hkx^k−)
- z k − H k x ^ k − z_k - H_k \hat{x}_k^- zk−Hkx^k−:测量残差(即预测值与观测值的差异)。
5. 更新误差协方差
更新误差协方差矩阵:
P k = ( I − K k H k ) P k − P_k = (I - K_k H_k) P_k^- Pk=(I−KkHk)Pk−
- I I I:单位矩阵。
卡尔曼滤波算法步骤总结
- 初始化:设定初始状态 x ^ 0 \hat{x}_0 x^0 和初始协方差矩阵 P 0 P_0 P0。
- 循环执行:
- 预测状态 x ^ k − \hat{x}_k^- x^k− 和协方差 P k − P_k^- Pk−。
- 计算卡尔曼增益 K k K_k Kk。
- 更新状态 x ^ k \hat{x}_k x^k 和协方差 P k P_k Pk。
代码实现(Python 示例)
以位置和速度为状态(经典一维运动模型)为例:
import numpy as np
# 初始化参数
F = np.array([[1, 1], [0, 1]]) # 状态转移矩阵
H = np.array([[1, 0]]) # 观测矩阵
Q = np.array([[1, 0], [0, 1]]) # 过程噪声协方差
R = np.array([[10]]) # 测量噪声协方差
B = np.array([[0], [0]]) # 控制输入矩阵
u = np.array([[0]]) # 控制输入
# 初始状态和协方差
x = np.array([[0], [1]]) # 初始状态:[位置, 速度]
P = np.array([[1, 0], [0, 1]]) # 初始误差协方差
# 模拟观测数据
z_real = [5, 6, 7, 9, 10] # 实际观测值
for z in z_real:
# 预测阶段
x_predict = F @ x + B @ u
P_predict = F @ P @ F.T + Q
# 计算卡尔曼增益
K = P_predict @ H.T @ np.linalg.inv(H @ P_predict @ H.T + R)
# 更新阶段
z = np.array([[z]]) # 当前观测值
x = x_predict + K @ (z - H @ x_predict)
P = (np.eye(2) - K @ H) @ P_predict
# 输出当前状态估计
print("位置估计:", x[0, 0], "速度估计:", x[1, 0])
PID调节
之前学过点,所以就简单学下怎么调节。
| 环节 | 功能描述 | 作用 | 优点 | 缺点 | 实际应用注意事项 |
|---|---|---|---|---|---|
| P(比例环节) | 将比例系数与偏差信号e(t)相乘后输出 | 快速响应系统误差,调节系统向误差减小的方向移动 | 响应迅速,能快速调整系统 | 可能引起系统震荡,存在稳态误差 | 1. 比例增益系数KP不能过大,以避免震荡。 通过逐步增大KP,找到系统等幅振荡时的KP值,取其70%作为最优比例增益系数。 |
| I(积分环节) | 对偏差信号e(t)进行积分,使输出持续增加或减少,直至偏差为零 | 消除稳态误差 | 消除稳态误差,提高系统精度 | 可能引起系统惯性干扰,导致响应变慢 | 1. 在无过谐振荡、稳态误差近似为0时,积分时间常数TI取值合理。 与比例环节结合(PI控制),可同时提高响应速度和消除稳态误差。 |
| D(微分环节) | 对偏差信号e(t)的变化率进行反馈,提前修正偏差 | 减少调节时间,提前校正系统 | 提高动态性能,减少超调 | 对噪声敏感,可能导致误调节 | 1. 在动态系统中,微分环节可以提前发出校正信号,防止偏差扩大。 |
总结
- P环节:快速响应,但可能导致震荡和稳态误差。
- I环节:消除稳态误差,但可能使系统响应变慢。
- D环节:提前校正偏差,提高动态性能,但对噪声敏感。
三者结合(PID控制)可综合各环节的优点,克服单一环节的缺点,广泛应用于闭环控制系统中,以实现快速、稳定且无误差的控制效果。感觉PID可以对应快准稳。P越大,冲的越快,I适度,可以用来调节冲刺到最后的精度,D适度可以用来调价波痕,更加稳定。
MicroPython
MicroPython 是一种轻量级的 Python 解释器,专为嵌入式系统和微控制器设计,能够在资源受限的硬件上运行。它保留了 Python 的核心语法,同时提供了丰富的硬件控制接口,非常适合在 ESP32 等单片机上开发。
以下是一个基于 ESP32 单片机的 MicroPython 示例代码,介绍如何通过 GPIO 控制 LED 灯的闪烁,并连接 WiFi 网络。
示例代码:控制 LED 灯并连接 WiFi
1. 硬件准备
- ESP32 开发板
- 一个 LED 灯
- 电阻(可选)
- 杜邦线若干
2. 连接方式
将 LED 的正极连接到 ESP32 的 GPIO 引脚(如 GPIO 5),负极通过电阻连接到 GND。
3. 示例代码
以下代码展示了如何控制 GPIO 引脚来点亮和熄灭 LED,并连接到 WiFi 网络。
# 导入必要的模块
from machine import Pin
import network
import time
# 初始化 LED 引脚
led = Pin(5, Pin.OUT) # GPIO 5 作为输出
# 定义 WiFi 连接函数
def connect_wifi(ssid, password):
wlan = network.WLAN(network.STA_IF) # 创建 WLAN 对象
wlan.active(True) # 激活 WiFi 接口
if not wlan.isconnected(): # 检查是否已连接
print("Connecting to WiFi...")
wlan.connect(ssid, password) # 连接到指定 WiFi
while not wlan.isconnected(): # 等待连接
pass
print("Connected to WiFi!")
print("IP Address:", wlan.ifconfig()[0]) # 打印 IP 地址
# 连接到 WiFi
connect_wifi("your_ssid", "your_password") # 替换为你的 WiFi 名称和密码
# 主循环:控制 LED 闪烁
while True:
led.value(1) # 点亮 LED
time.sleep(1) # 等待 1 秒
led.value(0) # 熄灭 LED
time.sleep(1) # 等待 1 秒
代码说明
-
GPIO 控制:
- 使用
machine.Pin模块控制 GPIO 引脚。 Pin(5, Pin.OUT)表示将 GPIO 5 设置为输出模式。led.value(1)和led.value(0)分别用于点亮和熄灭 LED。
- 使用
-
WiFi 连接:
- 使用
network模块连接到 WiFi 网络。 network.WLAN(network.STA_IF)创建一个 WiFi 客户端对象。wlan.connect(ssid, password)用于连接到指定的 WiFi 网络。
- 使用
开发环境搭建
-
固件烧录:
- 从 MicroPython 官网下载适用于 ESP32 的固件。
- 使用
esptool.py工具将固件烧录到 ESP32 开发板。
-
IDE 选择:
- 推荐使用 Thonny IDE 或 uPyCraft IDE。
- 在 Thonny 中配置 MicroPython 解释器,并连接到 ESP32 的串口。