递推9~15
题单地址:题单中心-东方博宜OJ
1298. 摘花生问题
问题描述
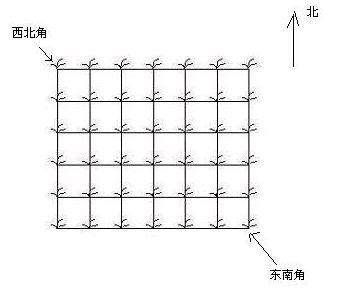
Hello Kitty 想摘点花生送给她喜欢的米老鼠。她来到一片有网格状道路的矩形花生地(如下图),从西北角进去,东南角出来。地里每个道路的交叉点上都有种着一株花生苗,上面有若干颗花生,经过一株花生苗就能摘走该它上面所有的花生。Hello Kitty 只能向东或向南走,不能向西或向北走。问 Hello Kitty 最多能够摘到多少颗花生。
如输入:
2 2
1 1
3 4
代表有 2 行,每行有 2 株花生,那么摘能摘到的最多的花生就是:1 -> 3 -> 4 ,总和为 8 颗花生。
输入
第一行是两个整数 n 和 m ( 1 ≤ n, m ≤ 100 ),代表了花生地里有 n 行,每行有 m 列的花生!
后面 n 行,每行有 m 个整数代表了每行中,每株花生的数量!( 每株花生数量 ≤ 10000 )
输出
输出是一个整数,代表了最多能摘到的花生的总数;
样例
输入
2 2
1 1
3 4
输出
8
解析:每一格的花生数量来源于其左方的数量和上方的数量,那么在两个方向中选择数量最多的,依次枚举每一格的最大花生数量,得到递推式:f(i, j) = max(f(i-1, j), f(i, j-1)),答案就在f(n, m)。
#include
using namespace std;
long long a[105][105];
int main() {
int m, n;
cin >> n >> m;
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
cin >> a[i][j];
}
}
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
a[i][j] += max(a[i-1][j], a[i][j-1]);
}
}
cout << a[n][m];
return 0;
} 1374. 摘花生问题(2)
问题描述
Hello Kitty 又一次来到花生地里摘花生,从左上角进入花生地,从右下角出去,只能向右或者向下,请问 Hello Kitty 应该沿着什么样的路线走,能够摘到的花生数量最多(假设花生地里没有任何 2 株的花生一样多,也不存在多条路线能够摘到一样多的花生的情况)?
比如输入:
2 2
1 2
3 4
应该输出:1−3−4,也就是按照 1 3 4 这三株数量的花生摘过去,能够摘到最多的花生!
输入
第一行是 2 个整数 m 和 n (2 ≤ m, n ≤ 100),代表花生地有 m 行,n 列花生!
后面 m 行,每行有 n 个整数代表了每行中,每株花生的数量。
输出
输出Hello Kitty按照走过的路线中,摘到每株花生的数量。
样例
输入
2 2
1 2
3 4
输出
1-3-4
解析:求最大值上道题已经讲过,输出路径使用递归来输出,从(n, m)点开始往后递归,每次找两个方向的最大值递归,直到(1, 1)。
#include
using namespace std;
long long a[105][105];
void dfs(int x, int y) {
if(x == 1 && y == 1){
cout << a[1][1];
return;
}
if(a[x][y-1] > a[x-1][y]){
dfs(x, y-1);
cout << "-" << a[x][y] - a[x][y-1];
}
else{
dfs(x-1, y);
cout << "-" << a[x][y] - a[x-1][y];
}
}
int main() {
int m, n;
cin >> n >> m;
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
cin >> a[i][j];
}
}
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
a[i][j] += max(a[i-1][j], a[i][j-1]);
}
}
dfs(n, m);
return 0;
} 1368. 蜜蜂路线
问题描述
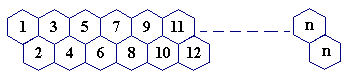
一只蜜蜂在下图所示的数字蜂房上爬动,已知它只能从标号小的蜂房爬到标号大的相邻蜂房,现在问你:蜜蜂从蜂房 M 开始爬到蜂房NN,1 ≤ M < N ≤100,有多少种爬行路线?
输入
输入 M,N 的值。(1 ≤ M < N ≤ 100)
输出
爬行有多少种路线。
样例
输入
1 14
输出
377
输入
1 100
输出
354224848179261915075
解析:到达 i 巢穴有两条路径,分别可以从 i-1 和 i-2 的巢穴到达,那么就和上一道题相似,i巢穴的方案数等于 i-1 巢穴加上 i-2 巢穴的方案数。需要注意的是结果可能会超过 long long 存储的范围,需要使用高精度来存储计算过程。
#include
using namespace std;
int a[1005][1005], k = 1;
void add(int x){
for(int i = 0; i < k; i++){
a[x][i] = a[x-1][i] + a[x-2][i];
}
for(int i = 0; i < k; i++){
if(a[x][i] > 9){
a[x][i+1] += a[x][i] / 10;
a[x][i] %= 10;;
}
}
if(a[x][k])k++;
}
int main() {
int m, n;
cin >> m >> n;
a[m][0] = 1;
for(int i = m+1; i <= n; i++){
add(i);
}
for(int i = k-1; i >= 0; i--){
cout << a[n][i];
}
return 0;
} 1367. 骨牌铺方格
问题描述
有 1×n(n ≤ 50)的一个长方形,用 1×1、1×2 和 1×3 的骨牌铺满方格,请问有多少种铺法?
例如当 n=3 时为 1×3 的方格。此时用 1×1 、1×2 和 1×3 的骨牌铺满方格,共有四种铺法。如下图:
输入
一个整数 n(n ≤ 50)
输出
骨牌的铺法。
样例
输入
3
输出
4
解析:一共有三种骨牌分别可以填满1、2、3格,假设要填满到第 i 格方格,在第 i-1格方块我们只需方一个1个的骨牌就可填满,其他两种骨牌以此类推,分别在 i-2 格和 i-3 格方块放一个就课填满,那么第 i 格的方案数等于前三格的方案数之和。n = 1 时方案数永远为1,前三格都需要在方案数的基础上加1,因为可以放一个骨牌就可以填满。
#include
using namespace std;
int a[55] = {0, 1, 2, 4};
int main() {
int n;
cin >> n;
for(int i = 4; i <= n; i++){
a[i] = a[i-1] + a[i-2] + a[i-3];
}
cout << a[n];
return 0;
} 1539. 小X放骨牌
问题描述
小X喜欢下棋。
这天,小X对着一个长为N宽为M 的矩形棋盘发呆,突然想到棋盘上不仅可以放棋子, 还可以放多米诺骨牌。
每个骨牌都是一个长为2宽为1的矩形,当然可以任意旋转。小X想知道在骨牌两两不重叠的前提下,这个棋盘上最多能放多少个骨牌,希望你帮帮他。
如图所示,三种颜色分别对应了三个骨牌。
输入
第一行包含用一个空格隔开的两个整数N, M。
输出
第一行包含一个整数,表示该棋盘上最多能放的骨牌个数。
样例
输入
2 3
输出
3
解析:骨牌的放置数量只与棋盘的总面积有关,所以总面积除以骨牌的面积2。
#include
using namespace std;
int main() {
int n, m, sum = 0;
cin >> n >> m;
sum = n * m / 2;
cout << sum;
return 0;
} 1366. 平面分割问题
问题描述
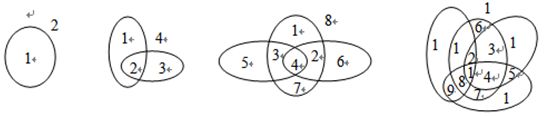
设有 n 条封闭曲线画在平面上,而任何两条封闭曲线恰好相交于两点,且任何三条封闭曲线不相交于同一点,问这些封闭曲线把平面分割成的区域个数。
输入
一个整数n(n <= 10000),代表封闭曲线的条数
输出
n条曲线分割区域的个数
样例
输入
2
输出
4
解析:当 n = 1 时,一条封闭曲线将平面分割成2个区域,即 f(1) = 2。当已经有 n - 1 条封闭曲线时,平面被分割成了 f(n - 1) 个区域。现在再增加第n条封闭曲线,由于任何两条封闭曲线恰好相交于两点,所以第n条封闭曲线与前面的 n - 1 条封闭曲线都相交,且有 2(n - 1) 个交点。这 2(n - 1) 个交点将第n条封闭曲线分成了 2(n - 1) 段弧。每一段弧都会把原来所在的区域一分为二,也就是每增加一段弧就会增加一个区域,所以增加第n条封闭曲线后,增加的区域个数为 2(n - 1)。因此,可以得到递推公式:f(n) = f(n - 1) + 2(n - 1)。
#include
using namespace std;
int a[10005] = {0, 2};
int main(){
int n;
cin >> n;
for(int i = 2; i <= n; i++){
a[i] = a[i-1] + 2 * (i - 1);
}
cout << a[n];
return 0;
} 1369. Pell数列
问题描述
有一种数列,它的前 10 项的值分别为:1 2 5 12 29 70 169 408 985 2378,这个数列被称为 Pell 数列,请问该数列的第 n 项的值是多少?(n ≤ 1000)
输入
一个整数 n 。
输出
第 n 项的值。
样例
输入
10
输出
2378
解析:分析前10项的值,可以总结出递推式:f(i) = f(i-1) * 2 + f(i-2) 。注意 n 的取值范围,计算是的数据会超过 long long 的存储范围,需要使用高精度计算存储。
#include
using namespace std;
int a[1005][1005], k = 1;
void add(int d){
for(int i = 0; i < k; i++){
a[d][i] = a[d-1][i] * 2 + a[d-2][i];
}
for(int i = 0; i < k; i++){
if(a[d][i] > 9){
a[d][i+1] += a[d][i] / 10;
a[d][i] %= 10;
}
}
if(a[d][k])k++;
}
int main(){
int n;
cin >> n;
a[1][0] = 1;
a[2][0] = 2;
for(int i = 3; i <= n; i++){
add(i);
}
for(int i = k-1; i >= 0; i--){
cout << a[n][i];
}
return 0;
}