MFCC

在语音识别研究领域，音频特征的选择至关重要。在这里介绍一种非常成功的音频特征——Mel Frequency Cepstrum Coefficient(MFCC),中文名字为梅尔频率倒谱系数。MFCC特征的成功很大程度上得益于心理声学的研究成果，它对人的听觉机理进行了建模。我们知道音频信号从时域信号转化为频域信号之后，我们可以得到各种频率分量的能量分布。心理声学的研究结果表明，人耳对于低频信号更加敏感，对于高频信号less sensitive，具体是一种什么关系？心理声学研究结果表明，在低频部分是一种线性的关系，但是随着频率的升高，人耳对于频率的敏感程度呈现对数增长的态势。这意味着仅仅从各个频率能量的分布设计符合人的听觉习惯的音频特征不是非常合理的。

　　MFCC 特征的设计者正式利用了上述人类的听觉特性，使用了梅尔滤波器来对频率分布进行滤波。这里的梅尔滤波器的设计充分体现了上面提到的人的听觉机理的问题。下面我们将详细介绍MFCC特征。

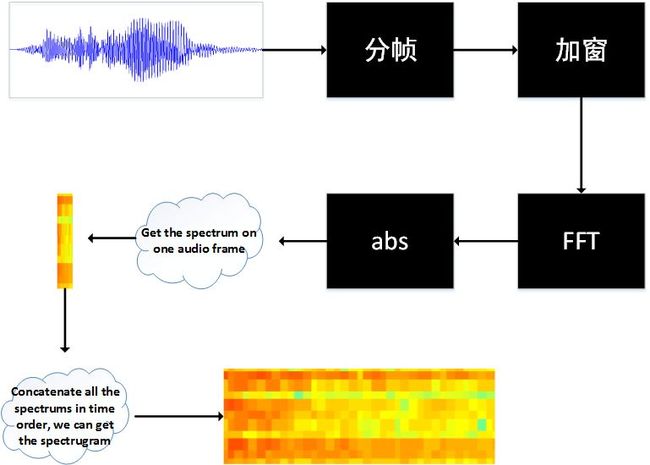
一、作为一种频率域的音频特征，离散傅里叶变换是这些特征计算的基础。一般我们会选择快速傅里叶变换FFT算法。

     相关的能量的求取解释可以参考FFT部分，一个比较粗略的流程是这样的。

二、梅尔滤波器

实际上是一种三角形滤波器，首先对frequency通过下面的公式映射到mel 标度

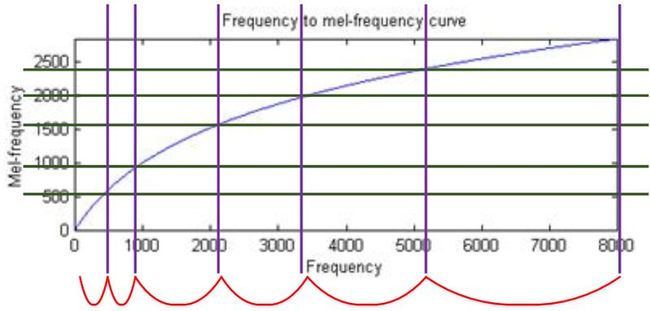
下面这张图充分体现了两者的关系。

在mel scale我们是对其进行等宽度的划分，但是在frequency scale可以看到，随之而变化的幅度确实逐渐变大的，在低频部分刚开始并不是非常明显的，但是随着频率的增大，这种趋势变得愈加明显。

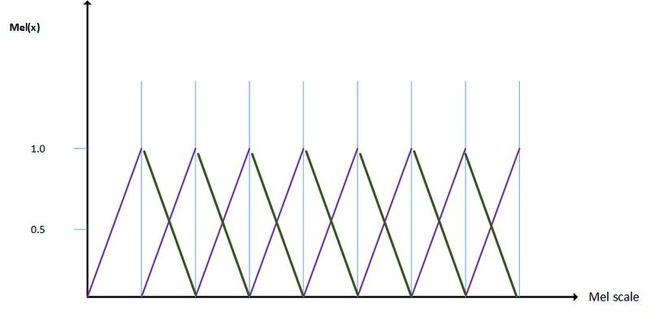
mel三角形滤波器的设计是在mel scale进行的，相邻滤波器之间存在交叉的部分，下一个滤波器的开始位置是上一个滤波器的中心频率位置，假设mel scale的范围为[0,max],假设要划分为N个梅尔滤波器，根据上面的分析，我们要将其等距划分为N+1块，如下所示。我们要获得7个mel filter，则将mel scale等间距划分为了8个区域，使用如图所示的方式可以得到7个filter。每个三角形的中间位置是mel滤波器的中间位置，将其使用上面的公式的反变换，反变换到frequency，可以得到相应的mel滤波器的中心频率。

当然上面这张图的目的只是为了确定mel滤波器的边界，在实际当中的mel滤波器的filter过程是使用了在相对应的频率域的公式来进行的

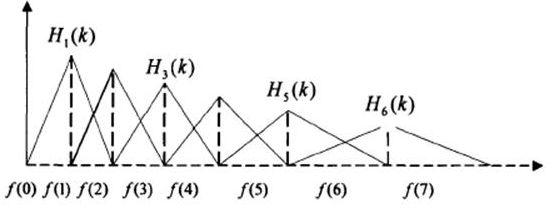
如下所示，我们可以得到在频率域的mel滤波器。通过上面的计算我们可以得到相应的N+1个三角滤波器的frequency的边界，我们将其记为$f(m),m=0,1,2,...,N$

下面的有的图像引用自http://my.oschina.net/jamesju/blog/193343，在此版权说明

我们会发现上面的公式的分母是一个常数，而且随着frequency的增大，这个常数相对的也增大了，而且增大的幅度更大，所以造成整体的$H_{m}(k)变小$，从而说明随着频率的增大，相应的filter权重会变小，这也说明了对于低频部分的重视。

下面所示为滤波器的一个简单示意图。

上面的滤波的结果，是导致得到了N个值，因为每一个滤波器，会在对相应的频率能量加权之后，进行了求和运算。

三、非线性变换

一般为log对数运算

四、离散余弦变换  (DCT)

 

参考资料：

 

http://my.oschina.net/jamesju/blog/193343