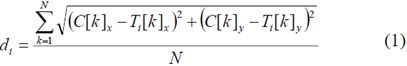两篇论文笔记

很久没写博客了，最近写了很多代码，虽然是对编程能力的一大锻炼，但是并没有什么感悟可以写成合集，所以也就不提了，C++学习之路任重道远。

勉勉强强完成了看100篇论文的任务，但泛读居多，真的很泛很泛。现在挑出被我实现的两篇来说一下，基于模板的手势识别算法，很简单也挺直观的。

Gestures without Libraries, Toolkits or Training -- A $1 Recognizer for User Interface Prototypes

已知用户的手势是由一组候选点C组成的，我们必须确定现有的模板点集合T_i中哪一个最匹配。由于输入的数据包含很多噪点，且数据分布不均匀，因此需要重采样。

步骤1.重采样点的路径

首先，将原有的M个点来定义的路径定义成N个等距的点。在实践中，发现N=64是个不错的选择。

要进行重采样，首先要计算M个点的路径的总体长度，然后用这个长度除以(N-1)得到每个增量的长度I。然后沿着路径迭代添加新的点。最后，形成了C[k]到T[k]的映射(k=1,…,n)。

步骤2.基于”Indicative Angle”的旋转

一般来说，从0°开始蛮力地+1°旋转匹配手势直到360°，对于$1来说都不慢的。但是$1有更好的方法。定义手势的第一个点与手势的中心点之间形成的角为Indicative Angle。使用旋转函数来对其进行处理。

步骤3.缩放和平移

旋转之后，手势被缩放到引用方块内。通过这个行为，可以进行不一致的缩放。这就使得我们可以沿着中心点旋转手势，假设C和T_i之间的距离仅受旋转的影响。当然，不一致的缩放会带来一些限制。缩放后，将手势平移到引用点。

步骤4.找出最优的角度求得最高的分数

这里才是真正的识别步骤。使用等式1来将C与每一个模板T_i做对比，求出对应点之间的平均距离。

求出的路径差异最小的模板T就是目标模板。最小的路径差异d_i*被转换到[0,1]区间的分数段：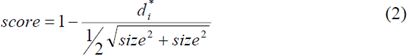

Size是步骤3中所提到的引用方块的一条边的长度。

有时候为了寻找最小的路径差异，可能会旋转手势找到全局最小的值。论文对大量例子做了分析，发现总存在一个全局最小，并且没有局部最小值的影响。

所以，首先用蛮力法，通过+1°和-1°来判断路径差异的增长。实验显示蛮力法总能找到最小值，一般旋转4.2°左右。但是，对于不相似的匹配来说，爬山法并不能获得准确的最小值。但这个不足为虑，因为这只让不正确的匹配更不容易被选中。不过这样会大大增加迭代时间，降低算法效率。因此论文采用GSS策略来寻找局部最小值，使用的是黄金分割率。

论文在最后附上了详尽的伪代码，实现毫无压力。这个方法的缺点是识别一维的手势不是很好，因为在scale的过程中，所有的笔画都被映射到size*size的方块内，一维手势必然会走样。而且论文无法区分方向性的手势，并且好的识别结果需要模板之间的差异性较大。

A Lightweight Multistroke Recognizer for User Interface Prototypes

这篇论文是对上一篇论文的改进，支持多笔画。论文为输入的多手势模板，生成多种组合的模板进行匹配。但这将降低算法的效率，对于生成了i个笔画的手势共生成个模板。因此，论文做了一些优化，通过手势的起始角度来决定与哪个模板做匹配。起始角度的计算并不严密，只是计算了第一个点与第K个点的连线的角度（K为采样点数量除以8）。在论文的实验中发现，这样的结果是最好的。在识别的过程中，论文还通过手势的数量来进行筛选匹配。

算法可以设定界限旋转不变性，会在模板内标明该模板是否是方向相关的，然后设置一个旋转界限。这样就能够区分方向性的手势了。

由于$1算法无法区分水平线和垂直线，所以无法处理一维手势。需要在程序中设置flag来特别说明这是一个一维手势，才可以正确地识别。而这篇论文中的算法会根据手势的OBB包围盒的边长比率来自动区分一维和二维手势，然后分别进行缩放。如果比率小于一个阀值，就判定这个手势是1D的，在对其进行缩放的时候会保留方向。

这篇论文最后也附有伪代码。带在具体的实现过程中我做了一些修改，因为OBB的计算略为耗时，我用的是基于协方差矩阵的方法，速度下降了很多，后来被舍弃了。而且，多笔画手势的排列生成也许是因为我实现有问题，并没有得到应有的效果，还严重影响了效率，也被舍弃了。我仅仅改变了多笔画的顺序，生成i!个手势进行识别。

最后的识别率还不错，如果不往变态了画还是都能识别出来的，平均耗时在100ms以内。不过以前没写过JAVA，算法就没怎么优化过，应该还是有很大的提升空间的吧。