CCF编程能力等级认证GESP—C++8级—20250322

单选题（每题 2 分，共 30 分）

1、国家“以旧换新”政策仍在继续，小杨家决定在家里旧的冰箱、电视、洗衣机、微波炉中选两种换新。其中，冰箱有4种型号可选，电视有6种型号可选，洗衣机有3种型号可选，微波炉有5种型号可选。请问小杨家共有多少种换新的方案？（ ）。

A. 18
B. 119
C. 238
D. 360

正确答案：B

2、小杨和3位朋友约好一起去看电影“哪吒2”。打开购票软件，他们发现，已经没有同一排连续的四个座位了（图中每个方框代表一个座位，红色方框代表已经售出）。朋友们商量了一下，决定分为两组，每组两人在同一排的相邻两个座位，且两组之间至少有一对座位是前后相邻的。请问共有多少种购票方案？（ ）。

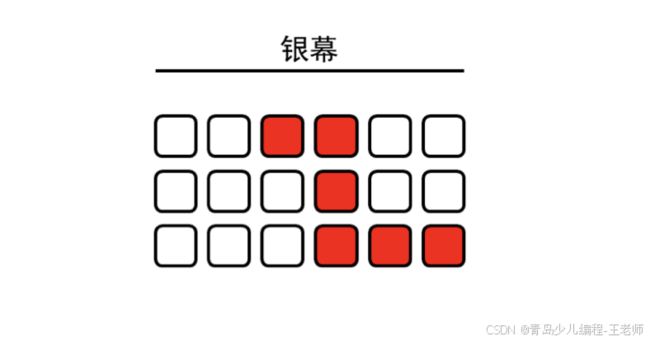
A. 495
B. 96
C. 7
D. 4

正确答案：C

3、下面关于C++类构造和析构函数的说法，错误的是（ ）。

A. 构造函数不能声明为虚函数。
B. 析构函数必须声明为虚函数。
C. 类的默认构造函数可以被声明为private。
D. 类的析构函数可以被声明为private。

正确答案：B

4、下列关于树和图的说法，错误的是（ ）

A. 树是一种有向无环图，有向无环图都是一棵树。
B. 如果把树看做有向图，每个节点指向其子节点，则该图是弱连通图。
C. N个顶点且连通的无向图，其最小生成树一定包含N - 1个条边。
D. N + 1个顶点、N条边的有向图，一定不是强连通的。

正确答案：A

5、从1到2025这2025个数中，包含数字5的个数（ ）。

A. 600
B. 601
C. 602
D. 603

正确答案：D

6、已定义 double 类型的变量 r 和 theta ，分别表示图中圆半径和圆心角。下列表达式中可以求出弦长 s 的是（ ）。

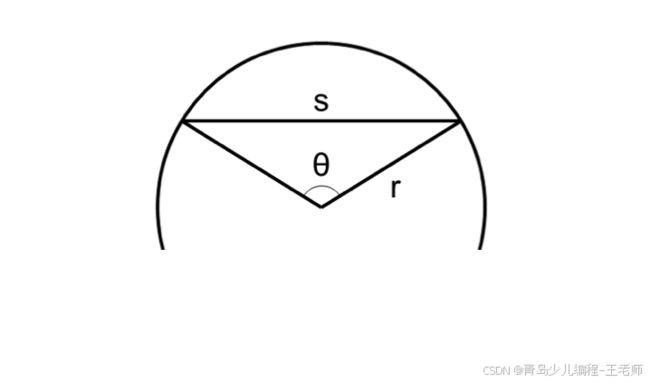
A. r * cos(theta)
B. r * cos(theta / 2) * 2
C. r * sin(theta)
D. r * sin(theta / 2) * 2

正确答案：D

7、 N个节点的平衡二叉树的高为（ ）。

A. $\lfloor lo{g}_{2}N\rfloor$
B. $\lceil lo{g}_{2}N\rceil$
C. $\lfloor lo{g}_{2}N\rfloor +1$
D. 无法确定
正确答案：D

8、下列关于算法的说法，错误的是（ ）。

A. 如果有足够的时间和空间，枚举法能解决一切有限的问题。
B. 分治算法将原问题分为多个子问题进行求解，且分解出的子问题必须相互独立。
C. 如果能找到合理的贪心原则，贪心算法往往能够比其他方法更快求解。
D. 倍增法在搜索未知长度的有序数组时，通过动态倍增或减半步长，快速定位目标范围。

正确答案：B

9、 2025是个神奇的数字，因为它是由两个数20和25拼接而成，而且$2025=(20+25{)}^2$。小杨决定写个程序找找小于N的正整数中共有多少这样神奇的数字。下面程序横线处应填入的是（ ）。

#include 
int count_miracle(int N) {
	int cnt = 0;
	for (int n = 1; n * n < N; n++) {
		int n2 = n * n;
		std::string s = std::to_string(n2);
		for (int i = 1; i < s.length(); i++)
			if (s[i] !='0') {
				std::string sl = s.substr(0, i);
				std::string sr = s.substr(i);
				int nl = std::stoi(sl);
				int nr = std::stoi(sr);
				if (_________) // 在此处填入选项
					cnt++;
			}
	}
	return cnt;
}

A. nl + nr == n
B. nl + nr == n2
C. (nl + nr) * (nl + nr) == n
D. (nl + nr) ^ 2 == n2

正确答案：A

10、2025是个神奇的数字，因为它是由两个数20和25拼接而成，而且$2025=(20+25{)}^2$。小杨决定写个程序找找小于N的正整数中共有多少这样神奇的数字。该函数的时间复杂度为（ ）。

#include 
int count_miracle(int N) {
	int cnt = 0;
	for (int n = 1; n * n < N; n++) {
		int n2 = n * n;
		std::string s = std::to_string(n2);
		for (int i = 1; i < s.length(); i++)
			if (s[i] !='0') {
				std::string sl = s.substr(0, i);
				std::string sr = s.substr(i);
				int nl = std::stoi(sl);
				int nr = std::stoi(sr);
				if (_________) // 在此处填入选项
					cnt++;
			}
	}
	return cnt;
}

A. $O(NlogN)$
B. $O(N^{1/2})$
C. $O(N^{1/2}logN)$
D. $O(N^{1/2}(logN{)}^2)$

正确答案：D

11、下面的欧氏筛法程序中，两个横线处应填入的分别是（ ）。

int primes[MAXP], num = 0;
bool isPrime[MAXN + 1] = {false};
void sieve() {
	for (int n = 2; n <= MAXN; n++) {
		if (!isPrime[n])
			primes[num++] = n;
		for (int i = 0; i < num &&________; i++) { // 在此处填入选项
			isPrime[n * primes[i]] = true;
			if (________) // 在此处填入选项
				break;
		}
	}
}

A.
n * primes[i] < MAXN
n % primes[i] == 0

B.
n * primes[i] < MAXN
primes[i] > n

C.
n * primes[i] <= MAXN
n % primes[i] == 0

D.
n * primes[i] <= MAXN
primes[i] > n

正确答案：C

12、下面Floyd算法中，横线处应该填入的是（ ）。

#include 
using namespace std;
#define N 21
#define INF 99999999
int map[N][N];
int main() {
	int n, m, t1, t2, t3;
	cin >> n >> m;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
		if (i == j)
			map[i][j] = 0;
		else
			map[i][j] = INF;
		}
	}
	for (int i = 1; i <= m; i++) {
		cin >> t1 >> t2 >> t3;
		map[t1][t2] = t3;
	}
	for (int k = 1; k <= n; k++)
		for (int i = 1; i <= n; i++)
			for (int j = 1; j <= n; j++)
				if (map[i][j] > map[i][k] + map[k][j])
					________; // 在此处填入选项
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			cout.width(4);
			cout << map[i][j];
		}
		cout << endl;
	}
}

A.map[i][j] = map[i][k] + map[k][j]
B.map[i][k] = map[i][j] - map[k][j]
C.map[i][j] = map[i][k] - map[k][j]
D.map[k][j] = map[i][j] - map[i][k]

正确答案：A

13、下面Floyd算法程序的时间复杂度为（ ）。

#include 
using namespace std;
#define N 21
#define INF 99999999
int map[N][N];
int main() {
	int n, m, t1, t2, t3;
	cin >> n >> m;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			if (i == j)
				map[i][j] = 0;
			else
				map[i][j] = INF;
		}
	}
	for (int i = 1; i <= m; i++) {
		cin >> t1 >> t2 >> t3;
		map[t1][t2] = t3;
	}
	for (int k = 1; k <= n; k++)
		for (int i = 1; i <= n; i++)
			for (int j = 1; j <= n; j++)
				if (map[i][j] > map[i][k] + map[k][j])
					________; // 在此处填入选项
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			cout.width(4);
			cout << map[i][j];
		}
		cout << endl;
	}
}

A. $O(N)$
B. $O(N^2)$
C. $O(N^3)$
D. $O(N^{2}logN)$

正确答案：C

14、下列程序实现了输出杨辉三角形，代码中横线部分应该填入的是（ ）。

#include 
using namespace std;
#define N 35
int a[N];
int main() {
	int n;
	cin >> n;
	for (int i = 0; i < n; i++) {
		a[i] = 1;
		for (int j = i - 1; j > 0; j--)
			________; // 在此处填入选项
		for (int j = 0; j <= i; j++)
			cout << a[j] << " ";
		cout << endl;
	}
	return 0;
}

A.a[j] += a[j + 1]
B.a[j] += a[j - 1]
C.a[j - 1] += a[j]
D.a[j + 1] += a[j]

正确答案：B

15、下列程序实现了输出杨辉三角形，其时间复杂度为（ ）。

#include 
using namespace std;
#define N 35
int a[N];
int main() {
	int n;
	cin >> n;
	for (int i = 0; i < n; i++) {
		a[i] = 1;
		for (int j = i - 1; j > 0; j--)
			________; // 在此处填入选项
		for (int j = 0; j <= i; j++)
			cout << a[j] << " ";
		cout << endl;
	}
	return 0;
}

A. $O(n)$
B. $O(nlogn)$
C. $O(n^2)$
D. $O(n^3)$

正确答案：C

判断题（每题 2 分，共 20 分）

1、表达式’5’ - 3.0 的结果为 2.0 ，类型为 double 。

正确答案：错误

2、在C++语言中，如果想要在一个函数内调用一个类的私有方法，可以在该类中将该函数声明为友元函数。

正确答案：正确

3、插入排序一般是稳定的。

正确答案：正确

4、5个相同的红球和4个相同的蓝球排成一排，要求蓝球不能相邻，则一共有15种排列方案。

正确答案：正确

5、使用 math.h 或 cmath 头文件中的函数，表达式 pow(2, 5) 的结果类型为 int 、值为 32 。

正确答案：错误

6、C++是一种面向对象编程语言，C则不是。多态是面向对象三大特性之一，虚函数是动态多态的代表特性。因此，使用C语言无法实现虚函数。

正确答案：错误

7、在N个节点的平衡二叉树中查找指定元素的最差时间复杂度为O(N)。

正确答案：错误

8、定义 int 类型的变量 a 和 b ，求二次函数$y=x^2+ax+b$取最小值时x的值，可以通过表达式-a / 2.0 求
得。

正确答案：正确

9、判断无向图中是否有环，可以通过广度优先搜索实现。

正确答案：正确

10、从32名学生中选出4人分别担任班长、副班长、学习委员和组织委员，共有C(32,4)种不同的选法。

正确答案：错误

编程题 (每题 25 分，共 50 分)

上学

【问题描述】
C 城可以视为由n个结点与m条边组成的无向图。这些结点依次以1,2, …,n标号，边依次以1,2, …, m标号。第i条边$（1\le i\le m）$连接编号为$u_i$与$v_i$的结点，长度为$l_i$米。
小 A 的学校坐落在 C 城中编号为s的结点。小 A 的同学们共有q位，他们想在保证不迟到的前提下，每天尽可能晚地出门上学。但同学们并不会计算从家需要多久才能到学校，于是找到了聪明的小 A。第i位同学$（1\le i\le q）$告诉小 A，他的家位于编号为$h_i$的结点，并且他每秒能行走 1 米。请你帮小 A 计算，每位同学从家出发需要多少秒才能到达学校呢？
【输入格式】
第一行，四个正整数n, m, s, q，分别表示 C 城的结点数与边数，学校所在的结点编号，以及小 A 同学们的数量。
接下来m行，每行三个正整数$u_i,v_i,l_i$，表示 C 城中的一条无向边。
接下来q行，每行一个正整数$h_i$，表示一位同学的情况。
【输出格式】
共q行，对于每位同学，输出一个整数，表示从家出发到学校的最短时间。
【样例输入 1】
5 5 3 3
1 2 3
2 3 2
3 4 1
4 5 3
1 4 2
5
1
4
【样例输出 1】
4
3
1
【数据范围】
对于20% 的测试点，保证 q = 1。
对于另外20% 的测试点，保证$1\le n\le 500,1\le m\le 500$。
对于所有测试点，保证$1\le n\le 2\times 10^5,1\le m\le 2\times 10^5,1\le q\le 2\times 10^5,1\le u_i,v_i,s,h_i\le n,1\le l_i\le 10^6$。
保证给定的图联通。

割裂

【问题描述】
小杨有一棵包含 个节点的树，其中节点的编号从1到n。
小杨设置了a个好点对$\{<u_1,v_1>,<u_2,v_2>,...,<u_a,v_a>,\}$和1个坏点对$<b_u,b_v>,$。一个节点能够被删除，当且仅当：

• 删除该节点后对于所有的$i(1\le i\le a)$，好点对$u_i$和$v_i$仍然连通；
• 删除该节点后坏点对 和 不连通。

如果点对中的任意一个节点被删除，其视为不连通。
小杨想知道，有多少个节点能够被删除。
【输入格式】
第一行包含两个正整数n, a，含义如题面所示。
之后n-1行，每行包含两个正整数$x_i,y_i$，代表存在一条连接节点$x_i$和$y_i$的边。
之后a行，每行包含两个正整数$u_1,v_1$，代表一个好点对$<u_i,v_i>$。
最后一行包含两个正整数$b_u,b_v$，代表坏点对$<b_u,b_v>$。
【输出格式】
输出一个正整数，代表能够删除的节点个数。
【样例输入 1】
6 2
1 3
1 5
3 6
3 2
5 4
5 4
5 3
2 6
【样例输出 1】
2
【数据范围】

子任务编号	分值	n	a
1	20%	10	0
2	20%	$\le 100$	$\le 100$
3	60%	$\le 10^6$	$\le 10^5$

对于全部数据，保证有$1\le n\le 10^6,0\le a\le 10^5,u_i\ne v_i,b_u\ne b_v$。