【蓝桥杯】版本分支 (图论——Tarjan求LCA)

一、算法介绍(Tarjan算法-离线求LCA )

1. 什么是最近共先祖 ？

首先是最近公共祖先的概念(什么是最近公共祖先？)：

在一棵没有环的树上，每个节点肯定有其父亲节点和祖先节点，而最近公共祖先，就是两个节点在这棵树上深度最大的公共的祖先节点。

换句话说，就是两个点在这棵树上距离最近的公共祖先节点。

所以LCA主要是用来处理当两个点仅有唯一一条确定的最短路径时的路径。

有人可能会问：那他本身或者其父亲节点是否可以作为祖先节点呢？

答案是肯定的，很简单，按照人的亲戚观念来说，你的父亲也是你的祖先，而LCA还可以将自己视为祖先节点。
　　　　
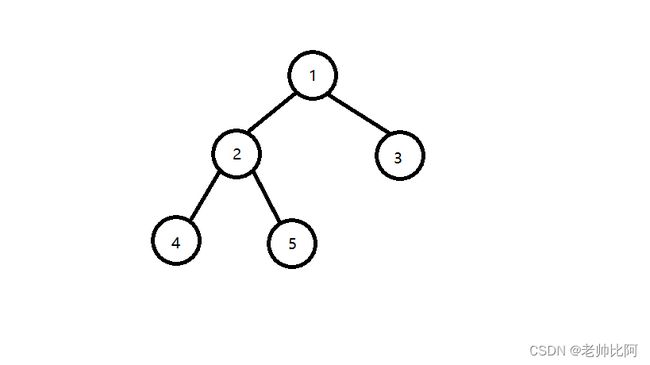
举个例子吧，如下图所示４和５的最近公共祖先是２，５和３的最近公共祖先是１，２和１的最近公共祖先是１。　

2.Tarjan算法

时间复杂度： O(n + m) ，n是结点的数量，m为询问查询的数量。Tarjan是离线算法，所谓离线就是不能边查询两个结点的公共祖先，只能把结点全部存起来，再来求。

算法思路：
tarjan算法其实就是我们在深度遍历是对结点进行分类处理，我们在对整颗树深搜时，会将所以点分为三类：这里我们用数字0，1，2来代替。（这个用一个st数组维护即可）
第0类，就是还没遍历过的结点。
第1类，就是在目前所遍历到的分支上的结点
第2类，就是已经遍历过的结点并且已经回溯完成。（他和第一类的区别在于结点已经回溯完成）。

那tarjan是如何来处理公共祖先问题的呢？这里需要借助一个数据结构——并查集。在遍历时我们需要记录下第2类结点的最近祖先。这样我们在遍历到每一个结点的时候，只需要来枚举一下当前结点存在哪些询问，如果存在一个询问的话，那么我们找到询问中对应的另一个结点，如果此时这个结点为第2类，那么并查集存的就是他们的祖先结点。
举个例子：假设我们现在遍历到u点，那么此时我们应该把u归为第一类（令st[u] = 1),接着我们枚举u的相邻结点，等我们回溯回来后，就可以来处理询问了，那么假设现在我们查找到一个询问，问u和v的最近公共祖先是谁。如果v结点为第二类，那么此时并查集中v的祖先结点就是他们两个的最近公共祖先。

上面例子理解起来不难，但是为什么这样就能确定并查集中v的祖先结点就是他们两个的最近公共祖先？

因为我们在深搜时，最近公共祖先必定是先被遍历到的，而并查集中的祖先结点也是离v最近的祖先结点，那么此时的话就会出现两种情况，第一种,如果在这个祖先结点下存在一对询问，最近公共祖先必然就是并查集中v的祖先结点。否则的话就是第二种情况：如果不存在，那么在随着回溯的进行，v的祖先结点也会因此被更新的更高一层。所以这个过程是并查集和回溯互补的过程，需要细细体会。

废话不多说，看下面例题吧。

二、例题

版本分支

题目描述
小明负责维护公司一个奇怪的项目。这个项目的代码一直在不断分支(branch)但是从未发生过合并(merge)。

现在这个项目的代码一共有 N 个版本，编号 1 ~ N，其中 1 号版本是最初的版本。

除了 1 号版本之外，其他版本的代码都恰好有一个直接的父版本；即这 N 个版本形成了一棵以 1 为根的树形结构。

如下图就是一个可能的版本树：

1

/ \

2 3

\ / \

5 4 6

现在小明需要经常检查版本 x 是不是版本 y 的祖先版本。你能帮助小明吗？

输入描述
第一行包含两个整数 N, QN,Q，代表版本总数和查询总数。

以下 NN - 1 行，每行包含 2 个整数 u 和 v ，代表版本 u 是版本 v 的直接父版本。

再之后 QQ 行，每行包含 2 个整数 x 和 y，代表询问版本 x 是不是版本 y 的祖先版本。

输出描述
对于每个询问，输出 YES 或 NO 代表 xx 是否是 yy 的祖先。

输入输出样例
输入
6 5
1 2
1 3
2 5
3 6
3 4
1 1
1 4
2 6
5 2
6 4
输出

YES
YES
NO
NO
NO
运行限制
最大运行时间：1s
最大运行内存: 256M
题目来源： 第九届蓝桥杯国赛
题目链接：版本分支

思路分析：
题意很简单，就是给我们两个结点x，y。问x是不是y的祖先结点。注意这里问的只是祖先结点，不是公共祖先。这个题目就是考察我们tarjan的回溯更新祖宗结点这个特性，这个做法其实很简单，首先我们存下询问，询问内容是，x结点是否是y的祖先结点，直接一遍tarjan算法，并且遍历到每个结点，在询问处理是，如果y的并查集中的父节点出现过x，那么则x就是y的祖先结点。

最后附上代码，输入内容很大，最好用scanf读入。

#include 
#include 
using namespace std;

typedef pair<int,int> PII;

const int N = 100010;

int p[N],st[N];

vector<PII> query[N];
vector<int> v[N];
bool res[N];

int Find(int x)
{
  if(p[x] != x) p[x] = Find(p[x]);
  return p[x];
}

void tarjan(int u)
{
    st[u] = 1;
    for (int i = 0; i < v[u].size(); i ++ )
    {
      int t = v[u][i];
      if(!st[t])
      {
          tarjan(t);
          p[t] = u;
      }
    }

    for (auto item : query[u])
    {
       int y = item.first,id = item.second;
       int anc = Find(y);
       if(anc == u) res[id] = true;
    }

    st[u] = 2;
}

int main()
{
  int n,m;
  scanf("%d%d",&n,&m);
  for (int i = 0; i < n - 1; i ++ )
  {
      int a,b;
      scanf("%d%d",&a,&b);
      v[a].push_back(b);
      v[b].push_back(a);
  }
  for (int i = 0; i < m; i ++ )
  {
      int a,b;
      scanf("%d%d",&a,&b);
      query[a].push_back({b,i});
  }
  for (int i = 1; i <= n; i ++ ) p[i] = i;
  tarjan(1);
  for (int i = 0; i < m; i ++ )
      if(res[i]) printf("YES\n");
      else printf("NO\n");
  return 0;
}

更多例题推荐：acwing距离

总结