【目标检测】【深度学习】【Pytorch版本】YOLOV3模型算法详解
【目标检测】【深度学习】【Pytorch版本】YOLOV3模型算法详解
文章目录
- 【目标检测】【深度学习】【Pytorch版本】YOLOV3模型算法详解
- 前言
- YOLOV3的模型结构
-
- YOLOV3模型的基本执行流程
- YOLOV3模型的网络参数
- YOLOV3的核心思想
-
- 前向传播阶段
- 反向传播阶段
- 总结
前言
YOLOV3是由华盛顿大学的Joseph Redmon等人在《YOLOv3: An Incremental Improvement》【论文地址】中提出的YOLO系列单阶段目标检测模型的升级改进版,核心思想是在YOLOV2基础上,通过引入多项关键技术和模块提升检测性能,即特征金字塔网络(FPN)结构的多尺度特征融合、更深的Darknet-53网络、借鉴了ResNet的残差连接设计、改进的损失函数等使得YOLOV3在保持高速的同时,大幅提升了检测精度。
Joseph Redmon在提出了YOLO三部曲之后,宣布退出计算机视觉研究,后续的YOLO系列是其他人在其基础上的创新改进。
YOLOV3的模型结构
YOLOV3模型的基本执行流程
下图是博主根据原论文绘制了YOLOV3模型流程示意图:
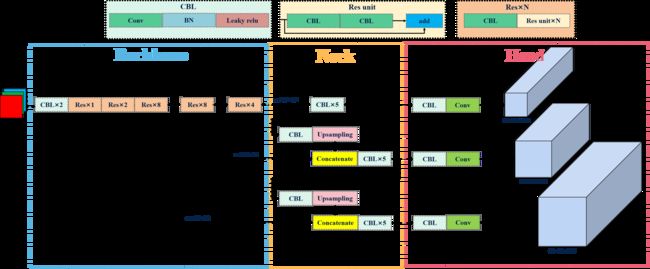
基本流程: 将输入图像调整为固定大小(416x416),使用Darknet-53作为骨干网络来提取图像的特征(包含了检测框位置、大小、置信度以及分类概率),在三个不同尺度特征图划分网格,每个单元网格负责预测一定数量的边界框及其对应的类别概率,分别对应于小、中、大尺寸目标的检测。
YOLOV3模型的网络参数
YOLOV3网络参数: YOLOV3采用的Darknet-53结构,由于没有全连接层,模型的输入可以是任意图片大小,不管是416×416还是320×320,因此可以进行多尺度训练。
53是指有53个Convolutional层。
YOLOV3的核心思想
前向传播阶段
特征金字塔(FPN): 包含了从底层到顶层的多个尺度的特征图,每个特征图都融合了不同层次的特征信息,每一层都对应一个特定的尺度范围,利用不同尺度的特征图进行检测,使得模型能够同时处理不同大小的目标【参考】 。

通过以下步骤实现多尺度特征的提取和融合:
- step1(自底向上): 使用基础网络(ResNet等)作为骨干网络(backbone),对输入图像中逐层提取特征,特征图的分辨率逐渐降低,按照输出特征图分辨率大小划分为不同的阶段(stage),相邻俩个阶段的特征图,后一个阶段相对于前一个阶段特征图尺度缩小一半,通道数则增加一倍;
- step2(自顶向下): 后一阶段的高层特征图上采样(up-sampling,通常采用2倍邻近插值算法),使其分辨率尺寸与前一阶段的低层特征图相匹配,;
- step3(横向连接): 将俩个特征图进行通道拼接,完成低层特征图的高分辨率信息与高层特征图的丰富语义信息的融合。
检测头: 基于多尺度特征图来预测目标的位置和类别,作用如下:
- 多尺度预测: 在三个不同尺度的特征图上分别应用检测头,使得模型可以同时处理小、中、大型目标的检测问题,有效地提高模型对不同尺寸目标的检测能力;
- 边界框预测: 每个检测头基于一组(3个)预选框(anchor boxes)负责预测边界框,预测预选框相对于真实框(ground truth)的偏移和缩放来确定边界框位置,预测框中目标存在的概率以及目标类别的概率来确定边界框的类别。
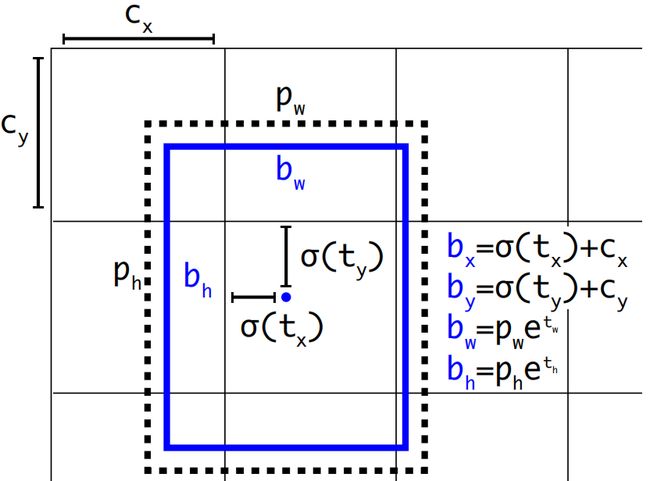
位置预测: YOLOV3延续了YOLOV2的设计,利用预选框来预测边界框相对预选框之间的误差补偿(offsets),预测边界框位置(中心点)在所属网格单元左上角位置进行相对偏移值,预测边界框尺寸基于所对应的预选框宽高进行相对缩放:
b x = σ ( t x ) + c x b y = σ ( t y ) + c y b w = p w e t w b h = p h e t h \begin{array}{l} {b_x} = \sigma ({t_x}) + {c_x}\\ {b_y} = \sigma ({t_y}) + {c_y}\\ {b_w} = {p_w}{e^{{t_w}}}\\ {b_h} = {p_h}{e^{{t_h}}} \end{array} bx=σ(tx)+cxby=σ(ty)+cybw=pwetwbh=pheth
使用sigmoid函数处理偏移值,将边界框中心点约束在所属网格单元中,网格单元的尺度为1,而偏移值在(0,1)范围内,防止过度偏移。
( c x , c y ) ({c_x},{c_y}) (cx,cy)是网格单元的左上角坐标, p w p_w pw和 p h p_h ph是预选框的宽度与高度, e t w e^{{t_w}} etw和 e t h e^{{t_h}} eth则没有过多约束是因为物体的大小是不受限制的。
多尺度训练: 采用不同分辨率的多尺度图像训练(输入图像尺寸动态变化),让模型能够鲁棒地运行在不同尺寸的图像上,提高了模型对不同尺寸目标的泛化能力 。
数据正负样本: 、 预测框分为三 种情况::正样本(positive)、负样本(negative)和忽略样本(ignore)。
-
正样本: 任取一个真实框,计算与其类别相同的全部预测框IOU,IOU最大的预测框作为正样本,正样本IOU可能小于阈值。一个预测框只分配给一个真实框。正样本产生置信度loss、检测框loss以及类别loss,真实框的类别标签是onehot编码,置信度标签为1。
当前真实框已经匹配了一个预测框,那么下一个真实框就在余下的预测框中匹配IOU最大的作为其正样本。
-
忽略样本: 与任意一个真实框IOU大于阈值但没成为正样本的预测框,就是忽略样本。忽略样样本不产生任何loss。
-
负样本: 任取一个真实框,计算与其类别相同的全部预测框IOU,IOU小于阈值的预测框作为负样本。负样本只产生置信度loss、真实框的置信度标签为0。
根据上述标准,下图中以检测狗为例,浅绿色是真实框,绿色是正样本预测框,橙色是忽略样本预测框,红色则是负样本预测框。
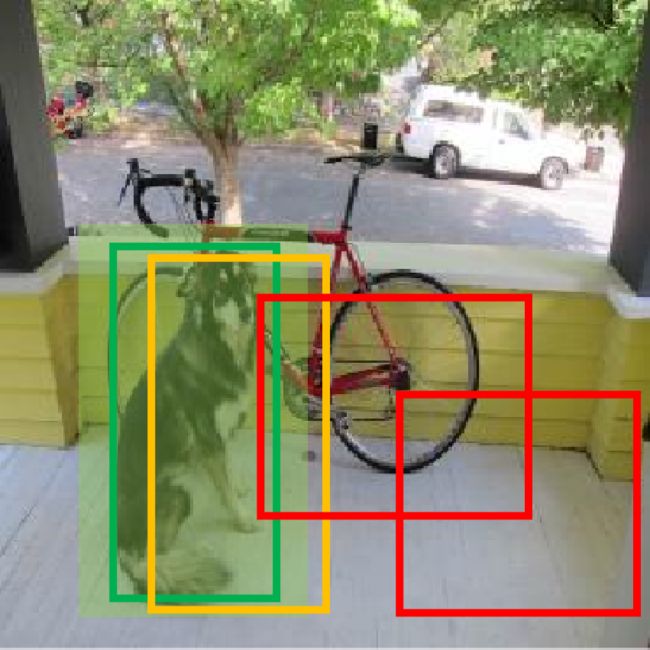
在之前的YOLO版本中,正样本使用真实框与预测框的IOU作为置信度,置信度始终比较小,检测的召回率不高(过滤太多找不全),特别是在学习小物体时,IOU可能更小,导致无法有效学习。YOLOV3将正样本置信度设置为1,因为置信度本身就是二分类问题,即预测框中是不是一个真实物体,标签是1或0更加合理。
反向传播阶段
损失函数: YOLOV3的损失函数公式为:
L o s s = − λ c o o r d ∑ i = 0 S 2 ∑ j = 0 B 1 i j o b j [ x ∧ i j log ( x i j ) + ( 1 − x ∧ i j ) log ( 1 − x i j ) + y ∧ i j log ( y i j ) + ( 1 − y ∧ i j ) log ( 1 − y i j ) ] + 1 2 λ c o o r d ∑ i = 0 S 2 ∑ j = 0 B 1 i j o b j [ ( w i j − w ∧ i j ) 2 + ( h i j − h ∧ i j ) 2 ] − ∑ i = 0 S 2 ∑ j = 0 B 1 i j o b j [ C ∧ i j log ( C i j ) + ( 1 − C ∧ i j ) log ( 1 − C i j ) ] − λ n o o b j ∑ i = 0 S 2 ∑ j = 0 B 1 i j n o o b j [ C ∧ i j log ( C i j ) + ( 1 − C ∧ i j ) log ( 1 − C i j ) ] − ∑ i = 0 S 2 ∑ j = 0 B 1 i j o b j ∑ c ∈ c l a s s e s [ P ∧ i j c log ( P i j c ) + ( 1 − P ∧ i j c ) log ( 1 − P i j c ) ] L{\rm{oss}} = - {\lambda _{coord}}\sum\limits_{i = 0}^{{S^2}} {\sum\limits_{j = 0}^B {1_{ij}^{obj}\left[ {{{\mathop x\limits^ \wedge }_{ij}}\log ({x_{ij}}) + (1 - {{\mathop x\limits^ \wedge }_{ij}})\log (1 - {x_{ij}}) + {{\mathop y\limits^ \wedge }_{ij}}\log ({y_{ij}}) + (1 - {{\mathop y\limits^ \wedge }_{ij}})\log (1 - {y_{ij}})} \right]} } + \frac{1}{2}{\lambda _{coord}}\sum\limits_{i = 0}^{{S^2}} {\sum\limits_{j = 0}^B {1_{ij}^{obj}\left[ {{{({w_{ij}} - {{\mathop w\limits^ \wedge }_{ij}})}^2} + {{({h_{ij}} - {{\mathop h\limits^ \wedge }_{ij}})}^2}} \right]} } - \sum\limits_{i = 0}^{{S^2}} {\sum\limits_{j = 0}^B {1_{ij}^{obj}\left[ {{{\mathop C\limits^ \wedge }_{ij}}\log ({C_{ij}}) + (1 - {{\mathop C\limits^ \wedge }_{ij}})\log (1 - {C_{ij}})} \right]} } - {\lambda _{noobj}}\sum\limits_{i = 0}^{{S^2}} {\sum\limits_{j = 0}^B {1_{ij}^{noobj}\left[ {{{\mathop C\limits^ \wedge }_{ij}}\log ({C_{ij}}) + (1 - {{\mathop C\limits^ \wedge }_{ij}})\log (1 - {C_{ij}})} \right]} - \sum\limits_{i = 0}^{{S^2}} {\sum\limits_{j = 0}^B {1_{ij}^{obj}\sum\limits_{c \in classes} {\left[ {{{\mathop P\limits^ \wedge }_{ijc}}\log ({P_{ijc}}) + (1 - {{\mathop P\limits^ \wedge }_{ijc}})\log (1 - {P_{ijc}})} \right]} } } } Loss=−λcoordi=0∑S2j=0∑B1ijobj[x∧ijlog(xij)+(1−x∧ij)log(1−xij)+y∧ijlog(yij)+(1−y∧ij)log(1−yij)]+21λcoordi=0∑S2j=0∑B1ijobj[(wij−w∧ij)2+(hij−h∧ij)2]−i=0∑S2j=0∑B1ijobj[C∧ijlog(Cij)+(1−C∧ij)log(1−Cij)]−λnoobji=0∑S2j=0∑B1ijnoobj[C∧ijlog(Cij)+(1−C∧ij)log(1−Cij)]−i=0∑S2j=0∑B1ijobjc∈classes∑[P∧ijclog(Pijc)+(1−P∧ijc)log(1−Pijc)]
- ∑ i = 0 S 2 \sum\limits_{{\rm{i}} = 0}^{{S^2}} {} i=0∑S2表示遍历所有网格单元并进行累加;
- ∑ j = 0 B \sum\limits_{{\rm{j}} = 0}^B {} j=0∑B表示遍历所有预测边界框并进行累加。
预测框位置损失: 计算了所有预测框的位置(中心坐标)与真实框的位置的交叉熵误差损失和。
− λ c o o r d ∑ i = 0 S 2 ∑ j = 0 B 1 i j o b j [ x ∧ i j log ( x i j ) + ( 1 − x ∧ i j ) log ( 1 − x i j ) + y ∧ i j log ( y i j ) + ( 1 − y ∧ i j ) log ( 1 − y i j ) ] - {\lambda _{coord}}\sum\limits_{i = 0}^{{S^2}} {\sum\limits_{j = 0}^B {1_{ij}^{obj}\left[ {{{\mathop x\limits^ \wedge }_{ij}}\log ({x_{ij}}) + (1 - {{\mathop x\limits^ \wedge }_{ij}})\log (1 - {x_{ij}}) + {{\mathop y\limits^ \wedge }_{ij}}\log ({y_{ij}}) + (1 - {{\mathop y\limits^ \wedge }_{ij}})\log (1 - {y_{ij}})} \right]} } −λcoordi=0∑S2j=0∑B1ijobj[x∧ijlog(xij)+(1−x∧ij)log(1−xij)+y∧ijlog(yij)+(1−y∧ij)log(1−yij)]
- ( x ∧ i j , y ∧ i j ) {({{\mathop {{\rm{ }}x}\limits^ \wedge }_{ij}},{{\mathop {{\rm{ y}}}\limits^ \wedge }_{ij}})} (x∧ij,y∧ij)表示真实框的中心点坐标;
- ( x i j , y i j ) {({x_{ij}},{y_{ij}})} (xij,yij)表示预测框的中心点坐标;
- λ c o o r d {\lambda _{coord}} λcoord表示协调系数, λ c o o r d = ( 2 − w i j ∧ h i j ∧ ) {\lambda _{coord}} = (2 - {\mathop w\limits^ \wedge _{ij}}{\mathop h\limits^ \wedge _{ij}}) λcoord=(2−ijw∧ijh∧)协调检测目标不同大小对误差函数的影响:检测目标比较小时增大其对损失函数的影响,相反检测目标比较大时消减其对损失函数的影响;
- 1 i j o b j {1_{ij}^{obj}} 1ijobj表示当前预测框是否预测一个目标物体,如果预测一个目标则为1,否则等于0。
预测框尺度损失: 计算了所有预测框的宽高与真实框的宽高求和平方误差损失和。
1 2 λ c o o r d ∑ i = 0 S 2 ∑ j = 0 B 1 i j o b j [ ( w i j − w ∧ i j ) 2 + ( h i j − h ∧ i j ) 2 ] \frac{1}{2}{\lambda _{coord}}\sum\limits_{i = 0}^{{S^2}} {\sum\limits_{j = 0}^B {1_{ij}^{obj}\left[ {{{({w_{ij}} - {{\mathop w\limits^ \wedge }_{ij}})}^2} + {{({h_{ij}} - {{\mathop h\limits^ \wedge }_{ij}})}^2}} \right]} } 21λcoordi=0∑S2j=0∑B1ijobj[(wij−w∧ij)2+(hij−h∧ij)2]
- ( w ∧ i j , h ∧ i j ) {({{\mathop {{\rm{ }}w}\limits^ \wedge }_{ij}},{{\mathop {{\rm{ h}}}\limits^ \wedge }_{ij}})} (w∧ij,h∧ij)表示真实框的中心点坐标;
- ( w i j , h i j ) {({w_{ij}},{h_{ij}})} (wij,hij)表示预测框的中心点坐标。
预测框置信度损失: 计算了所有预测框的置信度与真实框的置信度的交叉熵误差损失和。
− ∑ i = 0 S 2 ∑ j = 0 B 1 i j o b j [ C ∧ i j log ( C i j ) + ( 1 − C ∧ i j ) log ( 1 − C i j ) ] − λ n o o b j ∑ i = 0 S 2 ∑ j = 0 B 1 i j n o o b j [ C ∧ i j log ( C i j ) + ( 1 − C ∧ i j ) log ( 1 − C i j ) ] - \sum\limits_{i = 0}^{{S^2}} {\sum\limits_{j = 0}^B {1_{ij}^{obj}\left[ {{{\mathop C\limits^ \wedge }_{ij}}\log ({C_{ij}}) + (1 - {{\mathop C\limits^ \wedge }_{ij}})\log (1 - {C_{ij}})} \right]} } - {\lambda _{noobj}}\sum\limits_{i = 0}^{{S^2}} {\sum\limits_{j = 0}^B {1_{ij}^{noobj}\left[ {{{\mathop C\limits^ \wedge }_{ij}}\log ({C_{ij}}) + (1 - {{\mathop C\limits^ \wedge }_{ij}})\log (1 - {C_{ij}})} \right]} } −i=0∑S2j=0∑B1ijobj[C∧ijlog(Cij)+(1−C∧ij)log(1−Cij)]−λnoobji=0∑S2j=0∑B1ijnoobj[C∧ijlog(Cij)+(1−C∧ij)log(1−Cij)]
- C ∧ i j {{{\mathop C\limits^ \wedge }_{ij}}} C∧ij表示真实框的置信度,包含检测目标取值为1,否则还是0;
- C i j {{C_{ij}}} Cij表示预测框的置信度;
- λ n o o b j {\lambda _{noobj}} λnoobj表示预测框没有目标的权重系数,通常大部分预测框都不包含检测目标物体,导致模型预测倾向于预测框中没有目标物体,因此必须减少没有目标物体的预测框的损失权重。
预测框类别损失: 计算了所有预测框的类别概率与真实框的类别概率的交叉熵误差损失和。
− ∑ i = 0 S 2 ∑ j = 0 B 1 i j o b j ∑ c ∈ c l a s s e s [ P ∧ i j c log ( P i j c ) + ( 1 − P ∧ i j c ) log ( 1 − P i j c ) ] - \sum\limits_{i = 0}^{{S^2}} {\sum\limits_{j = 0}^B {1_{ij}^{obj}\sum\limits_{c \in classes} {\left[ {{{\mathop P\limits^ \wedge }_{ijc}}\log ({P_{ijc}}) + (1 - {{\mathop P\limits^ \wedge }_{ijc}})\log (1 - {P_{ijc}})} \right]} } } −i=0∑S2j=0∑B1ijobjc∈classes∑[P∧ijclog(Pijc)+(1−P∧ijc)log(1−Pijc)]
- P ∧ i j c {{{\mathop P\limits^ \wedge }_{ijc}}} P∧ijc表示真实框的类别概率,onehot编码,所属的类别概率为1,其他类概率为0;
- P i j c {{P_{ijc}}} Pijc表示预测框的类别概率。
在YOLOV1和YOLOV2利用softmax来进行概率预测,这种激活函数让所有类别的概率相加等于1,因此只能进行单一分类预测,而在YOLOV3中将softmax修改成sigmoid函数,对不同类别单独进行二分类概率预测,因此进行多标签类别的分类预测。
YOLOV3可以同时是动物和猪俩类(sigmoid函数),而不是动物和猪中选择概括最大的一类(softmax函数)。
总结
尽可能简单、详细的介绍了YOLOV3模型的结构,深入讲解了YOLOV3核心思想。
