Python 递归竟然如何简单？ 看完此文。秒懂Python递归！！！

1. Python 递归

递归是一种解决问题的方法，其中一个函数调用其自身来解决更小的子问题。递归常用于解决那些可以分解成相似子问题的问题，比如树的遍历、排序、组合、求阶乘等问题。

---

1.1. 递归的定义

递归是指函数在执行过程中调用自身的一种编程技术。在递归调用过程中，函数会不断地分解问题，直到达到某个基本情况（也称为递归终止条件），然后逐步返回最终的结果。

递归可以分为两部分：

• 递归函数调用：函数通过调用自身来处理较小的子问题。
• 基本情况（终止条件）：定义递归的边界条件，防止无限递归。

示例：

计算阶乘是递归问题的经典示例。

# 阶乘的递归实现
def factorial(n):
    if n == 0:
        return 1  # 基本情况
    return n * factorial(n - 1)  # 递归调用

print(factorial(5))  # 输出: 120

在这个例子中，factorial 函数调用自身来计算更小的阶乘，直到达到基本情况 n == 0。

---

1.2. 递归的特征

递归具有以下几个显著特征：

1. 递归调用：

   • 递归函数会调用自身，直到满足某个终止条件。每次调用都会处理更小规模的子问题。

2. 基本情况（终止条件）：

   • 递归必须有一个基本情况，当满足条件时，递归将停止并返回结果。没有基本情况会导致无限递归，最终导致栈溢出。

3. 分解问题：

   • 递归通过将一个复杂的问题分解成更简单、更小的子问题来解决。例如，计算阶乘 factorial(n) 可以分解为 n * factorial(n-1)。

4. 自我调用：

   • 递归函数在其内部调用自身以逐步解决问题。每次递归调用都处理问题的一部分，直到达到基准条件。

示例：树的递归遍历

# 二叉树的递归遍历
class Node:
    def __init__(self, value):
        self.value = value
        self.left = None
        self.right = None

def in_order_traversal(root):
    if root:
        in_order_traversal(root.left)  # 递归遍历左子树
        print(root.value, end=" ")     # 访问当前节点
        in_order_traversal(root.right) # 递归遍历右子树

# 创建二叉树
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)

# 输出: 4 2 5 1 3
in_order_traversal(root)

---

1.3. 从零书写递归的思路

在编写递归函数时，通常可以遵循以下思路：

1. 确定递归的基本情况（终止条件）：

   • 在递归函数中，必须明确什么时候停止递归。通常这是一个边界条件，如 n == 0、n == 1 等。

2. 将问题分解成更小的子问题：

   • 递归通过将原问题分解为更小的子问题来求解。每次递归调用时，问题规模应该减小，直到达到基本情况。

3. 定义递归的函数结构：

   • 递归函数的结构应该是：首先判断是否满足基本情况，如果是则返回结果；如果不是，则递归调用自身并处理子问题。

4. 小心避免无限递归：

   • 每次递归时，确保递归参数朝着基本情况逼近，避免进入无限循环。可以通过检查递归参数的范围来保证递归的正确性。

递归问题的思考过程

以计算阶乘为例，思考过程可以如下：

• 问题：计算 n!（阶乘），即 n * (n-1) * ... * 1。
• 基本情况：当 n == 0 或 n == 1 时，阶乘为 1。
• 分解子问题：n! = n * (n-1)!。

根据上述思路，递归实现可以如下：

def factorial(n):
    if n == 0:  # 基本情况
        return 1
    return n * factorial(n - 1)  # 递归调用

print(factorial(5))  # 输出: 120

---

1.4. 什么场景适合使用递归

递归适用于以下几种类型的场景：

1. 分治问题：

   • 如果一个问题可以分解成多个相同结构的子问题并且每个子问题的解决方式与原问题相似，那么可以考虑使用递归。例如，快速排序、归并排序、二分查找等。

2. 树形结构遍历：

   • 树形结构的遍历问题适合使用递归，因为每个子树的结构和整个树相似。二叉树、N叉树等都适合用递归来进行遍历。

3. 图的深度优先搜索（DFS）：

   • 递归在图的遍历（如深度优先搜索）中非常有用，通过递归访问节点的邻居来遍历图的所有节点。

4. 回溯问题：

   • 回溯问题，如排列组合、数独、迷宫求解等，通常可以通过递归来解决。递归不断尝试不同的选择，并在遇到错误时回退。

5. 数学问题：

   • 计算阶乘、斐波那契数列、最大公约数等数学问题，递归提供了非常简洁的解决方式。

示例：斐波那契数列的递归实现

# 斐波那契数列递归实现
def fibonacci(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    return fibonacci(n - 1) + fibonacci(n - 2)

print(fibonacci(5))  # 输出: 5

---

2. 递归的典型案例以及思路讲解

递归是一种强大的技术，广泛应用于各种问题的求解。递归通过自我调用的方式将问题逐步简化，最终达到解决问题的目的。以下是几个典型的递归案例以及相应的思路讲解，帮助更好地理解递归的使用。

---

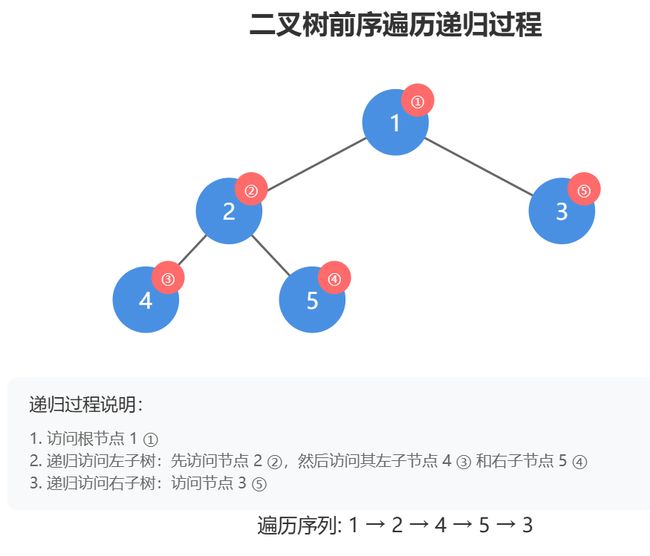
2.1. 二叉树的前序遍历 思路讲解

二叉树的前序遍历是递归应用的经典场景。前序遍历的规则是：首先访问根节点，然后遍历左子树，最后遍历右子树。

思路分析：

• 递归终止条件：当节点为空时，递归结束。
• 递归步骤：对于每个节点，首先访问当前节点，然后递归遍历左子树，最后递归遍历右子树。

前序遍历过程：

1. 访问根节点。
2. 遍历左子树。
3. 遍历右子树。

代码实现：

class Node:
    def __init__(self, value):
        self.value = value
        self.left = None
        self.right = None

def preorder_traversal(root):
    if root is None:
        return
    print(root.value, end=" ")  # 访问当前节点
    preorder_traversal(root.left)  # 递归遍历左子树
    preorder_traversal(root.right)  # 递归遍历右子树

# 创建二叉树
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)

# 输出：1 2 4 5 3
preorder_traversal(root)

思路总结：

• 递归的核心在于“先访问根节点，然后遍历左子树，再遍历右子树”。
• 通过递归调用，左子树和右子树的遍历过程也会按照同样的顺序进行，直到遍历完所有节点。

---

2.2. 目录树的思路讲解

目录树也是递归的经典应用。每个目录可能包含多个子目录和文件，通过递归地遍历每个子目录，可以实现整个目录树的遍历。

思路分析：

• 递归终止条件：当目录为空时，递归结束。
• 递归步骤：对于每个目录，首先访问当前目录，然后递归地遍历当前目录中的每个子目录和文件。

目录树遍历过程：

4. 遍历当前目录。
5. 遍历当前目录中的每个子目录。
6. 遍历当前目录中的文件（如果有）。

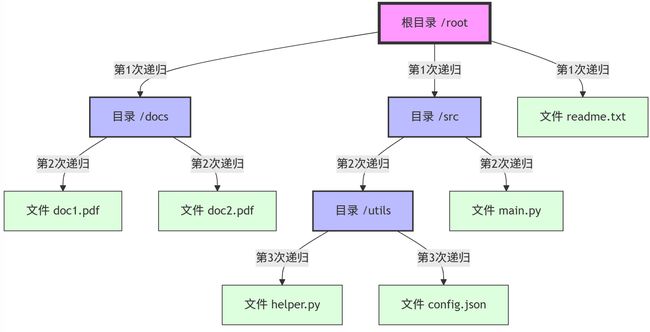
这个目录树图展示了递归遍历的完整过程，：

1. 第1次递归：
   • 从根目录 /root 开始
   • 发现三个项目：两个目录（/docs、/src）和一个文件（readme.txt）
   • 处理文件，继续递归遍历目录
2. 第2次递归：
   • 进入 /docs 目录
     • 发现两个文件（doc1.pdf、doc2.pdf）
     • 因为都是文件，这个分支的递归结束
   • 进入 /src 目录
     • 发现一个目录（/utils）和一个文件（main.py）
     • 处理文件，继续递归遍历目录
3. 第3次递归：
   • 进入 /utils 目录
     • 发现两个文件（helper.py、config.json）
     • 因为都是文件，递归结束

递归的关键特点：

• 每次进入新目录时，都会重复相同的处理逻辑
• 遇到文件就处理，遇到目录就继续递归
• 直到所有路径都被访问过，递归自然结束

这个过程就像是在探索一棵树，从顶部开始，沿着每个分支向下遍历，直到达到叶子节点（文件）。每个目录节点都会触发一次新的递归调用，而文件节点则是递归的终止点。

代码实现（模拟目录树）：

import os

def list_directory_tree(path):
    if not os.path.isdir(path):
        return
    print(f"目录: {path}")
    for item in os.listdir(path):
        full_path = os.path.join(path, item)
        if os.path.isdir(full_path):
            list_directory_tree(full_path)  # 递归遍历子目录
        else:
            print(f"文件: {full_path}")

# 输出当前目录及其子目录内容
list_directory_tree(".")

思路总结：

• 递归的关键在于“遍历当前目录，再递归遍历每个子目录”。
• 通过递归调用，目录树的结构逐步被展开，直到遍历完整个树。

---

2.3. 斐波那契数列思路详解

斐波那契数列是一个经典的递归问题，定义如下：F(0) = 0, F(1) = 1, F(n) = F(n-1) + F(n-2)。

思路分析：

• 递归终止条件：当 n == 0 或 n == 1 时，返回对应的值 0 或 1。
• 递归步骤：对于每个 n，计算 F(n) 的值为 F(n-1) 和 F(n-2) 的和。

斐波那契数列递归过程：

4. 对于 n == 0 或 n == 1，直接返回 0 或 1。
5. 对于其他情况，递归调用 fibonacci(n-1) 和 fibonacci(n-2) 并返回它们的和。

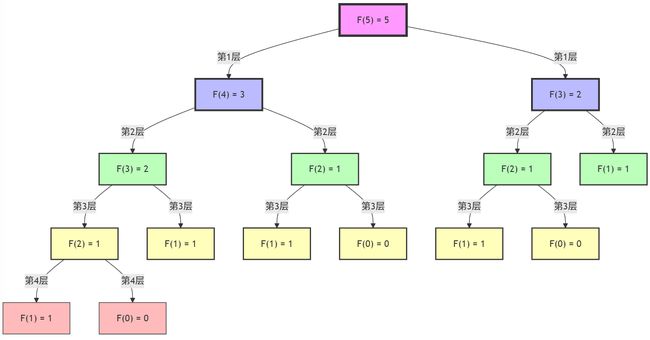
这个递归树展示了计算 F(5) 的完整过程。让我解释一下计算过程：

1. 第1层（根节点）：
   • F(5) 分解为计算 F(4) 和 F(3)
2. 第2层：
   • F(4) 分解为 F(3) 和 F(2)
   • F(3) 分解为 F(2) 和 F(1)
3. 第3层：
   • 继续分解，很多节点已经到达基本情况
   • 注意 F(2) 和 F(3) 被重复计算了多次
4. 第4层：
   • 大多数节点都是基本情况 F(1) = 1 或 F(0) = 0
   • 从这里开始可以向上回溯计算结果

图中的颜色编码：

• 粉红色：第1层（起始节点）
• 蓝色：第2层递归
• 绿色：第3层递归
• 黄色：第4层递归
• 红色：最深层递归

代码实现：

def fibonacci(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    return fibonacci(n - 1) + fibonacci(n - 2)

print(fibonacci(5))  # 输出: 5

思路总结：

• 递归的核心在于通过 F(n-1) 和 F(n-2) 的递归调用来计算 F(n) 的值。
• 递归是直观的，但效率较低，特别是对于较大的 n 值。每次计算都重复了很多子问题的计算。

优化：使用记忆化（Memoization）：

递归会导致大量重复计算，因此可以通过记忆化来优化性能。

def fibonacci(n, memo={}):
    if n in memo:
        return memo[n]
    if n == 0:
        return 0
    elif n == 1:
        return 1
    memo[n] = fibonacci(n - 1, memo) + fibonacci(n - 2, memo)
    return memo[n]

print(fibonacci(50))  # 输出: 12586269025

通过使用缓存（memo），重复计算的子问题会被存储，显著提高了计算效率。