二叉树的应用详解 - 数据结构
概述:
平衡树——特点:所有结点左右子树深度差≤1
排序树——特点:所有结点“左小右大字典树——由字符串构成的二叉排序树
判定树——特点:分支查找树(例如12个球如何只称3次便分出轻重)
带权树——特点:路径带权值(例如长度)
最优树——是带权路径长度最短的树,又称 Huffman树,用途之一是通信中的压缩编码。
1. 二叉排序树(二叉查找树 Binary Search Tree):
1.1 二叉排序树:
或是一棵空树;或者是具有如下性质的非空二叉树:
(1)若左子树不为空,左子树的所有结点的值均小于根的值;
(2)若右子树不为空,右子树的所有结点均大于根的值;
(3)它的左右子树也分别为二叉排序树。
例:二叉排序树 如图9.7:
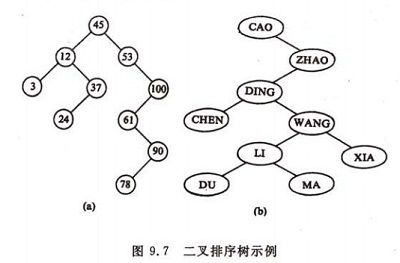
二叉排序树的查找过程和次优二叉树类似,通常采取二叉链表作为二叉排序树的存储结构。中序遍历二叉排序树可得到一个关键字的有序序列,一个无序序列可以通过构造一棵二叉排序树变成一个有序序列,构造树的过程即为对无序序列进行排序的过程。每次插入的新的结点都是二叉排序树上新的叶子结点,在进行插入操作时,不必移动其它结点,只需改动某个结点的指针,由空变为非空即可。搜索,插入,删除的复杂度等于树高,期望O(logn),最坏O(n)(数列有序,树退化成线性表).
虽然二叉排序树的最坏效率是O(n),但它支持动态查询,且有很多改进版的二叉排序树可以使树高为O(logn),如SBT,AVL,红黑树等.故不失为一种好的动态排序方法.
2.2 二叉排序树b中查找
在二叉排序树b中查找x的过程为:
- 若b是空树,则搜索失败,否则:
- 若x等于b的根节点的数据域之值,则查找成功;否则:
- 若x小于b的根节点的数据域之值,则搜索左子树;否则:
- 查找右子树。
2.3 在二叉排序树插入结点的算法
向一个二叉排序树b中插入一个结点s的算法,过程为:
- 若b是空树,则将s所指结点作为根结点插入,否则:
- 若s->data等于b的根结点的数据域之值,则返回,否则:
- 若s->data小于b的根结点的数据域之值,则把s所指结点插入到左子树中,否则:
- 把s所指结点插入到右子树中。
/*当二叉排序树T中不存在关键字等于e.key的数据元素时,插入e并返回TRUE,否则返回FALSE*/
Status InsertBST(BiTree &T, ElemType e){
if(!SearchBST(T, e.key, NULL,p){
s=(BiTree)malloc(sizeof(BiTNode));
s->data = e; s->lchild = s->rchild = NULL;
if(!p) T-s; //被插结点*s为新的根结点
else if LT(e.key, p->data.key) p->lchld = s; //被子插结点*s为左孩子
else p->rchild = s; //被插结点*s为右孩子
return TRUE;
}
else return FALSE; //树中已有关键字相同的结点,不再插入
}
2.4 在二叉排序树删除结点的算法
在二叉排序树删去一个结点,分三种情况讨论:
- 若*p结点为叶子结点,即PL(左子树)和PR(右子树)均为空树。由于删去叶子结点不破坏整棵树的结构,则只需修改其双亲结点的指针即可。
- 若*p结点只有左子树PL或右子树PR,此时只要令PL或PR直接成为其双亲结点*f的左子树即可,作此修改也不破坏二叉排序树的特性。
- 若*p结点的左子树和右子树均不空。在删去*p之后,为保持其它元素之间的相对位置不变,可按中序遍历保持有序进行调整,可以有两种做法:其一是令*p的左子树为*f的左子树,*s为*f左子树的最右下的结点,而*p的右子树为*s的右子树;其二是令*p的直接前驱(或直接后继)替代*p,然后再从二叉排序树中删去它的直接前驱(或直接后继)。在二叉排序树上删除一个结点的算法如下:
2. 5二叉排序树性能分析
每个结点的Ci为该结点的层次数。最坏情况下,当先后插入的关键字有序时,构成的二叉排序树蜕变为单支树,树的深度为n,其平均查找长度为 (和顺序查找相同),最好的情况是二叉排序树的形态和折半查找的判定树相同,其平均查找长度和log2(n)成正比 (O(log2(n)))。
(和顺序查找相同),最好的情况是二叉排序树的形态和折半查找的判定树相同,其平均查找长度和log2(n)成正比 (O(log2(n)))。
Size Balanced Tree(SBT)
AVL树
红黑树
Treap(Tree+Heap)
这些均可以使查找树的高度为O(logn)
2. 平衡树二叉树)(又称AVL 树):
1. 1 平衡二叉树(Balanced Binary Tree)
性质: 左右子树都是平衡二叉树且所有结点左、右子树深度之差的绝对值 ≤ 1。
若定义结点的“平衡因子” BF(Balance Factor) = 左子树深度 –右子树深度 则:平衡二叉树中所有结点的BF ∈[ -1, 0, 1 ]
例:判断下列二叉树是否AVL树?
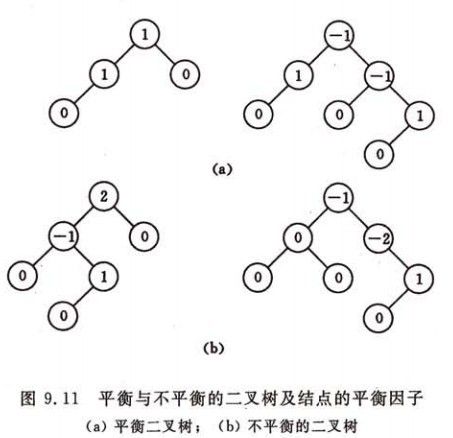
常用算法有红黑树、AVL、Treap、伸展树等。在平衡二叉搜索树中,我们可以看到,其高度一般都良好地维持在O(log2n),大大降低了操作的时间复杂度。
平衡二叉树是二叉排序树的另一种形式。
我们希望由任何初始序列构成的二叉排序树都是平衡二叉树。因为平衡二叉树上任何结点的左右子树的深度之差都不超过1,则可以证明它的深度和logN是同数量级的(其中N是结点的个数)。由此,它的平均查找长度也和logN同数量级。
C语言描述:
typedef struct BSTNode {
ElemType data;
int bf; //结点的平衡因子
struct BSTNode *lchild, *rchild;
//左、右孩子指针
} BSTNode, * BSTree;
构造二叉平衡(查找)树的方法是:在插入过程中,采用平衡旋转技术。
插入算法 :
算法思想:
在平衡二叉排序树BBST上插入一个新的数据元素e的递归算法可描述如下:
1.若BBST为空树,则插入一个数据元素为e的新结点作为BBST的根结 点,树的深度增1;
2.若e的关键字和BBST的根结点的关键字相等,则不进行插入;
3.若e的关键字小于BBST的根结点的关键字,而且在BBST的左子树中不存在和e有相同关键字的结点,则将e插入在BBST的左子树上,并且当插入之后的左子树深度增加(+1)时,分别就下列不同情况处理之:
i.BBST的根结点的平衡因子为-1(右子树的深度大于左子树的深度):则将根结点的平衡因子更改为0,BBST的深度不变;
ii.BBST的根结点的平衡因子为0(左、右子树的深度相等):则将根结点的平衡因子更改为1,BBST的深度增1;
iii.BBST的根结点的平衡因子为1(左子树的深度大于右子树的深度):
a. 若BBST的左子树根结点的平衡因子为1,则需进行单向右旋平衡处理,并且在右旋处理之后,将根结点和其右子树根结点的平衡因子更改为0,树的深度不变;
b. 若BBST的左子树根结点的平衡因子为-1,则需进行先向左、后向右的双向旋转平衡处理,并且在旋转处理之后,修改根结点和其左、右子树根结点的平衡因子,树的 深度不变。
4.若e的关键字大于BBST的根结点的关键字,而且在BBST的右子树中不存在和e有相同关键字的结点,则将e插入在BBST的右子树上,并且当插入之后的右子树深度增加(+1)时,分别就不同情况处理之。其处理操作和上述3.中描述相对称。
3. 判定树(决策树):
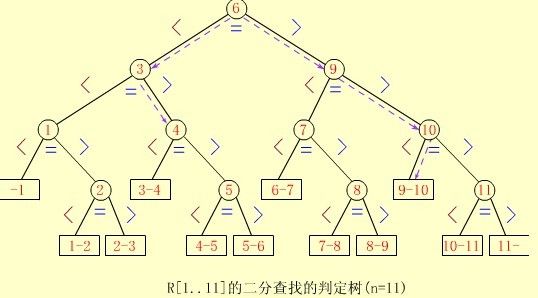
二分查找过程可用二叉树来描述:把当前查找区间的中间位置上的结点作为根,左子表和右子表中的结点分别作为根的左子树和右子树。由此得到的二叉树,称为描述二分查找的判定树(Decision Tree 决策树)或比较树(Comparison Tree)。
判定树的形态只与表结点个数n相关,而与输入实例中R[1..n].keys的取值无关。
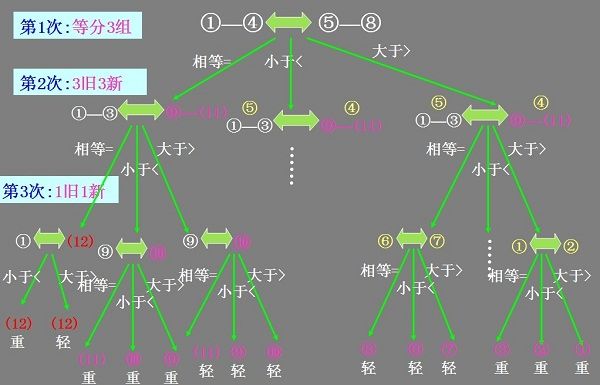
举例:12个球如何用天平只称3次便分出轻重?
分析:12个球中必有一个非轻即重,即共有24种“次品”的可能性。每次天平称重的结果有3种,连称3次应该得到的结果有33=27种。说明仅用3次就能找出次品的可能性是存在的。
思路:首先,将12个球分三组,每组4个,任意取两组称。会有两种情况:平衡,或不平衡。其次,一定要利用已经称过的那些结论;即充分利用“旧球”的标准性作为参考。
【例】对于有11个结点的表,若查找的结点是表中第6个结点,则只需进行一次比较;若查找的结点是表中第3或第9个结点,则需进行二次比较;找第1,4,7,10个结点需要比较三次;找到第2,5,8,11个结点需要比较四次。
由此可见,成功的二分查找过程恰好是走了一条从判定树的根到被查结点的路径,经历比较的关键字次数恰为该结点在树中的层数。若查找失败,则其比较过程是经历了一条从判定树根到某个外部结点的路径,所需的关键字比较次数是该路径上内部结点的总数。
【例】待查表的关键字序列为:(05,13,19,21,37,56,64,75,80,88,92),若要查找K=85的记录,所经过的内部结点为6、9、10,最后到达方形结点"9-10",其比较次数为3。
实际上方形结点中"i-i+1"的含意为被查找值K是介于R[i].key和R[i+1].key之间的,即R[i].key<K<R[i+1].key。
设内部结点的总数为n=2h-1,则判定树是深度为h=lg(n+1)的满二叉树(深度h不计外部结点)。树中第k层上的结点个数为2k-1,查找它们所需的比较次数是k。因此在等概率假设下,二分查找成功时的平均查找长度为:
ASLbn≈lg(n+1)-1
二分查找在查找失败时所需比较的关键字个数不超过判定树的深度,在最坏情况下查找成功的比较次数也不超过判定树的深度。即为:
二分查找的最坏性能和平均性能相当接近。
二分查找的优点和缺点
虽然二分查找的效率高,但是要将表按关键字排序。而排序本身是一种很费时的运算。既使采用高效率的排序方法也要花费O(nlgn)的时间。
二分查找只适用顺序存储结构。为保持表的有序性,在顺序结构里插入和删除都必须移动大量的结点。因此,二分查找特别适用于那种一经建立就很少改动、而又经常需要查找的线性表。
对那些查找少而又经常需要改动的线性表,可采用链表作存储结构,进行顺序查找。链表上无法实现二分查找。
5. 带权树:
即路径带有权值。例如:
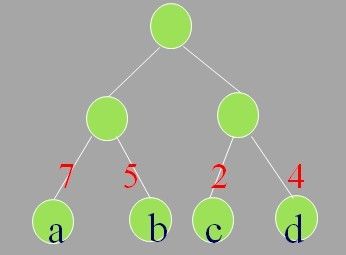
6. 最优树(赫夫曼树):
// stdafx.h : include file for standard system include files,
// or project specific include files that are used frequently, but
// are changed infrequently
//
#pragma once
#include <stdio.h>
#include "stdlib.h"
#include <iostream>
using namespace std;
//宏定义
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
#define STACKEMPTY -3
#define QUEUEEMPTY -3
#define MAX 10 // MAXIMUM STACK CONTENT
#define MAX_QUEUE 10 // MAXIMUM QUEUE CONTENT
typedef int Status;
typedef int ElemType;
typedef struct{
unsigned int weight;
unsigned int parent, lchild,rchild;
}HTNode, *HuffmanTree; //动态分配数组存储赫夫曼树
typedef char * * HuffmanCode;//动态分配数组存储赫夫曼编码表test.cpp文件:
// Test.cpp : Defines the entry point for the console application.
//
#include "stdafx.h"
/************************************************************************/
/* 算法:
*/
/************************************************************************/
void select(HuffmanTree &HT,int n,int &h1,int &h2)
{
int i ,j;
for(i=1;i<=n;i++)
if(!HT[i].parent) //一旦找到父结点不为0的结点就停止
{
h1=i;
break;
}
for(j=i+1;j<=n;j++)
if(!HT[j].parent)
{
h2=j;
break;
}
for(i=1;i<=n;i++)
if(HT[h1].weight>HT[i].weight&&!HT[i].parent&&(h2!=i))
h1=i; //进行比较,找权值最小,和h2不同的结点
for(j=1;j<=n;j++)
if(HT[h2].weight>HT[j].weight&&!HT[j].parent&&(h1!=j))
h2=j; //进行比较,找权值最小,和h1不同的结点
if(h1>h2)
{
int temp; //将权值最小的结点赋给h1
temp=h1;
h1=h2;
h2=temp;
}
}
/************************************************************************/
/*
w存放n 个字符的权值(均>0),构造赫夫曼树HT,并求出n 个字符的赫夫曼编码HC。
*/
/************************************************************************/
void HuffmanCoding(HuffmanTree &HT, HuffmanCode &HC, int *w,int n)
{
if(n<=1) return;
int m,i;
char *cd;
int s1, s2;
// HuffmanTree p;
m = 2*n-1;
HT=(HuffmanTree)malloc((m+1)*sizeof(HTNode)); //0号单元未用
for (i=1; i<=n; i++) { //初始化,相当: p = HT; p = {*w, 0, 0,0 }, ++p;
HT[i].weight=w[i-1];
HT[i].parent=0;
HT[i].lchild=0;
HT[i].rchild=0;
}
for (i=n+1; i<=m; i++) { //初始化 p = {*w, 0, 0,0 }, ++p;
HT[i].weight=0;
HT[i].parent=0;
HT[i].lchild=0;
HT[i].rchild=0;
}
//添加查看便于调试
printf("\n-------------------------------------------");
printf("\n哈夫曼树的构造过程如下所示:\n");
printf("HT初态:\n");
printf(" 结点 weight parent lchild rchild");
for (i=1; i<=m; i++)
printf("\n%4d%8d%8d%8d%8d",i,HT[i].weight,HT[i].parent,HT[i].lchild, HT[i].rchild);
for (i=n+1; i<=m; i++) { // 建哈夫曼树
// 在HT[1..i-1]中选择parent为0且weight最小的两个结点,
// 其序号分别为s1和s2。
select(HT, i-1,s1,s2);
HT[s1].parent = i; HT[s2].parent = i;
HT[i].lchild = s1; HT[i].rchild = s2;
HT[i].weight = HT[s1].weight + HT[s2].weight;
//添加查看,便于调试
printf("\nselect: s1=%d s2=%d\n", s1, s2);
printf(" 结点 weight parent lchild rchild");
for (int j=1; j<=i; j++)
printf("\n%4d%8d%8d%8d%8d",j,HT[j].weight,
HT[j].parent,HT[j].lchild, HT[j].rchild);
}
//---从叶子到根逆向求每个字符的赫夫曼编码---
int start,f;
unsigned int c;
HC=(HuffmanCode)malloc((n+1)*sizeof(char *)); //分配n个字符编码的头指针向量
cd=(char *)malloc(n*sizeof(char)); //分配求编码的工作空间
cd[n-1]='\0'; //编码结束符
for(i=1;i<=n;++i)
{
//逐个字符求赫夫曼编码
start=n-1;
for(c=i,f=HT[i].parent;f!=0;c=f,f=HT[f].parent)//从叶子到根逆向求编码
if(HT[f].lchild==c)
cd[--start]='0';
else
cd[--start]='1';
HC[i]=(char *)malloc((n-start)*sizeof(char)); //为第i个字符编码分配空间
strcpy(HC[i],&cd[start]); //从cd复制编码到HC
}
free(cd); //释放工作区间
}
void main()
{
HuffmanTree HT; HuffmanCode HC; int *w,n,i;
printf("输入结点数: ");
scanf("%d",&n);
HC=(HuffmanCode)malloc(n*sizeof(HuffmanCode));
w=(int *)malloc(n*sizeof(int));
printf("输入%d个结点的权值: ",n);
for(i=0;i<n;i++)
scanf("%d",&w[i]);
HuffmanCoding(HT,HC,w,n);
printf("\n-------------------------------------------\n");
printf("\n各结点的赫夫曼编码:\n");
printf("编号 权值 编码\n");
for(i=1;i<=n;i++)
printf("%2d,%6d:%6s\n",i,w[i-1],HC[i]);
}