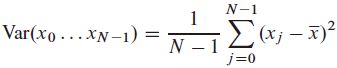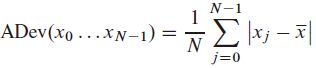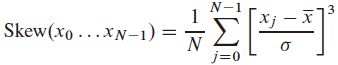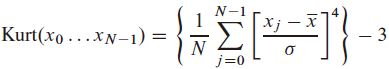[摘记]数值方法10——数据的统计描述

注：以下来自《C++数值算法一书》，仅对章节内容做摘要，为的是给自己扫盲，不涉及算法。

第12章与第13章讲傅里叶变换的，由于时间关系，我暂时没有看这几章，与项目关系不大（而且我信号与线性系统学的很糟糕，各种混乱）。

数据的统计描述主要讲述一些概率论与数理统计的基本知识。

1. 分布的矩：均值、方差、偏斜度等

当一组数据有很强的集中趋势，即某一特殊值周围聚集的趋势，则用与矩有关的一些量来表征这组数。矩为这些量的整数幂之和。

最常见的是均值：

均值依赖于数据的一阶矩，而接下来介绍的方差和标准差，依赖于二阶矩：

实际生活中，有时会遇到二阶矩并不存在（无穷大）的分布，这是需要一个更稳健的估算量是平均偏差或平均绝对偏差：

较高的矩或涉及输入数据较高幂次的统计量，在稳健性上总是低于较低矩或仅涉及线性和或计算的统计量，因此，三阶矩 偏斜度 和四阶矩 峭度应当谨慎使用。

 

2. 两种分布是否具有相同的均值和方差

测量均值之差显著性的量并不是区分它们的标准差之值，而是区分它们的标准误之值。

针对显著不同均值的常用测量统计量称为学生t，针对显著不同方差的方法是F检验。

 

3. 两种分布是否不同

这是比均值方差的问题更一般化的问题，对于离散分布之间的差异，可以接受的检验是χ²检验，对于单变量函数的连续数据组，最常用的检验是Kolmogorov-Smirnov检验。

 

4. 两种分布的列联表分析

一个变量，当它的值是某一无序集合的成员时，称其为公称的，如省份名字。当一变量的值是某一离散而有序集合的元素时，则称该变量是有序的，如学校的年级。而如果它的值是实数，我们称之为连续的，如时间，温度。

对于任何一对公称变量，数据能用一列联表来显示，公称变量之间的关联的分析称为列联表分析或交叉列表分析，主要介绍两种方法。

基于χ²统计量的方法，能较好地表征这种关联的显著性，但它用作强度的测度却很一般；第二种方法是基于信息论中熵的概念，它没有引入关联显著性，但能非常明确地表征已知很显著的关联强度。

 

5. 线性相关

顺序量或连续量的测度最常用的是线性相关系数。但它的显著性解释具有不确定性，导致了非参数相关或秩相关这样的概念。非参数相关比线性相关更稳健，也更宜于消除数据中未知的缺陷。书上讨论两个统计量，Spearman秩阶相关系数r_s和Kendall的τ。

 

本文原创，转载请注明出处

http://www.cnblogs.com/luluathena/