民办生从零学C的第十一天：操作符

每日励志：我们可以随时的转身，但是决不能后退。

一.操作符的分类

• 算术操作符：+、-、*、/、%

• 移位操作符：<<、>>

• 位操作符：&、|、^

• 赋值操作符：=、+=、-=、*=、/=、%=、<<=、>>=、&=、|=、^=

• 单目操作符：!、++、--、&、*、+、-、~、sizeof、(类型)

• 关系操作符：>、>=、<、<=、==、!=

• 逻辑操作符：&&、||

• 条件操作符：?:

• 逗号表达式：,

• 下标引用：[]

• 函数调用：()

• 结构成员访问：.、->

二.二进制与进制转换

1.二进制

二进制是计算机中数据存储和运算的基础，它只有两个数字：0 和 1。二进制的每一位代表一个幂次的 2。

eg 二进制数1011可以表示为：

1×2³ + 0×2² + 1×2¹ + 1×2⁰ = 8 + 0 + 2 + 1 = 11

2.进制转换

a. 十进制转二进制

将十进制数转换为二进制数，可以采用“除以 2 取余法”。具体步骤如下：

1. 将十进制数除以 2，得到商和余数。

2. 将商继续除以 2，直到商为 0。

3. 将每次得到的余数倒序排列，即为二进制数。

示例：将十进制数 11 转换为二进制。

11 ÷ 2 = 5 余 1
5 ÷ 2 = 2 余 1
2 ÷ 2 = 1 余 0
1 ÷ 2 = 0 余 1

所以余数倒序排列可得：1011

b.二进制转八进制

8进制的数字每一位是0~7的，0~7的数字，各自写成2进制，最多有3个2进制位就足够了。

从右到左将二进制数每3位分为一组，不足3位的在前面补0，然后将每组二进制数转换为对应的八进制数。

八进制表示的时候在前面加 0

eg 将二进制数10110101转换为八进制。

1. 分组：从右到左每3位分为一组。

   10110101 → 10 110 101

   • 第一组：101（右边第一组，3位）

   • 第二组：110（中间一组，3位）

   • 第三组：10（左边最后一组，不足3位，在前面补0 → 010）

2. 转换每组：

   • 010 → 2（因为 0×2² + 1×2¹ + 0×2⁰ = 0 + 2 + 0 = 2）

   • 110 → 6（因为 1×2² + 1×2¹ + 0×2⁰ = 4 + 2 + 0 = 6）

   • 101 → 5（因为 1×2² + 0×2¹ + 1×2⁰ = 4 + 0 + 1 = 5）

3. 组合结果：0265

c.二进制转十六进制

16进制的数字每一位是0~9，a~f 的，0~9 , a~f 的数字，各自写成2进制，最多有4个2进制位就足够了，

从右到左将二进制数每4位分为一组，不足4位的在前面补0。 将每组二进制数转换为对应的十六进制数。

16进制表示的时候前面加0x

十进制数字      1  2  3  4  5  6  7  8  9  10  11   12  13  14  15  16

十六进制数字  1  2  3  4  5  6  7  8  9   a     b     c    d    e    f    g

eg 将二进制数10110101转换为十六进制。

1. 分组：从右到左每4位分为一组。

   10110101 → 1011 0101

2. 转换每组：

   • 1011 → B（因为 11 = 8 + 2 + 1 = 1×2³ + 0×2² + 1×2¹ + 1×2⁰）

   • 0101 → 5（因为 5 = 4 + 1 = 0×2³ + 1×2² + 0×2¹ + 1×2⁰）

3. 组合结果：0xB5

三.原码 反码 补码 

它们是整数二进制的表示方法，高位是符号位，其余位表示数值。

正数：符号位为0，其余位为数值的二进制表示。 负数：符号位为1，其余位为数值的二进制表示。

1.原码

直接将数值按照正负数的形式翻译成二进制得到的就是原码。

eg

• 二进制数0101（即十进制的5）的32位原码是：

  00000000000000000000000000000101

• 二进制数1101（即十进制的-5）的32位原码是：

  10000000000000000000000000000101

2.反码

将原码的符号位不变，其他位依次按位取反就可以得到反码，它是对原码的改进，用于简化减法运算。

正数的反码等于它的原码，反码实际上是为负数服务的

eg

• 二进制数0101（即十进制的5）的32位反码是：

  00000000000000000000000000000101

• 二进制数1101（即十进制的-5）的32位原码是：

  10000000000000000000000000000101

  其反码是：

  11111111111111111111111111111010

3.补码

反码（二进制）+1就得到补码，主要用于简化加减法运算，并且解决了原码和反码中存在的+0和-0的问题。

正数的补码等于它的原码，补码也是为负数服务的

整数在内存中存储的是2进制的补码

在原码和反码的表示方法中，存在两个不同的表示形式来表示零，即正零（+0）和负零（-0）。这可能会导致一些混淆和问题，因为正零和负零在数值上是相等的，但在表示上却不同。补码解决了这个问题，使得零只有一个表示形式

原码和反码中的+0和-0（用八位二进制进行解释）

• 原码中的零：

  • 正零：00000000

  • 负零：10000000

• 反码中的零：

  • 正零：00000000

  • 负零：11111111

在原码和反码中，正零和负零是不同的表示形式，这可能会导致一些问题，比如在比较两个数是否相等时需要额外的处理。但在补码表示中，零只有一个表示形式，即 00000000。这是因为补码的定义消除了正零和负零的区别。

按照补码的定义，负零的补码应该是反码加1。负零的原码是10000000，反码是11111111，反码加1后得到00000000（因为11111111 + 1 = 100000000，但（如果最高位有进位，则溢出位被丢弃）溢出的位被丢弃。

因此，在补码表示中，正零和负零都表示为00000000，从而消除了+0和-0的问题。

eg

• 二进制数0101（即十进制的5）的32位补码是：

  00000000000000000000000000000101

• 二进制数1101（即十进制的-5）的32位原码是：

  10000000000000000000000000000101

  其反码是：

  11111111111111111111111111111010

  补码是：

  11111111111111111111111111111011

4.转换

• 原码转反码：正数不变，负数的数值位取反。

• 反码转补码：正数不变，负数的反码加1。

• 补码转原码：正数不变，负数的补码减1得到反码，再取反得到原码。

正数5

• 原码：00000000000000000000000000000101

• 反码：00000000000000000000000000000101

• 补码：00000000000000000000000000000101

负数-5

• 原码：10000000000000000000000000000101

• 反码：11111111111111111111111111111010

• 补码：11111111111111111111111111111011

5.计算

a.原码与原码的计算

需要单独处理符号位，符号位不会直接参与数值的加法运算，也不会因为数值位的进位而改变。

同号相加：

两个正数相加（符号位为0）：直接相加，结果为正。

两个负数相加（符号位为1）：直接相加，结果为负。

异号相加：

正数加负数（符号位由绝对值较大的数的符号决定）：比较绝对值大小，绝对值大的数决定结果的符号。

eg

• 5的原码：00000000 00000000 00000000 00000101

• 3的原码：00000000 00000000 00000000 00000011

• 结果是  ：00000000 00000000 00000000   00001000

• -5的原码：10000000 00000000 00000000 00000101

• -3的原码：10000000 00000000 00000000 00000011

•  结果是      10000000 00000000 00000000 00000110  原码表示的-8​​​

• 5的原码： 00000000 00000000 00000000 00000101

• -3的原码：10000000 00000000 00000000 00000011

• 结果是       00000000 00000000 00000000 00000010

b.补码与补码的计算

可以直接进行加减法运算，无需处理符号位，运算简单且高效。

• 5的补码：  00000000 00000000 00000000 00000101

• -3的补码： 11111111 11111111 11111111 11111101

• 结果是        00000000 00000000 00000000 00000010 最高位的进位被丢弃

四.移位操作符

移动的是二进制数

1.左移操作符（<<）     

• 功能：将一个二进制数向左移动指定的位数。

• 数学意义：左移`n`位相当于将该数乘以 (2^n)。

• 原理：左移操作会在右侧补0，左侧溢出的位会被丢弃。

eg
 5 << 1：二进制 0101 左移1位变为 1010，即十进制的 10
 3 << 2：二进制 0011 左移2位变为 1100，即十进制的 12

2.右移操作符（>>） 

• 功能：将一个二进制数向右移动指定的位数。

• 数学意义：右移`n`位相当于将该数除以(2^n)（取整）。

• 原理：右移操作会丢弃右侧的位，左侧的空位用符号位填充（对于有符号数）或用0填充（对于无符号数）。

eg

8 >> 1：二进制 1000 右移1位变为 0100，即十进制的 4

10 >> 2：二进制 1010 右移2位变为 0010，即十进制的 2

移位规则:首先右移运算分两种:
1.逻辑右移:左边用0填充，右边丢弃
2.算术右移:左边用原该值的符号位填充，右边丢弃

右移到底采用算术右移还是逻辑右移是取决于编译器的，通常采用的都是算术右移

对于移位运算符，不要移动负数位，这个是标准未定义的。

五.位操作符 （& | ^ ~）

作用于补码表示的数值

1. 按位与（&）

两个操作数的每一位进行与运算。只有当两个位都为1时，结果才为1，否则为0

（同1则1，有0为0） 常用于清零

int a = 5;    
// 32位补码：00000000 00000000 00000000 00000101
int b = 3;    
// 32位补码：00000000 00000000 00000000 00000011

int result = a & b;
// 结果：    00000000 00000000 00000000 00000001 
//           1

补充： n = n & (n-1) 是一个常见的位运算技巧，用于清除整数 n 二进制表示中最右边的 1。

计算过程：

     110 (6)
&  101 (5)
     ------
     100 (4)

常用于统计二进制中 1 的个数或检查是否为 2 的幂次。

//统计二进制中 1 的个数

int countOnes(int n) 
{
    int count = 0;
    while (n != 0) {
        count++;
        n = n & (n - 1); // 清除最右边的1
    }
    return count;
}

//检查是否为 2 的幂次

int isPowerOfTwo(int n) {
    return n != 0 && (n & (n - 1)) == 0;
}

2. 按位或（|）

两个操作数的每一位进行或运算。只要有一个位为1，结果就为1，否则为0。

（有1则1，无1则0）常用于将指定位设置为1

int a = 5;    
// 32位补码：00000000 00000000 00000000 00000101
int b = 3;    
// 32位补码：00000000 00000000 00000000 00000011

int result = a | b;
//     结果：00000000 00000000 00000000 00000111 

//        7

3. 按位异或（^）

两个操作数的每一位进行异或运算。只有当两个位不同时，结果才为1，否则为0。

（相异为1，相同为0）

int a = 5;    
// 32位补码：00000000 00000000 00000000 00000101
int b = 3;   
// 32位补码：00000000 00000000 00000000 00000011

int result = a ^ b;
// 结果：    00000000 00000000 00000000 00000110 
//         6

4. 按位取反（~）

对一个操作数的每一位取反。0变成1，1变成0。

int a = 5;    
// 32位补码：00000000 00000000 00000000 00000101

int result = ~a;
// 结果：    11111111 11111111 11111111 11111010 
//       -6

注意，&，| 要与&&，||区别开，

前者关注二进制的计算，后者关注逻辑的真假

一道变态的面试题:
不能创建临时变量(第三个变量)，实现两个整数的交换。

如果是可以创建变量的话，那很简单

#include 
int main()
{
   int a = 5;
   int b = 2;
   int c = 0;

   c = a;
   a = b;
   b = c;

  printf("a = %d\n",a);
  printf("b = %d\n",b);

    return 0;
}

但是题目要求不能创建变量，所以我们就必须从其他方向下手

1）.加减法

#include 
int main()
{
   int a = 5;
   int b = 2;

   a = a + b; 
   b = a - b;
   a = a - b;

  printf("a = %d\n",a);
  printf("b = %d\n",b);

    return 0;
}

2）.使用异或法交换

补充：

异或运算基础

异或运算是一种位运算，符号为 ^ 。它的规则如下：

• 0 ^ 0 = 0

• 0 ^ 1 = 1

• 1 ^ 0 = 1

• 1 ^ 1 = 0

异或运算的两个重要性质：

1. 一个数与自身异或结果为0：a ^ a = 0

2. 一个数与0异或结果不变：a ^ 0 = a

#include 
int main()
{

    int a = 5;
    int b = 2;

    a = a ^ b;
    b = a ^ b;
    a = a ^ b;

    printf("a = %d\n",a);
    printf("b = %d\n",b);

    return 0 ;
}

一共有三种方法可以解决交换变量的问题，但在外面实际编程中，我们还是使用第一种创建变量的方法，因为它的可读性高，易理解。

六.单目操作符

1. 自增自减操作符

  ++

  -- 

2. 取地址操作符（&）

用于获取变量的内存地址。

3. 间接访问操作符（*）

用于访问指针变量所指向的内存地址中的值。

4. 正负号操作符（+ 和 -）

用于对数值进行正负号的转换。

5. 逻辑非操作符（！）

用于对布尔值取反。

6. 求大小操作符（sizeof ）

用于计算数据类型或变量所占的字节数。

7. 按位非操作符（~）

用于对数值的二进制表示取反（按位取反）。

七.逗号表达式

它使用逗号操作符（ , ）将多个表达式连接在一起，从左向右依次执行，整个表达式的结果是最后一个表达式的结果。

其基本形式为：表达式 1, 表达式 2, 表达式 3,..., 表达式 n。

//使用逗号表达式
#include 

int main() 
{
    int a = 5, b = 10;
    printf("Sum: %d, Product: %d\n", a + b, a * b);
    return 0;
}

//不使用逗号表达式
#include 

int main() 
{
    int a = 5;
    int b = 10;
    int sum = a + b;
    int product = a * b;
    printf("Sum: %d, Product: %d\n", sum, product);
    return 0;
}

八.下标访问 [ ] 、函数调用 ( ) 

1.下标访问操作符 [ ]

• 下标访问操作符[]用于访问数组中的元素，其语法为  数组名  [索引]。

• 索引从0开始，表示元素在数组中的位置。

对于数组int arr[5] = {1, 2, 3, 4, 5};：

• arr[0]访问数组的第一个元素，值为1。

• arr[2]访问数组的第三个元素，值为3。

 操作数:一个数组名 +一个索引值(下标)

2.函数调用操作符 ( )

• 函数调用操作符()用于调用一个函数，其语法为  函数名(参数列表)。

• 参数列表是传递给函数的值，用于函数内部的处理。

#include 

int add(int a, int b) 
{
    return a + b;
}

int main() 
{
    int result = add(3, 5);
    printf("Result: %d\n", result);
    return 0;
}

操作数:第一个操作数是函数名，剩余的操作数就是传递给函数的参数。

九.结构成员访问操作符

C语言提供了多种内置类型供我们使用，例如 int，char，double等，但这些是不够用的，就例如我想描述一个学生，他的名字，他的年龄，他的性别，他的成绩等等，这个时候单一的内置类型就无法满足我们的使用。所以，C语言为了解决这个问题增加了结构体这种自定义的数据类型，让我们可以自己创造适合的类型。

1.结构体定义

使用struct关键字定义一个结构体

struct 结构体名 
{
    成员类型1 成员名1;
    成员类型2 成员名2;
    ...
    成员类型n 成员名n;

}变量列表= { 初始化值列表 };

2.例子

#include 

// 方式1：先定义结构体，再声明变量
struct Person 
{
    char name[50];
    int age;
};

int main() 
{
    struct Person p1;
    // 赋值和使用p1...

    // 方式2：在定义结构体的同时声明变量
    struct Student {
        char name[50];
        int id;
    } s1, s2; 
      // 声明了两个Student类型的变量s1和s2

    return 0;
}

#include 

// 定义一个结构体Point，包含两个int成员x和y
struct Point
{
    int x;
    int y;

};

// 定义一个结构体Student，包含char数组name、int成员age和double成员score

struct Student
{
    char name[20];
    int age;
    double score;
};

// 定义一个结构体S，包含char成员ch、struct Point成员p、int数组arr和double成员d
struct S
{
    char ch;
    struct Point p;
    int arr[10];
    double d;

};

int main()
{
    // 声明并初始化struct Student类型的变量s1和s2
    struct Student s1 = { "牢大",24,24.8};
    struct Student s2 = { "孙笑川",42,44.8 };

    // 声明并初始化struct Point类型的变量p
    struct Point p = { 24,8 };
    // 声明并初始化struct S类型的变量s
    struct S s = { 'z',{2,4},{1,2,3,4,5,6,7,8,9,10},3.14159 };


    // 打印struct S变量s的成员ch
    printf("%c\n", s.ch);
    // 打印struct S变量s的成员p的x和y
    printf("%d %d\n", s.p.x, s.p.y);
    // 打印struct Student变量s1和s2的成员
    printf("学生1: %s, 年龄:%d, 成绩:%.2f\n", s1.name, s1.age, s1.score);
    printf("学生2: %s, 年龄:%d, 成绩:%.2f\n", s2.name, s2.age, s2.score);

    // 打印struct Point变量p的成员
    printf("点坐标: (%d, %d)\n", p.x, p.y);

    return 0;
}

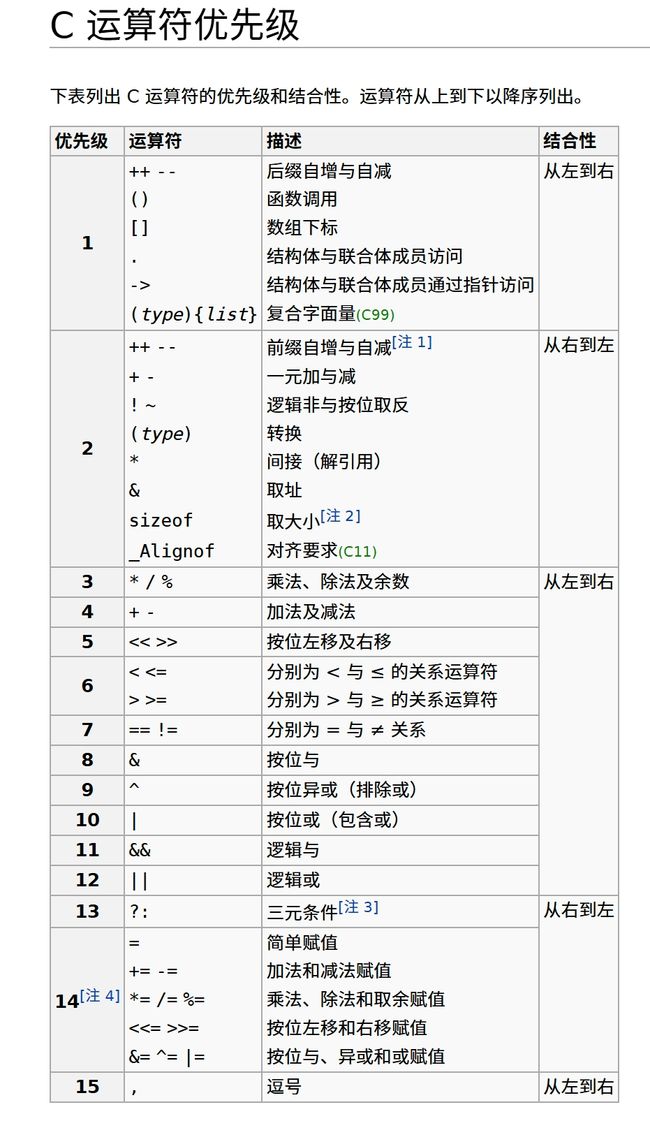
十.操作符的属性:  优先级、结合性

1.优先级

• 操作符的优先级决定了在没有括号的情况下，哪个操作会先执行。优先级高的操作符会先于优先级低的操作符执行。

• 例如，在表达式 3 + 4 * 5 中，* 的优先级高于 +，所以先计算 4 * 5，结果是 20，然后再与 3 相加得到 23。

2.结合性

• 结合性决定了同优先级的操作符在表达式中如何分组。它有两种方向：左结合和右结合。

• 左结合性表示同优先级的操作符从左到右依次执行。例如，表达式 a - b - c 中，- 是左结合的，先计算 a - b，再用结果减去 c。

• 右结合性表示同优先级的操作符从右到左依次执行。例如，赋值操作符 = 是右结合的，表达式 a = b = c 中，先执行 b = c，再将结果赋给 a。

• C 运算符优先级 - cppreference.com