Social Network Analysis

Week1 : Introduction

1A Why Social Network Analysis?

What are networks?  Networks are sets of nodes connected by edges

goal: characterize network structure

¤  Are nodes connected through the network? (week )1

¤   How far apart are they? (week 1)

¤   Are some nodes more important due to their position in the network? (week 3)

¤   Is the network composed of communities? (week 4)

goal: model network formation

¤  Randomly generated networks (week 2)

¤   Preferential attachment (week 2)

¤   Small-world networks (week 5)

¤   Optimization, strategic network formation (week 5)

goal: understand how network structure affects processes

¤  information diffusion (weeks 2 & 6)

¤   opinion formation (week 6)

¤   coordination/cooperation (week 6)

¤   resilience to attack (week 2)

What about weeks 7 & 8?

¤  Week 7: cool and unusual applications of SNA

¤   Week 8: SNA and online social networks

 

1B Software Tools

¤   Gephi (visualization and basic network metrics) 

¤   NetLogo (modeling network dynamics)

¤   iGraph (for programming assignments)

 

use Gephi

¤  Download from: http://gephi.org/

¤  download the datafile dining.gephi from Coursera

¤  let’s play

 

Gephi:

         Context: node, edge

         Edit: see node property

         Layout: change layout

         Change color of nodes

         Change size of nodes

         Partition-edges-labels:

Preview:

 

1C Degree and Connected Component

Edge: directed, undirected

 

Data representation:

Adjacency matrix

Edge list

Adjacency list

 

Strongly connected component

Weakly connected component

 

Giant component: as the network gets infinitely large, the giant component is still going to occupy a finite fraction of it.

 

 

1D Gephi Demo

 

Gephi:

Ranking-nodes-indegree: change node size according to their indegree.  Spline:

Statistics:  calculate Average Degree

Statistics:  Connected Component

Partition: partition the nodes by strongly connected component

 

 

HW 1: a Facebook network

http://snacourse.com/getnet  

NetGet 用来获取facebook用户关系网

Week2 : Random Graph Models

2P intro remarks for week2

Project: peer graded

 

 

2A introduction to random graph models

 

Erdös-Renyi: simplest network model

 

Degree distribution

¤  (N,p)-model: For each potential edge we flip a biased coin

¤  with probability p we add the edge

¤  with probability (1-p) we don’t

 

 

 

use NetLogo

 

 

How many edges per node?

¤  Each node has (N – 1) tries to get edges

¤   Each try is a success with probability p

¤   The binomial distribution gives us the probability that a node has degree k:

 

 

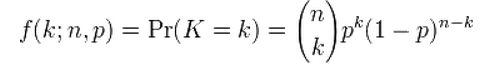
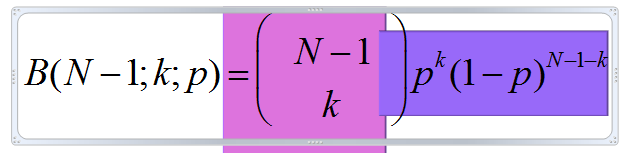
一个node有k个edge的可能性B(N-1,k,p)

 

What is the mean?

¤  Average degree z =  (n-1)*p

 

 

 

Week3 : Centrality

3A degree, betweenness, closeness

 

 

http://moviegalaxies.com/

电影人物关系图

 

different notions of centrality

         indegree

         outdegree

         betweenness

         closeness

 

 

normalization

 

Brokerage

 

betweenness: capturing brokerage

 

 

Some people have high betweenness but low degree,

Some people have high degree but low betweenness.

 

 

closeness