基于爬山算法求解TSP问题(JAVA)
一、TSP问题
TSP问题(Travelling Salesman Problem)即旅行商问题,又译为旅行推销员问题、货郎担问题,是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
TSP问题是一个组合优化问题。该问题可以被证明具有NPC计算复杂性。TSP问题可以分为两类,一类是对称TSP问题(Symmetric TSP),另一类是非对称问题(Asymmetric TSP)。所有的TSP问题都可以用一个图(Graph)来描述:
V={c1, c2, …, ci, …, cn},i = 1,2, …, n,是所有城市的集合. ci表示第i个城市, n为城市的数目;
E={(r, s): r,s∈ V}是所有城市之间连接的集合;
C = {crs: r,s∈ V}是所有城市之间连接的成本度量(一般为城市之间的距离);
如果crs = csr, 那么该TSP问题为对称的,否则为非对称的。
一个TSP问题可以表达为:
求解遍历图G = (V, E, C),所有的节点一次并且回到起始节点,使得连接这些节点的路径成本最低。
二、爬山算法
爬山算法是一种局部择优的方法,采用启发式方法,是对深度优先搜索的一种改进,它利用反馈信息帮助生成解的决策。 该算法每次从当前解的临近解空间中选择一个最优解作为当前解,直到达到一个局部最优解。属于人工智能算法的一种。
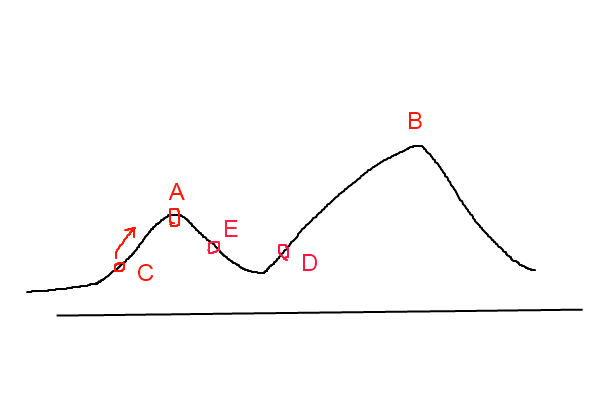
爬山算法实现很简单,其主要缺点是会陷入局部最优解,而不一定能搜索到全局最优解。如下图所示:假设C点为当前解,爬山算法搜索到A点这个局部最优解就会停止搜索,因为在A点无论向那个方向小幅度移动都不能得到更优的解。
爬山算法实施步骤:
三、爬山算法求解TSP问题
在该JAVA实现中我们选择使用tsplib上的数据att48,这是一个对称TSP问题,城市规模为48,其最优值为10628.其距离计算方法下图所示:
具体代码如下:
package noah;
import java.io.BufferedReader;
import java.io.FileInputStream;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Random;
public class HillClimbing {
private int MAX_GEN;// 迭代次数
private int cityNum; // 城市数量,编码长度
private int[][] distance; // 距离矩阵
private int bestT;// 最佳出现代数
private int[] bestGh;// 最好的路径编码
private int bestEvaluation;
private Random random;
public HillClimbing() {
}
/**
* constructor of GA
*
* @param n
* 城市数量
* @param g
* 运行代数
*
**/
public HillClimbing(int n, int g) {
cityNum = n;
MAX_GEN = g;
}
// 给编译器一条指令,告诉它对被批注的代码元素内部的某些警告保持静默
@SuppressWarnings("resource")
/**
* 初始化HillClimbing算法类
* @param filename 数据文件名,该文件存储所有城市节点坐标数据
* @throws IOException
*/
private void init(String filename) throws IOException {
// 读取数据
int[] x;
int[] y;
String strbuff;
BufferedReader data = new BufferedReader(new InputStreamReader(
new FileInputStream(filename)));
distance = new int[cityNum][cityNum];
x = new int[cityNum];
y = new int[cityNum];
for (int i = 0; i < cityNum; i++) {
// 读取一行数据,数据格式1 6734 1453
strbuff = data.readLine();
// 字符分割
String[] strcol = strbuff.split(" ");
x[i] = Integer.valueOf(strcol[1]);// x坐标
y[i] = Integer.valueOf(strcol[2]);// y坐标
}
// 计算距离矩阵
// 针对具体问题,距离计算方法也不一样,
// 此处用的是att48作为案例,它有48个城市,距离计算方法为伪欧氏距离,最优值为10628
for (int i = 0; i < cityNum - 1; i++) {
distance[i][i] = 0; // 对角线为0
for (int j = i + 1; j < cityNum; j++) {
double rij = Math
.sqrt(((x[i] - x[j]) * (x[i] - x[j]) + (y[i] - y[j])
* (y[i] - y[j])) / 10.0);
// 四舍五入,取整
int tij = (int) Math.round(rij);
if (tij < rij) {
distance[i][j] = tij + 1;
distance[j][i] = distance[i][j];
} else {
distance[i][j] = tij;
distance[j][i] = distance[i][j];
}
}
}
distance[cityNum - 1][cityNum - 1] = 0;
bestGh = new int[cityNum];
bestEvaluation = Integer.MAX_VALUE;
bestT = 0;
random = new Random(System.currentTimeMillis());
}
// 初始化编码Ghh
void initGroup() {
int i, j;
bestGh[0] = random.nextInt(65535) % cityNum;
for (i = 1; i < cityNum;)// 编码长度
{
bestGh[i] = random.nextInt(65535) % cityNum;
for (j = 0; j < i; j++) {
if (bestGh[i] == bestGh[j]) {
break;
}
}
if (j == i) {
i++;
}
}
}
public int evaluate(int[] chr) {
int len = 0;
// 染色体,起始城市,城市1,城市2...城市n
for (int i = 1; i < cityNum; i++) {
len += distance[chr[i - 1]][chr[i]];
}
// 城市n,起始城市
len += distance[chr[cityNum - 1]][chr[0]];
return len;
}
// 爬山算法
public void pashan(int[] Gh, int T) {
int i, temp, tt = 0;
int ran1, ran2;
int e;// 评价新值
int[] tempGh = new int[cityNum];
bestEvaluation = evaluate(Gh);
// 爬山代数T
for (tt = 0; tt < T; tt++) {
for (i = 0; i < cityNum; i++) {
tempGh[i] = Gh[i];
}
ran1 = random.nextInt(65535) % cityNum;
ran2 = random.nextInt(65535) % cityNum;
while (ran1 == ran2) {
ran2 = random.nextInt(65535) % cityNum;
}
// 两交换法实施邻域操作
temp = tempGh[ran1];
tempGh[ran1] = tempGh[ran2];
tempGh[ran2] = temp;
e = evaluate(tempGh);// 评价新值
if (e < bestEvaluation) {
bestT = tt;
bestEvaluation = e;
for (i = 0; i < cityNum; i++) {
Gh[i] = tempGh[i];
}
}
}
}
public void solve() {
initGroup();// 初始化编码
pashan(bestGh, MAX_GEN);
System.out.println("最佳长度出现代数:");
System.out.println(bestT);
System.out.println("最佳长度");
System.out.println(bestEvaluation);
System.out.println("最佳路径:");
for (int i = 0; i < cityNum; i++) {
System.out.print(bestGh[i] + ",");
if (i % 10 == 0 && i != 0) {
System.out.println();
}
}
}
/**
* @param args
* @throws IOException
*/
public static void main(String[] args) throws IOException {
System.out.println("Start....");
HillClimbing hillClimbing = new HillClimbing(48, 5000);
hillClimbing.init("c://data.txt");
hillClimbing.solve();
}
}
运行结果截图:
四、总结
爬山算法由于其简单的结构,在处理多约束大规模问题时比较力不从心,很难得到较好的解,但在小规模的NP问题求解中,解的质量还是比较好的;此外爬山算法结构简单,在某些情况下,整体效率比A星算法的效果还好。
注:本文部分内容来源于网络,但程序以及分析结果属于本人成果,转载请注明!