POJ3083-Children of the Candy Corn
转载请注明出处:優YoU http://user.qzone.qq.com/289065406/blog/1303432339
题目大意:
给定一个迷宫,S是起点,E是终点,#是墙不可走,.可以走
先输出左转优先时,从S到E的步数
再输出右转优先时,从S到E的步数
最后输出S到E的最短步数
W为宽,列数
H为高,行数
解题思路:
DFS和BFS的综合题水题,难度不大,但是写代码时要注意几方面:
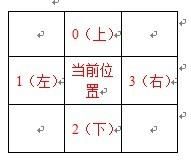
1、 左转、右转优先搜索时必须标记当前位置时的方向,我定义的方向是
最初的方向由起点S确定,而下一步的方向则由前一步的走向决定
例如 左边优先搜索:
当前位置的方向指向 1(向左),(这同时说明前一步是在第“3”的位置走过来的)
那么走下一步时,就要根据2103的顺序,先逐格确定当前位置周边的四格是否可行
若第一次确认2可行,就走到2,在位置2时的方向为2(向下)
若2不可行,则再确定1,若1可行,就走到1,在位置1时的方向为1(向左)
若1也不可行,则再确定0,若0可行,就走到0,在位置0时的方向为0(向上)
若0也不可行,说明进入了迷宫的死胡同,要从原路返回,走回3
右边优先搜索也同理。
根据我定义的方向,设当前位置为d,那么
左转,用数学式子表达就是 d=(d+1)%4
右转,用数学式子表达就是 d=(d+3)%4
我比较懒,在我的程序中,DFS和BFS都用了多入口的做法,有兴趣的同学可以利用我给出的这两个式子对代码进行优化。
这里有一点必须要注意的:
左边、右边优先搜索都不是找最短路,因此走过的路可以再走,无需标记走过的格
2、 寻找最短路只能用BFS
因此在做第3问时别傻乎乎的又用DFS,DFS对于样例的输入确实和BFS得到的结果一样的,别以为样例PASS就提交了。。。所以我就说样例没代表性,学会测试数据很重要= =
注意有一点:
要求E的最短路,必须把迷宫模拟为树,S为根,找到E所在的层(树深),该层就是S到E的最短路,处理技巧就是在BFS时,令queue[tail]的depth等于对应的queue[head]的depth+1,详细见我的程序
把循环的次数作为深度就铁定错的
1 //Memory Time
2 // 212K 0MS
3
4 #include<iostream>
5 using namespace std;
6
7 typedef class
8 {
9 public:
10 int r,c;
11 int depth;
12 }SE;
13
14 SE s,e; //起止点
15 int Lstep; //左边优先搜索 时从S到E的总步数
16 int Rstep; //右边优先搜索 时从S到E的总步数
17 int shortstep; //S到E的最少总步数
18
19 bool maze[41][41]; //记录迷宫的“可行域”与“墙”
20
21 void DFS_LF(int i,int j,int d) //左边优先搜索,i,j为当前点坐标,d为当前位置方向
22 {
23 Lstep++;
24 if(i==e.r && j==e.c)
25 return;
26
27 switch(d)
28 {
29 case 0:
30 {
31 if(maze[i][j-1])
32 DFS_LF(i,j-1,1);
33 else if(maze[i-1][j])
34 DFS_LF(i-1,j,0);
35 else if(maze[i][j+1])
36 DFS_LF(i,j+1,3);
37 else if(maze[i+1][j])
38 DFS_LF(i+1,j,2);
39 break;
40 }
41 case 1:
42 {
43 if(maze[i+1][j])
44 DFS_LF(i+1,j,2);
45 else if(maze[i][j-1])
46 DFS_LF(i,j-1,1);
47 else if(maze[i-1][j])
48 DFS_LF(i-1,j,0);
49 else if(maze[i][j+1])
50 DFS_LF(i,j+1,3);
51 break;
52 }
53 case 2:
54 {
55 if(maze[i][j+1])
56 DFS_LF(i,j+1,3);
57 else if(maze[i+1][j])
58 DFS_LF(i+1,j,2);
59 else if(maze[i][j-1])
60 DFS_LF(i,j-1,1);
61 else if(maze[i-1][j])
62 DFS_LF(i-1,j,0);
63 break;
64 }
65 case 3:
66 {
67 if(maze[i-1][j])
68 DFS_LF(i-1,j,0);
69 else if(maze[i][j+1])
70 DFS_LF(i,j+1,3);
71 else if(maze[i+1][j])
72 DFS_LF(i+1,j,2);
73 else if(maze[i][j-1])
74 DFS_LF(i,j-1,1);
75 break;
76 }
77 }
78
79 return;
80 }
81
82 void DFS_RF(int i,int j,int d) //右边优先搜索,i,j为当前点坐标,d为当前位置方向
83 {
84 Rstep++;
85 if(i==e.r && j==e.c)
86 return;
87
88 switch(d)
89 {
90 case 0:
91 {
92 if(maze[i][j+1])
93 DFS_RF(i,j+1,3);
94 else if(maze[i-1][j])
95 DFS_RF(i-1,j,0);
96 else if(maze[i][j-1])
97 DFS_RF(i,j-1,1);
98 else if(maze[i+1][j])
99 DFS_RF(i+1,j,2);
100 break;
101 }
102 case 1:
103 {
104 if(maze[i-1][j])
105 DFS_RF(i-1,j,0);
106 else if(maze[i][j-1])
107 DFS_RF(i,j-1,1);
108 else if(maze[i+1][j])
109 DFS_RF(i+1,j,2);
110 else if(maze[i][j+1])
111 DFS_RF(i,j+1,3);
112 break;
113 }
114 case 2:
115 {
116 if(maze[i][j-1])
117 DFS_RF(i,j-1,1);
118 else if(maze[i+1][j])
119 DFS_RF(i+1,j,2);
120 else if(maze[i][j+1])
121 DFS_RF(i,j+1,3);
122 else if(maze[i-1][j])
123 DFS_RF(i-1,j,0);
124 break;
125 }
126 case 3:
127 {
128 if(maze[i+1][j])
129 DFS_RF(i+1,j,2);
130 else if(maze[i][j+1])
131 DFS_RF(i,j+1,3);
132 else if(maze[i-1][j])
133 DFS_RF(i-1,j,0);
134 else if(maze[i][j-1])
135 DFS_RF(i,j-1,1);
136 break;
137 }
138 }
139 return;
140 }
141
142 void BFS_MSS(int i,int j) //最短路搜索
143 {
144 bool vist[41][41]={false};
145 SE queue[1600];
146 int head,tail;
147
148 queue[head=0].r=i;
149 queue[tail=0].c=j;
150 queue[tail++].depth=1; //当前树深标记,这是寻找最短路的关键点
151
152 vist[i][j]=true;
153
154 while(head<tail)
155 {
156 SE x=queue[head++];
157
158 if(x.r==e.r && x.c==e.c)
159 {
160 cout<<x.depth<<endl;
161 return;
162 }
163
164 if(maze[x.r][x.c-1] && !vist[x.r][x.c-1])
165 {
166 vist[x.r][x.c-1]=true;
167 queue[tail].r=x.r;
168 queue[tail].c=x.c-1;
169 queue[tail++].depth=x.depth+1;
170 }
171 if(maze[x.r-1][x.c] && !vist[x.r-1][x.c])
172 {
173 vist[x.r-1][x.c]=true;
174 queue[tail].r=x.r-1;
175 queue[tail].c=x.c;
176 queue[tail++].depth=x.depth+1;
177 }
178 if(maze[x.r][x.c+1] && !vist[x.r][x.c+1])
179 {
180 vist[x.r][x.c+1]=true;
181 queue[tail].r=x.r;
182 queue[tail].c=x.c+1;
183 queue[tail++].depth=x.depth+1;
184 }
185 if(maze[x.r+1][x.c] && !vist[x.r+1][x.c])
186 {
187 vist[x.r+1][x.c]=true;
188 queue[tail].r=x.r+1;
189 queue[tail].c=x.c;
190 queue[tail++].depth=x.depth+1;
191 }
192 }
193 return;
194 }
195
196 int main(int i,int j)
197 {
198 int test;
199 cin>>test;
200 while(test--)
201 {
202 int direction; //起点S的初始方向
203 int w,h; //size of maze
204 cin>>w>>h;
205
206 /*Initial*/
207
208 Lstep=1;
209 Rstep=1;
210 memset(maze,false,sizeof(maze));
211
212 /*Structure the Maze*/
213
214 for(i=1;i<=h;i++)
215 for(j=1;j<=w;j++)
216 {
217 char temp;
218 cin>>temp;
219 if(temp=='.')
220 maze[i][j]=true;
221 if(temp=='S')
222 {
223 maze[i][j]=true;
224 s.r=i;
225 s.c=j;
226
227 if(i==h)
228 direction=0;
229 else if(j==w)
230 direction=1;
231 else if(i==1)
232 direction=2;
233 else if(j==1)
234 direction=3;
235 }
236 if(temp=='E')
237 {
238 maze[i][j]=true;
239 e.r=i;
240 e.c=j;
241 }
242 }
243
244 /*Left First Search*/
245
246 switch(direction)
247 {
248 case 0: {DFS_LF(s.r-1,s.c,0); break;}
249 case 1: {DFS_LF(s.r,s.c-1,1); break;}
250 case 2: {DFS_LF(s.r+1,s.c,2); break;}
251 case 3: {DFS_LF(s.r,s.c+1,3); break;}
252 }
253 cout<<Lstep<<' ';
254
255 /*Right First Search*/
256
257 switch(direction)
258 {
259 case 0: {DFS_RF(s.r-1,s.c,0); break;}
260 case 1: {DFS_RF(s.r,s.c-1,1); break;}
261 case 2: {DFS_RF(s.r+1,s.c,2); break;}
262 case 3: {DFS_RF(s.r,s.c+1,3); break;}
263 }
264 cout<<Rstep<<' ';
265
266 /*Most Short Step Search*/
267
268 BFS_MSS(s.r,s.c);
269
270 }
271 return 0;
272 }