HDU 4744 Starloop System（最小费用最大流）（2013 ACM/ICPC Asia Regional Hangzhou Online）

Description

At the end of the 200013  ^th year of the Galaxy era, the war between Carbon-based lives and Silicon civilization finally comes to its end with the Civil Union born from the ruins. The shadow fades away, and the new-born Union is opening a new page. 

Although the war ended, the affect of the war is far from over. Now the council is busy fixing the transportation system. Before the war, all the stars were connected with artificial wormholes which were destroyed during the war. At the same time, natural wormholes are breaking down with the growing traffic. A new traffic system is on the schedule. 

As two civilizations combine, the technology integrates. Scientists find a new traffic system called the Starloop System. 

This system is made up of several starloops. People build a starway to connect two stars. A startloop is a closed path with no repetitions of stars or starways allowed, other than the repetition of the starting and ending star. And a starloop contains at least two starts and two starways. A startloop's cost is the sum of the length of all the starways in it. Length of a starway connecting two stars is floor(x), which x is the euclidean distance between two stars. You can build more than one starway between any two stars, but one starway can only belongs to one starloop. 



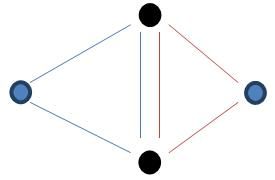
As the picture above shows, there are two starloops. One is blue and the other one is brown. 

As a starloop is set up, each star on the starloop will get a unit of star-energy. So the two blue stars can get one unit of star-energy, and at the same time the black two stars can get two units because they both belong to two starloops. When a star earns a certain number of energy units, the transporter on that star will be activated. One can easily travel between any two stars whose transporter is activated. 

Now the council wants to know the minimal cost to build a starloop system on all the stars . In other words, every star's transporter should be activated

 

Input

There are multiple test cases. 
For each test case: 
There is a line with one integer n which is the number of stars. 

The following n lines each describes a star by four integers xi, yi, zi and wi, defined as the spatial coordinate and the number of energy units the star needs to activate the transporter. Please NOTE that getting more than wi energy units will put the star in a dangerous situation, so it is not allowed. 
The input ends with n = 0. 
1<=n<=100
|xi|,|yi|,|zi|<=200
wi<=50

Output

For each test case, output one line that contains an integer equals to the minimal cost you can get. If there is no solution, just output -1;

 

题目大意：空间上n个点，每个点有一个wi。每对点的距离定义为floor(欧拉距离)，每对点之间建一条边的费用为两点间的距离，每对点之间可以建多条边。现要求对每一个点 i ，都在 wi 个简单环上（每个点每条边都只经过一次），每条边只能属于一个简单环（随你选择属于哪个），简单环的费用为sum{每条边的费用}，问最小的建环费用。

思路：每个点拆成a、b两个点，从附加源点S到a连一条边，容量为wi，费用为0；从b到附加汇点T连一条边，容量为wi，费用为0。每两个点i, j之间，ai到bj连一条边，bi到aj连一条边，费用均为i, j的距离，容量均为无穷大。若最大流=sum{wi}，那么有解，输出最小费用，否则输出-1。

我也不会证明，我比赛的时候觉得这样应该可以构造出解，但是没写……可是后来比赛结束试了一下1A了T_T……等我想到为什么是对的再回来补证明……

 

好了我回来补证明了，经过本菜的苦思冥想，最终我认为，我看错题了，打开题目再看了一次，真的看错题了……我当时想那样建图只是直觉觉得那样可以过样例没想到能AC……

好了正题，这里准备借用无源汇上下界网络流的思想，不会的可以翻我以前的blog

对每一个点，拆成两个点a、b，b到a连一条边，容量上界为wi，下界为wi，对不同的两个点，分别a到b连一条边，容量上界为正无穷大，下界为零。

那么，做无源汇上下界网络最小费用流，当且仅当下界都满的时候，对于每个点 i （即边bi→ai）都在 wi 个简单环上。

这是因为对于无源汇上下界网络流，只能以环的形式进行增广，因为要求费用尽量小，那么每次找出的环一定都是简单环（多过几个就不划算了）。

而流每增加1，就等同于建一个环的边，所以每条边都只会属于一个简单环。

简化一下就是最初所说的建图了。

 

代码（500MS）：

  1 #include <cstdio>

  2 #include <queue>

  3 #include <cstring>

  4 #include <cmath>

  5 using namespace std;

  6 

  7 const int MAXN = 210;

  8 const int MAXE = 210 * 210 * 2;

  9 const int INF = 0x3f3f3f3f;

 10 

 11 struct ZKW_flow{

 12     int st, ed, ecnt, n;

 13     int head[MAXN];

 14     int cap[MAXE], cost[MAXE], to[MAXE], next[MAXE];

 15 

 16     void init(){

 17         memset(head, 0, sizeof(head));

 18         ecnt = 2;

 19     }

 20 

 21     void addEdge(int u, int v, int cc, int ww){

 22         cap[ecnt] = cc; cost[ecnt] = ww; to[ecnt] = v;

 23         next[ecnt] = head[u]; head[u] = ecnt++;

 24         cap[ecnt] = 0; cost[ecnt] = -ww; to[ecnt] = u;

 25         next[ecnt] = head[v]; head[v] = ecnt++;

 26     }

 27 

 28     int dis[MAXN];

 29 

 30     void SPFA(){

 31         for(int i = 1; i <= n; ++i) dis[i] = INF;

 32         priority_queue<pair<int, int> > Q;

 33         dis[st] = 0;

 34         Q.push(make_pair(0, st));

 35         while(!Q.empty()){

 36             int u = Q.top().second, d = -Q.top().first;

 37             Q.pop();

 38             if(dis[u] != d) continue;

 39             for(int p = head[u]; p; p = next[p]){

 40                 int &v = to[p];

 41                 if(cap[p] && dis[v] > d + cost[p]){

 42                     dis[v] = d + cost[p];

 43                     Q.push(make_pair(-dis[v], v));

 44                 }

 45             }

 46         }

 47         for(int i = 1; i <= n; ++i) dis[i] = dis[ed] - dis[i];

 48     }

 49 

 50     int minCost, maxFlow;

 51     bool use[MAXN];

 52 

 53     int add_flow(int u, int flow){

 54         if(u == ed){

 55             maxFlow += flow;

 56             minCost += dis[st] * flow;

 57             return flow;

 58         }

 59         use[u] = true;

 60         int now = flow;

 61         for(int p = head[u]; p; p = next[p]){

 62             int &v = to[p];

 63             if(cap[p] && !use[v] && dis[u] == dis[v] + cost[p]){

 64                 int tmp = add_flow(v, min(now, cap[p]));

 65                 cap[p] -= tmp;

 66                 cap[p^1] += tmp;

 67                 now -= tmp;

 68                 if(!now) break;

 69             }

 70         }

 71         return flow - now;

 72     }

 73 

 74     bool modify_label(){

 75         int d = INF;

 76         for(int u = 1; u <= n; ++u) if(use[u])

 77             for(int p = head[u]; p; p = next[p]){

 78                 int &v = to[p];

 79                 if(cap[p] && !use[v]) d = min(d, dis[v] + cost[p] - dis[u]);

 80             }

 81         if(d == INF) return false;

 82         for(int i = 1; i <= n; ++i) if(use[i]) dis[i] += d;

 83         return true;

 84     }

 85 

 86     int min_cost_flow(int ss, int tt, int nn){

 87         st = ss, ed = tt, n = nn;

 88         minCost = maxFlow = 0;

 89         SPFA();

 90         while(true){

 91             while(true){

 92                 for(int i = 1; i <= n; ++i) use[i] = 0;

 93                 if(!add_flow(st, INF)) break;

 94             }

 95             if(!modify_label()) break;

 96         }

 97         return minCost;

 98     }

 99 } G;

100 

101 struct Point {

102     int x, y, z, w;

103     void read() {

104         scanf("%d%d%d%d", &x, &y, &z, &w);

105     }

106     int operator * (const Point &rhs) const {

107         double xx = x - rhs.x, yy = y - rhs.y, zz = z - rhs.z;

108         return (int)sqrt(xx * xx + yy * yy + zz * zz);

109     }

110 };

111 

112 Point a[MAXN];

113 int n;

114 

115 int main() {

116     while(scanf("%d", &n) != EOF && n) {

117         int sumw = 0;

118         for(int i = 1; i <= n; ++i) a[i].read(), sumw += a[i].w;

119         G.init();

120         int ss = 2 * n + 1, tt = ss + 1;

121         for(int i = 1; i <= n; ++i) {

122             G.addEdge(ss, i, a[i].w, 0);

123             G.addEdge(i + n, tt, a[i].w, 0);

124             for(int j = i + 1; j <= n; ++j) {

125                 int cost = a[i] * a[j];

126                 G.addEdge(i, j + n, INF, cost);

127                 G.addEdge(j, i + n, INF, cost);

128             }

129         }

130         int ans = G.min_cost_flow(ss, tt, tt);

131         if(sumw != G.maxFlow) ans = -1;

132         printf("%d\n", ans);

133     }

134 }

View Code