《挑战程序设计竞赛》 读后感
最近要开始准备面试找工作,算法是准备的重中之重,舍友推荐了《挑战程序设计竞赛》这本书。花了一周的时间大体过了一遍,该书真切地让我理解了“智商是硬伤”这句话的含义。我对它的评价是:如果智商小于120,只看前两章就够了;智商大于120小于150,三四章的简单章节还是可以看一下的;智商大于150,看完本书问题不大。望大家量力而为,否则你的自信心会遭受严重的打击。
下面把自己看懂的,并感觉比较重要的内容整理下来,并提供更多扩展资料,希望对复习算法的同学有帮助。
准备篇
1.5 运行时间
概述编写的目的是面向ACM程序设计竞赛,不可避免的要涉及复杂度和运行时间的问题,本节给出了解决问题算法选择的依据。假设题目描述中给出的限制条件为n<=1000,针对O(n2)的算法将会执行大于106次。如果时间限制是1s,则有下述结论:
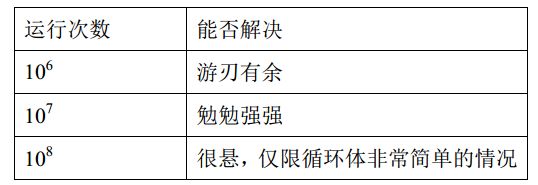
上述结论表明,针对O(n2)的算法,n<=1000可以在时限内解决,但是如果n<=10000,则超时的可能性非常大,这就启示我们要寻找新的算法降低算法复杂度,否则将不能AC。
1.6 三角形
给定N个边,任选三边构成三角形,输出最大的周长。通过三层循环可以解决,但是复杂度为O(n3)。如果利用3.2节的折半枚举技巧可以在O(n2logn)的时间内解决:首先将所有的边排序,复杂度为O(nlogn);然后两层循环得到任意两条边的距离之和;最后二分查找,找到能构成三角形的最大边。文中说还有O(nlogn)的算法,我不知道,希望有人能告诉我。折半枚举这个技巧非常有用,可以解决一大类问题,抽签问题即是一个非常好的例子。
初级篇
2.1 穷竭搜索
1. 基础
栈的头文件<stack>,常用方法:push,top,pop;队列的头文件<queue>,常用方法:push,front,pop。
2. 深搜
部分和问题:给定n个数,选出若各个其和是否为k。代码:
int a[MAX_N];
int n,k;
//已经从前i项得到了sum,然后对i项之和的进行分支
bool dfs(int i,int sum){
if(i==n) return sum==k;
if(dfs(i+1,sum)) return true;
if(dfs(i+1,sum+a[i])) return true;
return false;
}
void solve() {
if(dfs(0,0)) printf(“Yes\n”);
else printf(“No\n”);
}
该代码具有普遍性,能解决非常多的问题,如果不考虑复杂度01背包也可以按照这个思路解决。深搜按照回溯的策略去遍历问题的解空间,部分和问题和01背包问题的解都是原数组的子集,所以其解空间构成了一个二叉树。除了二叉树形式的解空间,还有很多问题的解空间是k叉树,例如八皇后问题,每一行的皇后有八个位置可以选择,解空间构成了一个八叉树。不管是几叉树,代码结构类似。此外《编程之美》第3.2节的电话号码对应英语单词也属于此类结构,只不过每一层的叉树不一样。解空间是k叉树时,遍历的复杂度是O(kn)。由于复杂度非常高,在遍历的过程中往往伴随着解空间的剪枝。
还有很多问题的解空间不是原数据的子集,而是一个排列,此时解空间是一个排列树。最具代表性的一个例子是旅行商问题,其每一层的树节点都在逐次减一,所以其复杂度是O(n!)。
还有一些问题不属于上面的两类情况,例如n皇后问题,其复杂度变为O(nn)。还有一个例子是《编程之美》1.3节的烙饼排序问题,也是一个复杂度变为O(nn)的深搜问题。不管属于哪一类,它们的代码结构比较类似:
dfs(int i){
//1 输出结果
if(i==n) printf();
//2 剪枝
//3遍历下一层
for(int j=0;j<k;j++){//子集树
for(int j=i;j<=n;j++){//排列树
for(int j=0;j<n;j++){//n叉树
dfs(i+1);
}
}
如果是最优化问题,利用深搜的方法遍历解空间都可以获得正确解。但是很多问题都有其更优的解法。不过有时题目的参数限制会迫使我们选择深搜遍历解空间。例如,01背包问题的动态规划解法复杂度为O(nW),其中n为物品数,W为背包容量。如果物品数n不是很大,但是背包容量W非常大,则利用动态规划求解可能不如深搜遍历解空间的算法快(来源于:背包问题九讲)。但是如果n很大,则肯定不能用深搜来解决,即使加上剪枝也不行。在遇到一个实际问题时,我们可以通过给定的参数限制去判断是否能直接采用深搜去解决问题,如果运算量小于106,则可以采用;如果运算量在107附近,加上剪枝则应该可以通过;如果运算量大于108,则需要考虑其他算法。事实上,针对这些复杂度很高的深搜算法,往往都会有相应的复杂度较低的动态规划算法。例如,01背包的动态规划算法复杂度为O(nW),旅行商问题的状态压缩动态规划算法复杂度为O(n22n)。
如果解空间不是树,例如寻找连通构件的问题,其解空间就是矩阵,我们就可以按照遍历矩阵的方法去寻找解。图上的连通构件问题可以通过遍历所有的点来解决。此问题广搜同样可以解决。
3. 广搜
广搜按照距开始状态由近及远的顺序进行搜索,可以很容易地用来求解最短路径、最少操作之类问题的答案。这是因为深搜(隐式地)利用了栈进行计算,但是广搜利用了队列。分支定界即是采用广搜的一个思想,但是采用队列保存状态使其耗费的内存远大于深搜。
利用广搜求解的典型问题包括:迷宫的最短路径,二叉树的逐层遍历。
2.2 贪心
1. 区间调度问题
n个工作,每个工作开始于si,结束于ti,求最多可以参与多少项工作。该问题有一个贪心解:在可选的工作中,每次都选取结束时间最早的工作。
还有另外一个问题:如果将这些工作全部分配给一些工人,最少需要几个工人。该问题也有一个贪心解,复杂度为O(nlogn):首先按照si的递增次序排列各个工作,然后构造一个已安排工作的工人可以最早开始工作的最小堆,将这些任务按照si分配给最小堆的最小值,并修改其最早开始时间。最后被安排工作的工人数即是最少的工人数。
将问题再变一下,如果工人数固定为k,n项工作每项工作的时间为si,求最短完成时间。这个问题就变成一个NP复杂的问题。一种解决方案是利用上面介绍的深搜去遍历解空间:解空间是一个k叉树,表示某个工作分配给哪一个工人;树共有n层,每一个叶节点表示一个可能的任务分配,求最小的叶节点。
2.3 动态规划(DP)
1. 注意事项
虽然memset按照1字节为单位对内存进行填充,-1的每一位二进制都是1,所以可以像0一样用memset进行初始化。通过使用memset可以快速的对高维数组等进行初始化,但是需要注意无法完成初始化成1之类的数值。如果想对一个高维数组初始化为1或者无穷,可以采用fill函数,该函数按照数据类型进行赋值。
全局数组的内容会被初始化为0,如果程序运行一次无需初始化;但是如果需要多次运行,必须要进行初始化。
2. 背包问题
令dp[i+1][j]表示从前i个物品中选出总重量不超过j的物品时总价值的最大值,则背包问题的通用递推式为:

其中,01背包问题中k=0或1;完全背包问题中, 多重背包问题中,
多重背包问题中,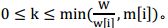 上述代码的复杂度:01背包为O(nW),完全背包为O(nW2)。但事实上,完全背包问题的递推式还可以简化为:
上述代码的复杂度:01背包为O(nW),完全背包为O(nW2)。但事实上,完全背包问题的递推式还可以简化为:

此时也可以在O(nW)的时间内解决。标准的01背包问题代码为:
void solve(){
for(int i=0;i<n;i++){
for(int j=0;j<=W;j++){
if(j<w[i]) dp[i+1][j]=dp[i][j];
else dp[i+1][j]=max(dp[i][j], dp[i][j-w[i]]+v[i]);
}
}
printf(“%d\n”,dp[n][W]);
}
标准的完全背包代码:
void solve(){
for(int i=0;i<n;i++){
for(int j=0;j<=W;j++){
if(j<w[i]) dp[i+1][j]=dp[i][j];
else dp[i+1][j]=max(dp[i][j], dp[i+1][j-w[i]]+v[i]);
}
}
printf(“%d\n”,dp[n][W]);
}
两者之间结构一样,只有一点递推式的赋值不一样。由于我们只需要最后的一个值,而且我们从递推式可以看出:01背包中每一行的元素只依赖于上一行,完全背包中每一行只依赖上一行的一个元素和本行的前面元素。所以我们可以对背包问题的空间进行优化,只需要使用一个一维数组实现。01背包问题的空间优化代码:
int dp[MAX_W+1];
void solve(){
for(int i=0;i<n;i++){
for(int j=W;j>=w[i];j--){
dp[j]=max(dp[j], dp [j-w[i]]+v[i]);
}
}
printf(“%d\n”,dp[W]);
}
完全背包问题的空间优化代码:
int dp[MAX_W+1];
void solve(){
for(int i=0;i<n;i++){
for(int j=w[i];j<=W;j++){
dp[j]=max(dp[j], dp [j-w[i]]+v[i]);
}
}
printf(“%d\n”,dp[W]);
}
可以看出两个背包问题的差异只是在背包容量的遍历顺序上。由此可以将它们抽象出来形成一个对背包容量更普遍的遍历(摘自背包问题九讲):
ZeroOnePack(weight,value) for w from W to weight do f[w]=max(f[w],f[w-weight]+value) CompletePack(weight,value) for w from weight to W do f [w] = max(f [w]; f [w-weight] + value)
根据上面两个背包问题的伪代码,多重背包问题就可以按照下面的思路解决:
MultiplePack(weight; value; amount)
if weight * amount > W
then CompletePack(cost; weight)
return
k=1 while k < amount
do
ZeroOnePack(k*weight; k*value)
amount=amount-k
k=k*2
ZeroOnePack(amount*weight; amount*value)
上面解决多重背包的方法是将其每一个物品分别分解成完全背包或者是01背包问题来解决,虽然不是最低复杂度,但是效率也很高。
将上述三种背包混合就得到混合背包问题,伪代码为:
for i from 1 to N
do if 第i件物品属于01背包
then ZeroOnePack(w[i]; v[i])
else if 第i件物品属于完全背包
then CompletePack(w[i]; v[i])
else if 第i件物品属于多重背包
then MultiplePack(w[i]; v[i]; m[i])
关于初等背包的另一个需要注意问题是初始化问题。有的题目要求“恰好装满背包”时的最优解,有的题目则并没有要求必须把背包装满。一种区别这两种问法的实现方法是在初始化的时候有所不同。如果是第一种问法,要求恰好装满背包,那么在初始化时除了f[0]为0,其它f[1..W]均设为-∞,这样就可以保证最终得到的f[N]是一种恰好装满背包的最优解。如果并没有要求必须把背包装满,而是只希望价格尽量大,初始化时应该将f[0..W]全部设为0。一个“恰好装满背包”的实例是编程之美1.6节的饮料供应问题。
关于背包问题的高级主题和详细介绍大家可以看: 背包问题九讲。
2.4 数据结构
1. 基本结构
STL中的优先队列为priority_queue,头文件为<queue>,常用操作为:push,top,pop,empty,size。该优先队列默认pop的是最大值,如果想pop最小值(最小堆),则需要指明比较函数:priority_queue<int,vector<int>,greater<int>> que;
STL中实现二叉搜索树的容器有set和map,头文件分别为<set>和<map>。set的常用函数为:insert(重复插入报错),find,erase(删除),start,end(最后一个元素之后),count。允许存放重复键值的容器为multiset和multimap。
2. 并查集
可以根据重量规则和高度规则构造并查集。算法导论和很多acmer都采用了高度规则构造并查集,但是高度规则在路径压缩的过程中不修改高度,这其实是错误的,因而个人感觉基于重量规则的并查集更好用。重量规则的含义是:若树i节点数小于树j的节点数,则将j作为i的父节点;否则,将i作为j的父节点。也即重量规则根据树包含的节点个数来进行union。基于重量规则的并查集代码为:
bool root[MAX_N];
int parent[MAX_N];
void init(int n){
for(int i=0;i<n;i++){
parent[i]=1;//每一个树都只有一个元素
root[i]=true;
}
}
int find(int e){
int j=e;
while(!root[j]) j=parent[j];
int f=e;
while(f!=e) {
int pf=parent[f];
parent[f]=j;
f=pf;
}
return j;
}
void union(int i,int j) {
if(parent[i]<parent[j]) {
//只有是根,parent才保存树的元素个数,否则指向父节点
parent[j]+=parent[i];
root[i]=false;
parent[i]=j;
}
else{
parent[i]+=parent[j];
root[j]=false;
parent[j]=i;
}
}
并查集的一个最典型应用是Kruskal算法解决最小生成树(MST)问题。
2.5 图
1. 图着色问题
书中介绍了二分图的判定问题,代码如下:
vector<int> G[MAX_V];//图
int V;
int color[MAX_V];
bool dfs(int v,int c){
color[v]=c;
for(int i=0;i<G[v].size();i++){
if(color[G[v][i]]==c) return false;
if(color[G[v][i]]==0 && !dfs(G[v][i],-c)) return false;
}
return true;
}
void solve(){
for(int i=0;i<V;i++){
if(!dfs(i.1)) {printf(“No\n”); return;
}
printf(“Yes\n”);
}
一般情况下的最小图着色问题是一个NP复杂问题,但是我们可以通过一个简单的二分策略求解:最小着色数肯定在范围1到INF之间,我们通过二分查找判断每一个着色是是否能满足条件;判断一个给定的着色数是否满足条件可以仿照上面的代码实现。一个关于图着色的实例是编程之美1.9节的高效率地安排见面会。
2. Dijkstra和Prim算法
两者具有类似的代码结构,所以将其放在一起。Dijkstra算法求解没有负边的单源最短路径问题。其算法思想是:找到最短距离已经确定的顶点,从它出发更新相邻顶点的最短距离。代码如下:
struct edge{int to, cost;};//图的边
typedef pair<int,int> P;//保存的结果,first为最短距离,second为相应顶点
int V;
vector<edge> G[MAX_V];
int d[MAX_V];
void dijkstra(int s){
priority_queue<P,vector<P>,greater<P>> que;
fill(d,d+V,INF);
d[s]=0;
que.push(P(0,s));
while(!que.empty()){
P p=que.top(); que.pop();
int v=p.second;
for(int i=0;i<G[v].size;i++){
edge e=G[v][i];
if(d[e.to]>d[v]+e.cost){
d[e.to]=d[v]+e.cost;
que.push(P(d[e.to],e.to));
}
}
}
}
Prim算法是求MST,它和Dijkstra算法十分相似,都是从某个顶点出发,不断添加边的算法。
2.6 简单的数学问题
1. 埃氏筛法
判断一个数是否是素数,只需要判断小于等于n的开方的整数能否整除n即可。如果需要求所有小于n的素数,则需要埃氏筛法。思想很简单,代码如下:
int prime[MAX_N];
bool is_prime[MAX_N+1];
int sieve(int n){
int p=0;
for(int i=0;i<=n;i++) is_prime[i]=true;
is_prime[0]=is_prime[1]=false;
for(int i=2;i<=n;i++){
if(is_prime[i]){
prime[p++]=I;
for(int j=2*i;j<=n;j+=i) is_prime[j]=false;
}
}
return p;
}
快速幂运算
在求xn时,我们通过将n按照二进制分解,可以获得一个求幂的快速算法:
typedef long long ll;
ll mod_pow(ll x,ll n,ll mod){
ll res=1;
while(n>0){
if(n&1) res=res*x%mod;
x=x*x%mod;
n>>=1;
}
return res;
}
求幂的快速算法在求矩阵的幂时也可以采用。
总体上,第二章的难度中等偏上,只要能多思考,绝大多数问题都能看懂。
中级篇
3.1 二分搜索
通过该节让我真切明白二分搜索的应用价值远远大于其看上去的样子,所以该节内容值得仔细研究。另一方面,二分搜索的难度也不像其看上去的样子,网上说“80%的程序员写不对二分查找”并非谣言。
1. lower_bound
给定一个单调不下降数列和一个数k,求满足ai>=k的最小i。
首先看一下第n/2个值。如果a[n/2]>=k,则可以知道解的范围不大于n/2。反之,如果a[n/2]<k,就可以知道解大于n/2。代码如下:
int n,k;
int a[MAX_N];
void lower_bound(){
int lb=-1,ub=n;
while(ub-lb>1){
int mid=(lb+ub)/2;
if(a[mid]>=k) ub=mid;
else lb=mid;
}
printf(“%d\n”,ub);
}
上述算法不仅能找到要寻找的值,而且返回的是一系列值中的最小值,可以用来求解“满足某个条件C(x)的最小的x”问题。STL将上述代码以lower_bound函数的形式实现,不过需要注意的是该函数返回的是一个位置指针,可以通过解引用来获取元素值,还可以通过与数组起点相减获得位置下标。与此类似的还有函数upper_bound函数,它返回ai>k的最小i。利用这两个函数我们就可以求数组中元素k出现的次数:
upper_bound(a,a+n,k)-lower_bound(a,a+n,k);
后面三个小节讲了二分搜索的应用,它们都依赖下面的基本原理:问题的正确解为X,当给定的解小于等于X时,都能满足要求;当给定的解大于X时,解不满足要求。也即解空间以X为分界,分成正确的和错误的两个子集。
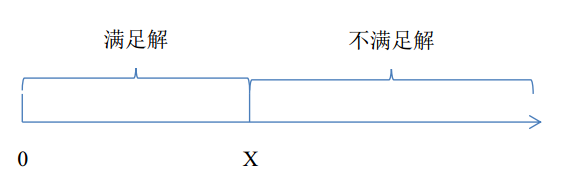
解题流程都是:判断一个给定的数x是否满足条件,若满足条件就放大x,否则就减小x,通过不停地减小搜索区间找到最后的值。对于x是浮点数的情况,可以通过设定一个遍历次数的上届完成二分搜索。由于二分搜索每次将区间减小一半,所以100次遍历即可以将区间减到任意精度。对于x是整数的情况,可以简单的选取lb为问题的解。这是因为lb总是问题的解,ub总不是问题的解,当两者距离等于1时,搜索结束。此时lb还是问题的解,ub依旧不是问题的解。此外,前面介绍的图最小着色问题也是用了二分搜索的思想。
3.2 常用技巧(一)
1. 尺取法
给定一个长度为n的正整数数列,以及整数S。求总和不小于S的连续子序列的长度最小值。
可以按照如下方法解决该问题:
(1) 设置两个指针s和t,一开始都指向数列第一个元素,此外sum=0,res=0;
(2) 只要sum<S,就将sum增加一个元素,t加1;
(3) 直到sum>=S,更新res=min(res,t-s);
(4) 将sum减去一个元素,s加1,执行(2)。
上述流程反复地推进区间的开头和末尾,来求取满足条件的最小区间。代码如下:
void solve(){
int res=n+1;
int s=0,t=0,sum=0;
for(;;){
while(t<n &&sum<S) sum+=a[t++];
if(sum<S) break;
res=min(res,t-s);
sum-=a[s++];
}
if(res>n) res=0;
}
尺取法在别的地方又被称为滑动窗口或者蠕虫算法,应用很广。让人看不明白的编程之美3.5节最短摘要的生成也是采用了此法。
2. 位运算
常用集合运算的位运算:
(1) 空集:0;
(2) 只含有第i个元素的集合:1<<i;
(3) 含有全部n个元素的集合:(1<<n)-1;
(4) 判断第i个元素是否属于集合S:if(S>>i&1);
(5) 向集合加入第i个元素:S|1<<i;
(6) 从集合除去第i个元素:S|~(1<<i);
(7) 集合S和T的并集:S|T;
(8) 集合S和T的交集:S&T。
遍历集合的所有子集可以通过如下代码完成:
for(int i=0;i<1<<n;i++) {}//每一个i都是S的一个子集
遍历某个特定集合sup的子集,例如遍历01101101的子集,可以通过如下代码完成:
int sub=sup;
do{
//子集处理
sub=(sub-1)&sup
while(sub!=sup);
枚举所有大小为K的子集方法:
int comb=(1<<k)-1;
while(comb<1<<n){
//处理代码
int x=comb&-comb,y=comb+x;
comb=((comb&~y)/x>>1)|y;
}
3.5 网络流
很多问题都可以转行为二分图匹配,所以二分图匹配的匈牙利算法要掌握。在网络流中有四个概念需要强调:
- 匹配:在G中两两没有公共端点的边集合M
- 边覆盖:G中的任意顶点都至少是F中某条边的端点的边集合F
- 独立集:在G中两两互不相连的顶点集合S
- 顶点覆盖:G中的任意边都有至少一个端点属于S的顶点集合S
以上四个概念满足如下关系:
- 对于不存在孤立点的图,|最大匹配|+|最小边覆盖|=|V|
- |最大独立集|+|最小顶点覆盖|=|V|
利用这些关系,对于最大匹配和最小边覆盖,最大独立集和最小顶点覆盖,只要能求解其中一个,另一个问题也就得到解决。最大独立集问题是NP复杂的问题,但是针对二分图,有如下等式成立:
|最大匹配|=|最小顶点覆盖|
总体上,第三章的难度很大,本人只能理解其中的一小部分,哎……
高级篇
4.1 数学问题
在此只介绍容斥原理。给定一个数列长度为m,求1到n中的整数至少能整除a中的一个元素的数有几个。此问题即是求容斥原理的公式,计算方法为:累加所有能整除一个元素的个数,减去所有两个元素的公倍数,……。代码如下:
typedef long long ll;
int a[MAX_N];
int n,m;
void solve(){
ll res=0;
//变量m个元素的所有子集
for(int i=0;i<(1<<m);i++){
int num=0;
for(int j=i;j!=0;j>>=1)num+=j&1;//统计该子集有多少个元素
ll lcm=1;
for(int j=0;j<m;j++){//根据二进制中1的位置判断哪个元素出现
if(i>>j&1){
lcm=lcm/gcd([lcm,a[j]])*a[j];//求一个数组的最小公倍数
if(lcm>n) break;
}
}
if(num%2==0) res-=n/lcm;
else res+=n/lcm;
}
printf("%d\n”,res);
}
4.3 图论大师
1. 强连通分量
强连通分量分解可以通过两次DFS实现。第一次DFS时,选取任意顶点作为起点,遍历所有尚未访问过的顶点,并在回溯前给顶点标号。对剩余尚未访问过的顶点不断重复上述过程。完成标号后,越接近图的尾部,顶点的标号越小。第二次DFS时,先将所有边反向,然后以标号最大的顶点为起点进行DFS。这样DFS所遍历的顶点集合就构成了一个强连通分量。之后,只要还有尚未访问的顶点,就从中选取标号最大的顶点不断重复上述过程。求图的强连通分量非常重要,需要熟悉代码:
int V;//定点数
vector<int> G[MAX_V];//图的邻接表表示
vector<int> rG[MAX_V];//把边反向后的图
vector<int> vs;//后序遍历顺序的顶点列表
bool used[MAX_V];//访问标记
int cmp[mAX_V];//所属强连通分量的拓扑序
void add_edge(int from,int to){
G[from].push_back(to);
G[to].push_back(from);
}
void dfs(int v){
used[v]=true;
for(int i=0;i<G[v].size();i++){
if(!used[G[v][i]]) dfs(G[v][i]);
}
vs.push_back(v); //起点放在最后
}
void rdfs(int v,int k){
used[v]=true;
cmp[v]=k;
for(int i=0;i<rG[v].size();i++){
if(!used[rG[v][i]]) rdfs(G[v][i],k);
}
}
int scc(){
memset(used,0,sizeof(used));
vs.clear();
for(int v=0;v<V;v++){
if(!used[v]) dfs(v);
}
memset(used,0,sizeof(used));
int k=0;
for(int i=vs.size()-1;i>=0;i--){
if(!used[vs[i]])) rdfs(vs[i],k++);
}
return k;
}
2. 2-SAT
给定一个bool方程,判断是否存在一组布尔变量的真值指派使整个方程为真的问题,称为布尔方程的可满足性问题(SAT),该问题是一个NP问题。合取范式如下:

如果合取范式中的每个子句中的变量个数都不超过两个,则对应的SAT问题又被称为2-SAT问题,该问题可以在线性时间内解决。
解决方法是利用蕴含操作  将每个子句
将每个子句 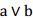 改为
改为 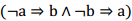 这样原布尔公式就变成只有与运算的公式,每一个子句都是一个蕴含运算。对每个布尔变量x,构造两个顶点分别代表x和
这样原布尔公式就变成只有与运算的公式,每一个子句都是一个蕴含运算。对每个布尔变量x,构造两个顶点分别代表x和  ,以
,以 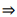 关系为边建立有向图。此时,如果图上的a点能够到达b点的话,就表示当a为真时b也一定为真。因此,同一强连通分量中所含的所有文字的布尔值均相同。
关系为边建立有向图。此时,如果图上的a点能够到达b点的话,就表示当a为真时b也一定为真。因此,同一强连通分量中所含的所有文字的布尔值均相同。
如果存在某个布尔变量x,x和  均在同一个强连通分量中,则无法令整个布尔公式的值为真。反之,对于每个布尔变量x,让
均在同一个强连通分量中,则无法令整个布尔公式的值为真。反之,对于每个布尔变量x,让
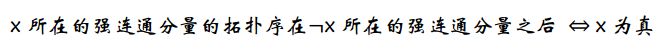
3. LCA
LCA问题是求树中两个节点的最近公共祖先问题,针对不同类型的树和数据结构有不同的算法。
1) 基于二分搜索的方法
记节点v到根的深度为depth(v)。那么,如果节点w是u和v的公共祖先的话,让u向上走depth(u)-depth(w),让v向上走depth(v)-depth(w)步,都将走到w。因此,首先将u和v中较深的节点向上走|depth(u)-depth(v)|不,再一起一步步向上走,直到走到同一个节点,就可以在O(depth(u)+depth(v))时间内求出LCA。这要求的数据结构必须有一个parent域用来指示父节点,此外每个节点都有一个深度信息。
2) 基于RMQ的算法
首先,按从根DFS访问的顺序得到顶点序列vs[i]和对应的深度depth[i]。对于每个顶点v,记其在vs中首次出现的下标为id[i]。这些都可以在O(n)的时间内求得。而LCA(u,v)就是访问u之后到访问v之前所经过顶点中离根最近的那个。假设id[u]<=id[v],那么有
LCA(u,v)=vs[id[u]<=i<=id[v]中令depth(i)最小的i]
而这变成了一个区间最小值查询问题,可以利用RMQ高效地求解。关于RMQ的求解,大家可以查阅网上关于RMQ的ST算法。
针对LCA问题,还有并查集+dfs的tarjan算法,更详细的资料可参考:二叉树中两个节点的最近公共祖先。
4.7 字符串
1. 后缀数组
后缀数组是一个很难的东西,但是很有用,在此不做过多介绍。如果想深入了解它,请参考罗穗骞的算法合集之《后缀数组——处理字符串的有力工具》和算法合集。后缀数组能处理很多问题。例如,字符串匹配,假设已经计算好字符串S的后缀数组,现在要求字符串T在S中出现的位置,只要通过二分搜索就可以在O(|T|log|S|)的时间内完成。如果配合使用最长公共前缀数组,就可以实现更多应用。可以用来寻找两个字符串的最长公共子串和字符串是最长回文子串。
整本书真是越看让人越感到力不从心,心生厌倦,但是一旦掌握一个思想,威力无穷。真心希望励志于算法的人能买下此书,细细研读,必有非常大的收获!
勘误表
1. P113:倒数第二段第一句“min(y1,y2)<=y<=min(y1,x2)”应改为“min(y1,y2)<=y<=min(y1,y2)”。
2. P130:上面问题描述的限制条件“1<=N<=100” 应改为“1<=P<=100”。
3. P132:Millionaire的问题描述第二句“一开始你有x元钱,接着进M轮赌博” 应改为“一开始你有x元钱,接着进行M轮赌博”。
4. P152:一开始第一个求和“f[i]” 应改为“f[j]”;后面两个求和符合的下标“i=”应改为“j=”。
5. P159:第二个公式的条件“是k是偶数时”应改为“当k是偶数时”。
6. P361:第一行“我们统一用n表示数上节点的个数”应改为“我们统一用n表示树上节点的个数”。