二叉树，以及3种遍历

笔试题经常有

 

赶紧搞懂！

 

二叉树：

 

二叉树的遍历(一)  

参考自：  http://blog.163.com/qhx_405/blog/static/6338992620098140352928/

 二叉树的遍历有三种方式，如下：

（1）前序遍历（DLR），首先访问根结点，然后遍历左子树，最后遍历右子树。简记根-左-右。

（2）中序遍历（LDR），首先遍历左子树，然后访问根结点，最后遍历右子树。简记左-根-右。

（3）后序遍历（LRD），首先遍历左子树，然后遍历右子树，最后访问根结点。简记左-右-根。 

  

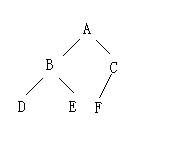
例1：如上图所示的二叉树，若按前序遍历，则其输出序列为      。若按中序遍历，则其输出序列为      。若按后序遍历，则其输出序列为      。

前序：根A，A的左子树B，B的左子树没有，看右子树，为D，所以A-B-D。再来看A的右子树，根C，左子树E，E的左子树F，E的右子树G，G的左子树为H，没有了结束。连起来为C-E-F-G-H,最后结果为ABDCEFGH

中序：先访问根的左子树,B没有左子树，其有右子树D，D无左子树，下面访问树的根A，连起来是BDA。

再访问根的右子树，C的左子树的左子树是F，F的根E，E的右子树有左子树是H，再从H出发找到G，到此C的左子树结束，找到根C，无右子树，结束。连起来是FEHGC,  中序结果连起来是BDAFEHGC

后序：B无左子树，有右子树D，再到根B。再看右子树，最下面的左子树是F，其根的右子树的左子树是H，再到H的根G，再到G的根E，E的根C无右子树了，直接到C，这时再和B找它们其有的根A，所以连起来是DBFHGECA

例2:有下列二叉树，对此二叉树前序遍历的结果为（    ）。

A）ACBEDGFH                                          B）ABDGCEHF

C）HGFEDCBA                                          D）ABCDEFGH

解析：先根A，左子树先根B，B无左子树，其右子树，先根D，在左子树G，连起来是ABDG。 A的右子树，先根C，C左子树E，E无左子树，有右子树为H，C的右子树只有F，连起来是CEHF。整个连起来是B答案 ABDGCEHF。

 

例3：已知二叉树后序遍历是DABEC，中序遍历序列是DEBAC，它的前序遍历序列是(       )  。

A）CEDBA  B）ACBED C）DECAB D）DEABC

解析：由后序遍历可知，C为根结点，由中序遍历可知，C左边的是左子树含DEBA，C右边无结点，知根结点无右子树。先序遍历先访问根C，答案中只有A以C开头，为正确答案。

 

例4：  如下二叉树中序遍历的结果是（　　）。

 

A). ACBDFEG  B). ACBDFGE  C).ABDCGEF  D).FCADBEG

解析:首先中序遍历根F会把左右子树分开，F不会在答案的开头和结尾，排除C和D。在看F的右子树，G是E的右子树，中序遍历先访问E，再访问G，E在G前面，排除B。答案为A。

 

例5：如下二叉树后序遍历的结果是（　　）。

A)  ABCDEF  B) DBEAFC  C)ABDECF  D)DEBFCA

解析：后序的最后一个必须是二叉树的根，快速判断答案为D。

 

参考自： http://www.2cto.com/kf/201209/155011.html

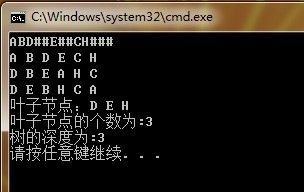
复习下二叉树，创建二叉树，分别以先序，中序，后续三种遍历访问二叉树，输出二叉树的叶子节点及叶子节点的个数，并输出二叉树的高度

[cpp]
#include<iostream> 
#include<cstdio> 
#include<cstring> 
#include<cstdlib> 
using namespace std; 
typedef struct BiTNode 
{    
    char data; 
    struct BiTNode *lchild,*rchild; 
}BiTNode,*BiTree; 
int Max(int x,int y) 
{ 
    return x>y?x:y; 
} 
void Create(BiTree &T)  //先序建一颗二叉树 
{ 
    char ch; 
    scanf("%c",&ch); 
    if(ch=='#') 
    T=NULL; 
    else 
    { 
        T=(BiTNode *)malloc(sizeof(BiTNode)); 
        T->data=ch; 
        Create(T->lchild); 
        Create(T->rchild); 
    } 
} 
void Preorder(BiTree &root)  //先序遍历打印二叉树 
{ 
    if(root!=NULL) 
    { 
        printf("%c ",root->data); 
        Preorder(root->lchild); 
        Preorder(root->rchild); 
    } 
} 
void Inorder(BiTree &root)  //中序遍历打印二叉树 
{ 
    if(root!=NULL) 
    { 
        Inorder(root->lchild); 
        printf("%c ",root->data); 
        Inorder(root->rchild); 
    } 
} 
void Postorder(BiTree &root)  //后续遍历打印二叉树 
{ 
    if(root!=NULL) 
    { 
        Postorder(root->lchild); 
        Postorder(root->rchild); 
        printf("%c ",root->data); 
    } 
} 
void Preorderleaf(BiTree &root) //先序遍历输出叶子节点 
{ 
    if(root!=NULL) 
    { 
        if(root->lchild==NULL&&root->rchild==NULL) 
        printf("%c ",root->data); 
        Preorderleaf(root->lchild); 
        Preorderleaf(root->rchild); 
    } 
} 
int LeafCount(BiTree &root)  //统计叶子节点的个数 
{ 
    int leaf; 
    if(root==NULL) 
    leaf=0; 
    else if(root->lchild==NULL&&root->rchild==NULL) 
    leaf=1; 
    else  
    leaf=LeafCount(root->lchild)+LeafCount(root->rchild); 
    return leaf; 
} 
int PostTreeDepth(BiTree &root)  //统计树的高度 
{ 
    int hl,hr,max; 
    if(root!=NULL) 
    { 
        hl=PostTreeDepth(root->lchild); 
        hr=PostTreeDepth(root->rchild); 
        max=Max(hl,hr); 
        return max+1; 
    } 
    else  
    return 0; 
} 
void dowork() 
{ 
    BiTree cam; 
    Create(cam); 
    Preorder(cam); 
    printf("\n"); 
    Inorder(cam); 
    printf("\n"); 
    Postorder(cam); 
    printf("\n"); 
    printf("叶子节点："); 
    Preorderleaf(cam); 
    printf("\n"); 
    printf("叶子节点的个数为:%d\n",LeafCount(cam)); 
    printf("树的深度为:%d\n",PostTreeDepth(cam)); 
} 
int main() 
{ 
    dowork(); 
    return 0; 
}