SGU 177. Square dfs 漂浮法倒序染色

177. Square

time limit per test: 2.5 sec.
memory limit per test: 65536 KB

input: standard
output: standard

You have given the square NxN on a checkered sheet. Size of each cell is 1x1, (1, 1) is leftmost top corner and (N, N) is rightmost bottom corner. 
Initially all cells are white. 
There are M repaintings inside of the square, where one repainting changes color of specified rectangle to some color (white or black). All sides of repainted rectangles are parallel to sides of square. 
You need to find amount of white cells after all repaintings.

Input

The first line of input consists of two numbers N and M (1<=N<=1000, 1<=M<=5000). Each of the next M lines consists of X1 Y1 X2 Y2 C, where (X1, Y1) and (X2, Y2) are indexes of opposite corners of the rectangular, and C is a symbol 'b' or 'w' ('b' means black color and 'w' - white) (1<=X1,X2,Y1,Y2<=N). All numbers in input are integer.

Output

Write amount of white cells after all repaintings.

Sample test(s)

Input

 

 

9 6 
2 2 4 6 b 
4 3 3 3 w 
6 2 8 6 b 
5 3 6 9 w 
8 3 9 9 w 
1 5 3 5 w

 

 

Output

 

 

63

 

這題跟USACO 3.1.4  Shaping Regions 基本一樣。。。

這題可以用線段樹矩陣切割的方式來做，當然也可以用dfs漂浮法倒序染色的方式來做。

什麽是漂浮法？

首先，我們對於所有的染色方式讀入，然後從後面往前面開始染色。

當一個塊已經被後面的染色方式染過色之後，不會繼續對它進行染色。

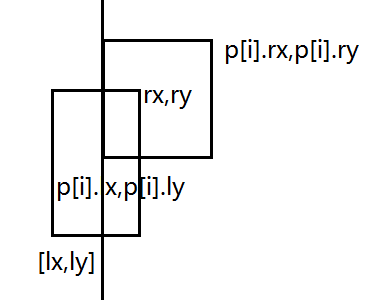
比如如下圖所示：當前需要染色的塊，假設為i-1，座標為{[lx,ly],[rx,ry]}，然後從第i塊開始往後面染色。所以我們只需要考慮第i-1塊沒有被第i塊覆蓋的地方進行染色即可。即遞歸下去對{[lx,ly],[p[i].lx-1,ry]}和對{[p[i].lx,ly],[rx,p[i].ry-1]}這兩個部份進行染色（注意這裡有些地方需要減一）。而{[p[i].lx,p[i].ly],[rx,ry]}被後面的覆蓋了，所以可以不用再對它進行染色。同理還有其他的相交情況，具體的看代碼

 

 

 

 

/*



題目：矩陣染色

分析：漂浮法染色。



*/

#include <set>

#include <map>

#include <cmath>

#include <queue>

#include <stack>

#include <string>

#include <vector>

#include <cstdio>

#include <cstring>

#include <iostream>

#include <algorithm>



using namespace std;



typedef long long ll;

typedef unsigned long long ull;



#define lx(x) (x<<1)

#define rx(x) (x<<1|1)

#define debug puts("here")

#define rep(i,n) for(int i=0;i<n;i++)

#define rep1(i,n) for(int i=1;i<=n;i++)

#define REP(i,a,b) for(int i=a;i<=b;i++)

#define foreach(i,vec) for(unsigned i=0;i<vec.size();i++)

#define pb push_back

#define RD(n) scanf("%d",&n)

#define RD2(x,y) scanf("%d%d",&x,&y)

#define RD3(x,y,z) scanf("%d%d%d",&x,&y,&z)

#define RD4(x,y,z,w) scanf("%d%d%d%d",&x,&y,&z,&w)



/******** program ********************/



const int MAXN = 5005;



int n,m,ans;



struct node{

    int lx,ly,rx,ry,col;

    void rd(){

        RD4(lx,ly,rx,ry);

        char op[2];

        scanf("%s",op);

        col = op[0]=='b';

        if(lx>rx)swap(lx,rx);

        if(ly>ry)swap(ly,ry);

    }

}p[MAXN];



void dfs(int lx,int ly,int rx,int ry,int col,int i){

    if(lx>rx||ly>ry)return; //不符合

    while(i<=m&&(lx>p[i].rx||ly>p[i].ry||rx<p[i].lx||ry<p[i].ly))

        i ++; // 兩個塊不相交

    if(i>m){ // 已經染完色

        if(col) ans += (rx-lx+1)*(ry-ly+1); // 更新黑色的塊

        return;

    }



    if( lx<p[i].lx ){

        dfs(lx,ly,p[i].lx-1,ry,col,i+1);

        lx = p[i].lx; // 更新

    }

    if( rx>p[i].rx ){

        dfs( p[i].rx+1,ly,rx,ry,col,i+1 );

        rx = p[i].rx;

    }

    if( ly<p[i].ly )

        dfs( lx,ly,rx,p[i].ly-1,col,i+1 );

    if( ry>p[i].ry )

        dfs( lx,p[i].ry+1,rx,ry,col,i+1 );

}



int main(){



#ifndef ONLINE_JUDGE

	freopen("sum.in","r",stdin);

	//freopen("sum.out","w",stdout);

#endif



    RD2(n,m);

    rep1(i,m)

        p[i].rd();

    for(int i=m;i;i--)

        dfs(p[i].lx,p[i].ly,p[i].rx,p[i].ry,p[i].col,i+1);

    cout<<n*n-ans<<endl;

    //cout<<ans<<endl;



	return 0;

}