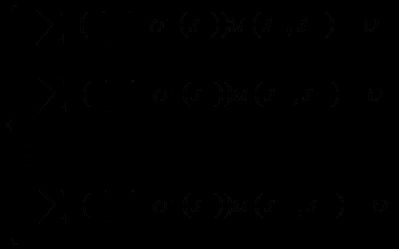博弈论——战略式博弈

图1 战略式博弈

1. 问题提出

囚徒困境（prisoner’ dilemma）_{——Tuncker 20世纪50年代}（纯战略）

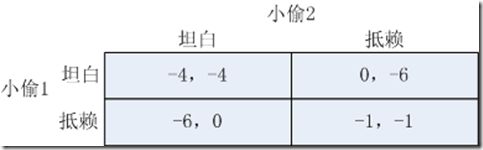
两个小偷作案后被警察抓住，分别 不同的屋子里审讯。在审讯之前，小偷从律师那里得知：如果两个人都坦白，将被各判刑4年；如果两个人都抵赖，将会因为证据不足而各判1年；如果其中一人坦白而另一人抵赖，坦白的将会得到宽大处理而被无罪释放，而抵赖的将重判，判刑6年。试问两个小偷将会如何选择？

纯战略：参与人在给定信息下只选择一种特定的战略（行动）。

猜硬币（混合战略）

两个参与人各握一枚硬币，双方同时选择是正面向上（记作O）还是背面向上（记作R），即他们的战略空间都是{O，R}。若两枚硬币是一致的（即全部背面向上或者全部正面向上），参与人2赢得参与人1的硬币；若两枚硬币不一致，则参与人1赢得参与人2的硬币。

混合战略：参与人在给定信息下以某种概率分布随机地选择不同的行动（战略空间上的概率分布）。解释了一个参与人对其他参与人所采取行动的不确定性。

在一个给定的n人战略式博弈中，对于任一参与人，设，则参与人i的一个混合战略为定义在战略集上的一个概率分布，其中表示参与人i选择战略的概率，即满足：且。

2. 问题描述——战略式博弈

战略式博弈（strategic form game）：也称标准式博弈，是一种相互作用的决策模型，这种模型假设每个参与人仅选择一次行动或行动计划（战略），并且这些选择是同时进行的。

适用：不需要考虑博弈过程的完全信息博弈问题(特别是完全信息静态博弈)

战略式博弈三要素：

1) 参与人集合

2) 每位参与人非空的战略集，即

3) 每位参与人定义在所有战略组合上的偏好关系或者效用函数

有限博弈：（参与人人数有限）且，（每个参与人的战略数有限），记为或

“囚徒困境”博弈战略式描述：

表1 “囚徒困境”战略式描述

“猜硬币”战略式描述：

表2 “猜硬币”战略式描述

3. 问题的解——Nash均衡（纯战略）、混合战略Nash均衡（混合战略）

1) 重复剔除劣战略行为（化简原博弈问题）

在n人博弈中，如果对于参与人i，存在战略，对，有，则称战略为参与人i的劣战略（严格劣战略），或者战略相对于占优；有，且，使得，则称战略为参与人i的弱劣战略。

参与人i将会把从中剔除掉，直接从战略集中选择自己的战略。------------------------->，其中

注：如果每次剔除的是严格劣战略，均衡结果与剔除顺序无关；如果剔除的是弱劣战略，均衡结果可能与剔除顺序有关。

2) 纯战略——Nash均衡（Nash Equilibrium）_{——John Nash 20世纪50年代}

在一个给定的n人战略式博弈中，战略组合是一个Nash均衡，当且仅当，时，有或者，。

3) 混合战略——混合战略Nash均衡

在一个给定的n人战略式博弈中，混合战略组合为一个Nash均衡，当且仅当，，有。

支撑求解法

支撑（记为）是指参与人按照选择战略时，纯战略组合中以大于0的概率出现的所有纯战略组合的集合，即

有限n人战略式博弈的支撑求解法：

1) 构造出所有的混合战略均衡的支撑。

2) 对于每个给定的支撑，求解如下方程组。

3) 验证方程组的解。

a) 解都大于0。即

b) 不存在一个不属于支集的战略，给定其他参与人的战略，参与人i采用所得到的期望效用大于采用支集中战略的期望效用。即但，

规划求解法

将求解博弈的混合战略Nash均衡转换为对一个规划问题进行求解。

有限n人战略式博弈的规划求解法：

Wilson奇数定理（oddness theorem）：几乎所有的有限战略式博弈都有有限奇数个Nash均衡。

 

参考文献：

[1] 罗云峰. 博弈论教程. 北京: 清华大学出版社, 北京交通大学出版社, 2007.