多视角学习-协同训练

一．半监督学习

      在传统的有监督学习中，我们通过训练大量有标记数据得到一个强学习器，然后预测一个未知样例。而现实生活中，通常数据集中大量数据是无标记的，只有很少一部分是有标记的。比如在电子商务系统中，我们需要推荐用户感兴趣的商品，然而只有很少的用户会主动标记他们感兴趣的商品，系统中还存在着大量其他的商品，它们都可作为未标记示例来使用。我们的目标就是利用这些大量的、廉价的无标记数据帮助我们得到更好的训练模型。

      贝叶斯公式P(Ci|x)=ΣP(x|Ci)P(Ci)/P(x)，表明我们可以将先验概率P(Ci)转换为后验概率P(Ci|x)。P(Ci|x)代表在输入示例的特征向量x的条件下该示例类别属于Ci 的概率。我们能够从标记数据中计算出P(x|Ci)和P(Ci)，大量的无标记数据则有助于得到更接近于真值的p(x)。由贝叶斯公式可以看出p(x)能够影响到P(Ci|x)的值，也就是说大量的无标记数据是有助于分类器学习的。

 

二．协同训练

      协同训练是一种多视角学习方法，与我们熟知的单视角不同。比如在网页分类的问题中，网页拥有两个独立的视图即链接和网页内容。当数据充分时，在具有这种特征的数据集的任何一个视图上均可以利用一定的机器学习算法训练出一个强分类器。因为无论是链接还是网页内容都能独立完备地唯一确定一个网页。但是在这里，大量数据都是无标记的，无法训练出一个强泛化能力的分类器，怎么办呢？协同训练应运而生！

 

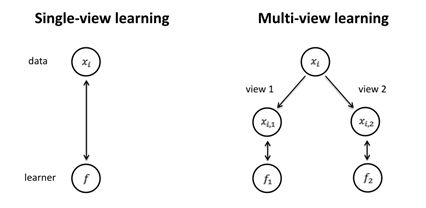
      假设数据集属性有两个充分冗余的视图view1和view2，设为X1和X2，则一个示例就可以表示为(x1, x2)，其中x1是x在X1视图中的特征向量，x2则是x在X2视图中的特征向量。假设f是在示例空间X中的目标函数，若x的标记为l则应有f(x) = f1(x1) = f2(x2) = l。A. Blum和T. Mitchell定义了所谓的“相容性”，即对X上的某个分布D，C1和C2分别是定义在X1和X2上的概念类，如果D对满足f1(x) ≠ f2(x2) 的示例 (x1, x2) 指派零概率，则称目标函数f = (f1, f2) ∈ C1 × C2与D“相容”。

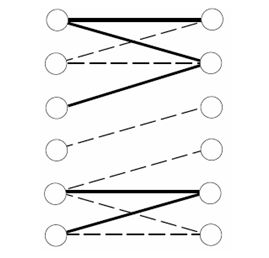
      这样，就有可能利用未标记示例来辅助探查哪些目标概念是相容的，而该信息有助于减少学习算法所需的有标记示例数。下图左边的每个结点对应了X1中的一个特征向量，右边的每个结点对应了X2中的一个特征向量，当且仅当示例(x1, x2)在分布D下以非零概率存在时，结点x1和x2之间才存在边，这些边在图中已经用线条标示出来，其中用实边标示的边对应了已经观察到的未标记示例。在这一表示下，C中与D相容的概念就对应了在图中连通成分之间没有交叉线的划分。显然，属于同一连通成分的示例必然属于同样的类别，而未标记示例可以帮助学习算法了解图中的连通性（了解分布D），因此，通过利用未标记示例，学习算法可以使用较少的有标记示例达到原来需要更多的有标记示例才能达到的效果。

标准协同训练算法的步骤为：

输入：标记数据集L，未标记数据集U。

• 用L1训练视图X1上的分类器f1，用L2训练视图X2上的分类器f2；
• 用f1和f2分别对未标记数据U进行分类；
• 把f1对U的分类结果中，前k个最置信的数据（正例p个反例n个）及其分类结果加入L2；把f2对U的分类结果中，前k个最置信的数据及其分类结果加入L1；把这2（p+n）个数据从U中移除；
• 重复上述过程，直到U为空集。

输出：分类器f1和f2。

注： f1和f2可以是同一种分类器也可以不是同一种分类器。

 

三．参考和其他学习资料

[1].Combining Labeled and Unlabeled Data with Co-Training

[2].半监督学习中的协同训练风范

[3].A Co-Regularization Approach to Semi-supervised Learning with Multiple Views

[4].When Does Co-Training Work in Real Data?

[5].Semi-Supervised Learning with Multiple Views 

 

转载请注明出处：http://www.cnblogs.com/Rosanna/p/3638051.html