BZOJ 1101: [POI2007]Zap

---

题目

---

 

1101: [POI2007]Zap

Time Limit: 10 Sec   Memory Limit: 162 MB

Description

FGD正在破解一段密码，他需要回答很多类似的问题：对于给定的整数a,b和d，有多少正整数对x,y，满足x<=a，y<=b，并且gcd(x,y)=d。作为FGD的同学，FGD希望得到你的帮助。

Input

第一行包含一个正整数n，表示一共有n组询问。（1<=n<= 50000）接下来n行，每行表示一个询问，每行三个正整数，分别为a,b,d。（1<=d<=a,b<=50000）

Output

对于每组询问，输出到输出文件zap.out一个正整数，表示满足条件的整数对数。

Sample Input

2
4 5 2
6 4 3

Sample Output

3
2

HINT

 

对于第一组询问，满足条件的整数对有(2,2)，（2,4），（4，2）。对于第二组询问，满足条件的整数对有（6,3），（3,3）。

 

---

题解

---

由数论推知->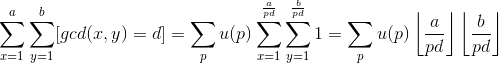

且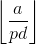只会有种取值，所以我们暴力就好了！

---

 

代码

---

 

/*Author:WNJXYK*/

#include<cstdio>

#include<iostream>

#include<cstring>

#include<string>

#include<algorithm>

#include<queue>

#include<set>

#include<map>

using namespace std;



#define LL long long

#define Inf 2147483647

#define InfL 10000000000LL



inline void swap(int &x,int &y){int tmp=x;x=y;y=tmp;}

inline void swap(LL &x,LL &y){LL tmp=x;x=y;y=tmp;}

inline int remin(int a,int b){if (a<b) return a;return b;}

inline int remax(int a,int b){if (a>b) return a;return b;}

inline LL remin(LL a,LL b){if (a<b) return a;return b;}

inline LL remax(LL a,LL b){if (a>b) return a;return b;}

inline void read(int &x){x=0;int f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}x=x*f;}

inline void read(LL &x){x=0;LL f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}x=x*f;}

inline void read(int &x,int &y){read(x);read(y);}

inline void read(LL &x,LL &y){read(x);read(y);}

inline void read(int &x,int &y,int &z){read(x,y);read(z);}

inline void read(int &x,int &y,int &n,int &m){read(x,y);read(n,m);}

inline void read(LL &x,LL &y,LL &z){read(x,y);read(z);}

inline void read(LL &x,LL &y,LL &n,LL &m){read(x,y);read(n,m);}



const int Maxn=50000;

LL miu[Maxn+10];

inline void getMiu(){

	for (int i=1;i<=Maxn;i++){

		int target=i==1?1:0;

		int delta=target-miu[i];

		miu[i]=delta;

		for (int j=i+i;j<=Maxn;j+=i) miu[j]+=delta;

	}	

	for (int i=2;i<=Maxn;i++) miu[i]+=miu[i-1]; 

}



inline LL getAns(int n,int m){

	if (n>m) swap(n,m);

	LL Ans=0;

	int pos;

	for (int i=1;i<=n;i=pos+1){

		pos=remin(n/(n/i),m/(m/i));

		Ans+=(miu[pos]-miu[i-1])*(n/i)*(m/i);

	} 

	return Ans;

}



int T;

LL a,b,d;

int main(){

	read(T);

	getMiu();

	for (;T--;){

		read(a,b,d);

		printf("%lld\n",getAns(a/d,b/d));

	}

	

	return 0;

}