隐马尔科夫模型及Viterbi算法的应用

作者：jostree 转载请注明出处 http://www.cnblogs.com/jostree/p/4335810.html

一个例子：

韦小宝使用骰子进行游戏，他有两种骰子一种正常的骰子，还有一种不均匀的骰子，来进行出千。

开始游戏时他有2/5的概率出千。

对于正常的骰子A，每个点出现的概率都是1/6.

对于不均匀的骰子B，5，6两种出现的概率为3/10，其余为1/10.

出千的随机规律如下图所示：

 

 

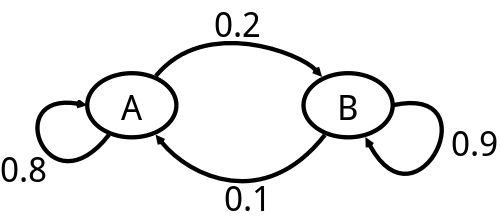
我们观测到的投掷结果为：ob={1，3，4，5，5，6，6，3，2，6}

请判断韦小宝什么时候出千了？

我们可以这样建模$x_i$表示第$i$次投掷的骰子的种类，$y_i$表示第$i$次投掷出的点数，$\lambda$表示各个概率参数。

那么第$t$次使用第$i$种骰子投掷的概率$\delta_t(i)$等于

\begin{equation} \delta_t(i)=\max_{x_1,\dots,x_{t-1}}P(x_1,\dots,x_{t-1},x_t=i,y_1,\dots,y_t|\lambda) \end{equation}

其实$\delta_{t+1}(i)$可以由$\delta_t(i)$推倒得出：

\begin{eqnarray} \delta_{t+1}(i) &=& \max_{x_1,\dots,x_{t}}P(x_1,\dots,x_{t},x_{t+1}=i,y_1,\dots,y_{t+1}|\lambda)\\ &=& \max_j \delta_t(j)\alpha_{ji}\beta_i(y_{t+1})\end{eqnarray}

其中$\alpha_{ji}$表示从第$j$个骰子转移到第$i$个骰子的概率。

$\beta_i(y_{t+1})$表示使用第i个骰子投出点$y_{t+1}$的概率。

从而可以使用上述利用动态规划算法进行逐次递推计算。

得到的结果为：

 

t	$y_t$	$\delta_t(A)$	$\Psi_t(A)$	$\delta_t(B)$	$\Psi_t(B)$
1	1	0.1	A	0.04	A
2	3	0.0133333	A	0.0036	B
3	4	0.00177778	A	0.000324	B
4	5	0.000237037	A	0.000106667	A
5	5	3.16049e-05	A	2.88e-05	B
6	6	4.21399e-06	A	7.776e-06	B
7	6	5.61866e-07	A	2.09952e-06	B
8	3	7.49154e-08	A	1.88957e-07	B
9	2	9.98872e-09	A	1.70061e-08	B
10	6	1.33183e-09	A	4.59165e-09	B

因为最后一步$\delta_t(B)$的值大于$\delta_t(A)$，所以一次使用B骰子的概率最大，从而一直向上回溯，得到的使用骰子的序列为：AAABBBBBBB

代码如下所示：

 1 #include <stdlib.h>

 2 #include <stdio.h>

 3 #include <string.h>

 4 #include <string>

 5 #include <iostream>

 6 using namespace std;

 7 double initP[2] = {0.6, 0.4};//骰子A，B的初始概率

 8 double transferMatrix[2][2] = {{0.8, 0.2}, {0.1, 0.9}};//骰子之间的转移概率

 9 double EmissionP[2][6]={{1/6.0, 1/6.0, 1/6.0, 1/6.0, 1/6.0, 1/6.0},//骰子A的发射概率

10                         {0.1, 0.1, 0.1, 0.1, 0.3, 0.3}};//骰子B的发射概率

11 double dp[10][2];//dp[i][j]第i步时，使用第j个骰子的最大概率

12 double dpS[10][2];//dpS[i][j]第i步时，使用第j个骰子，得到的最大概率时，使用的骰子种类, 0->A, 1->B

13 int ob[10] = {1, 3, 4, 5, 5, 6, 6, 3, 2, 6};//观测点数

14 bool diceArray[10];//预测骰子使用序列

15 void Viterbi()

16 {

17     memset(dp,0,sizeof(dp));

18     memset(dpS,0,sizeof(dpS));

19     memset(diceArray,0,sizeof(diceArray));

20     dp[0][0] = initP[0]* EmissionP[0][ob[0]-1];

21     dp[0][1] = initP[1]* EmissionP[1][ob[0]-1];

22     for( int i = 1 ; i < 10 ; i++ )//投掷次数

23     {

24         for( int j = 0 ; j < 2 ; j++ )//当前状态

25         {

26             for( int k = 0 ; k < 2 ; k++ )//上一个状态

27             {

28                 double tempP = dp[i-1][k] * transferMatrix[k][j] * EmissionP[j][ob[i]-1] ;

29                 if( dp[i][j] < tempP )

30                 {

31                     dp[i][j] = tempP;

32                     dpS[i][j] = k;

33                 }

34             }

35         }

36     }

37     int maxState = 0;

38     if( dpS[9][0] < dpS[9][1] )

39     {

40         maxState = 1;

41     }

42     for( int i = 9 ; i >=0 ; i-- )

43     {

44         diceArray[i] = maxState; 

45         maxState = dpS[i][maxState];

46     }

47 }

48 int main(int argc, char *argv[])

49 {

50     Viterbi();

51     cout<<"每步每个状态下的概率和骰子种类:"<<endl;

52     for( int i = 0 ; i < 10 ; i++ )

53     {

54         for( int j = 0 ; j < 2 ; j++ )

55         {

56             cout<<dp[i][j]<<" "<<dpS[i][j]<<"    ";

57         }

58         cout<<endl;

59     }

60     cout<<"预测骰子种类，0->A, 1->B : "<<endl;

61     for( int i = 0 ; i < 10 ; i++ )

62     {

63         cout<<diceArray[i]<<" ";

64     }

65     cout<<endl;

66 }

67 /* result:

68 每步每个状态下的概率和骰子种类:

69 0.1 0    0.04 0    

70 0.0133333 0    0.0036 1    

71 0.00177778 0    0.000324 1    

72 0.000237037 0    0.000106667 0    

73 3.16049e-05 0    2.88e-05 1    

74 4.21399e-06 0    7.776e-06 1    

75 5.61866e-07 0    2.09952e-06 1    

76 7.49154e-08 0    1.88957e-07 1    

77 9.98872e-09 0    1.70061e-08 1    

78 1.33183e-09 0    4.59165e-09 1    

79 预测骰子种类，0->A, 1->B : 

80 0 0 0 1 1 1 1 1 1 1 

81 */

View Code