九大排序算法Demo
1. 冒泡排序
冒泡排序（Bubble Sort）是一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
1 int[] array = {5, 4, 3, 2, 1}; 2 3 boolean isChanged = false; 4 for (int i = 0; i < array.length; i++) { 5 isChanged = false; 6 7 for (int j = 0; j < (array.length - i - 1); j++) { 8 if (array[j] > array[j + 1]) { 9 int temp = array[j]; 10 array[j] = array[j + 1]; 11 array[j + 1] = temp; 12 13 isChanged = true; 14 } 15 } 16 17 if (!isChanged) { 18 break; 19 } 20 }
四次遍历
4 3 2 1 5
3 2 1 4 5
2 1 3 4 5
1 2 3 4 5
最大比较次数： n(n-1)/2 时间复杂度(最坏情况)： O(2^n)
最小比较次数： n-1 时间复杂度(最好情况): O(n)
2. 快速排序
是由东尼·霍尔所发展的一种排序算法 基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。
public static void main(String[] args) { // 快速排序 int[] array = {8, 2, 4 ,7 ,1 ,9 ,3 ,6, 5}; sortMe(array, 0, array.length-1); for (int i = 0; i < array.length; i++) { System.out.print(array[i] + ","); } } public static void sortMe(int[] array, int low,int high){ if(low < high){ // 将list数组进行一分为二 int middle = getMiddle(array, low, high); // 对低字表进行递归排序 sortMe(array, low, middle-1); // 对高字表进行递归排序 sortMe(array, middle+1, high); } } public static int getMiddle(int[] array, int low,int high){ // 数组的第一个作为中轴 int temp = array[low]; while(low < high){ while(low < high && array[high] > temp){ high--; } // 比中轴小的记录移到低端 array[low] = array[high]; while(low < high && array[low] <= temp){ low++; } // 比中轴大的记录移到高端 array[high] = array[low]; } array[low] = temp; //中轴记录到尾 return low; //返回中轴的位置 }
3. 直接插入排序
1、算法概念。
2、算法思想。
假设待排序的记录存放在数组R[1..n]中。初始时，R[1]自成1个有序区，无序区为R[2..n]。从i=2起直至i=n为止，依次将R[i]插入当前的有序区R[1..i-1]中，生成含n个记录的有序区。
3、实现思路。
①用一个临时变量temp存储第i个元素（i>=1，下标从0开始）。
②比较R[i] 和R[i+1]，如果R[i+1].compareTo(R[i])<0,则R[i+1] = R[i],即比R[i+1]的集合元素依次往右移动一个单位。
③将temp的值赋给R[i].
public static void main(String[] args) {
// 直接插入排序
int[] array = {8, 2, 4 ,7 ,1 ,9 ,3 ,6, 5};
insertSort(array);
for (int i = 0; i < array.length; i++) {
System.out.print(array[i] + ",");
}
}
public static void insertSort(int[] data)
{
int length = data.length;
for (int i = 1; i < length; i++)
{
int tmp = data[i];
if (tmp < data[i - 1])
{
int j = i - 1;
for (; j >= 0 && data[j] > tmp; j--)
{
data[j + 1] = data[j];
}
data[j + 1] = tmp;
}
}
}
4. 堆排序
堆排序的思想
利用大顶堆(小顶堆)堆顶记录的是最大关键字(最小关键字)这一特性，使得每次从无序中选择最大记录(最小记录)变得简单。
其基本思想为(大顶堆)：
1)将初始待排序关键字序列(R1,R2....Rn)构建成大顶堆，此堆为初始的无序区；
2)将堆顶元素R[1]与最后一个元素R[n]交换，此时得到新的无序区(R1,R2,......Rn-1)和新的有序区(Rn),且满足R[1,2...n-1]<=R[n];
3)由于交换后新的堆顶R[1]可能违反堆的性质，因此需要对当前无序区(R1,R2,......Rn-1)调整为新堆，然后再次将R[1]与无序区最后一个元素交换，得到新的无序区(R1,R2....Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1，则整个排序过程完成。
操作过程如下：
1)初始化堆：将R[1..n]构造为堆；
2)将当前无序区的堆顶元素R[1]同该区间的最后一个记录交换，然后将新的无序区调整为新的堆。
因此对于堆排序，最重要的两个操作就是构造初始堆和调整堆，其实构造初始堆事实上也是调整堆的过程，只不过构造初始堆是对所有的非叶节点都进行调整。
下面举例说明：
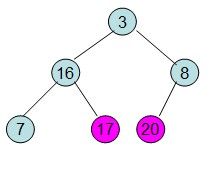
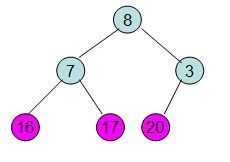
给定一个整形数组a[]={16,7,3,20,17,8}，对其进行堆排序。
首先根据该数组元素构建一个完全二叉树，得到
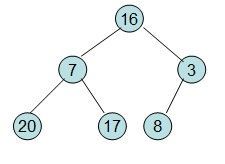
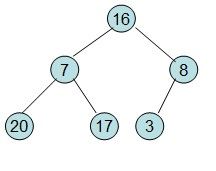
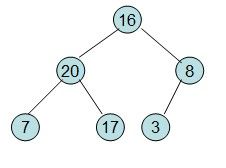
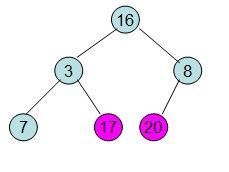
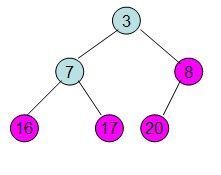
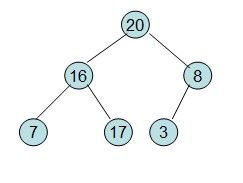20和16交换后导致16不满足堆的性质，因此需重新调整
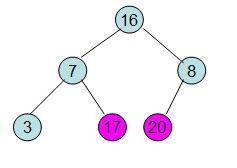
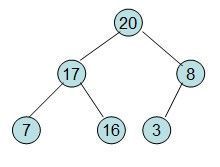这样就得到了初始堆。
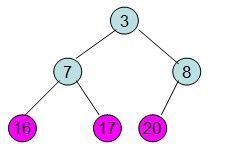
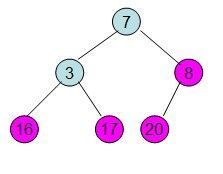
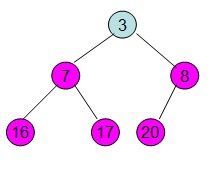
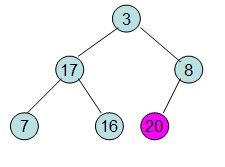此时3位于堆顶不满堆的性质，则需调整继续调整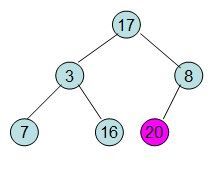
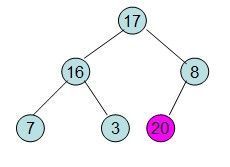
private static int[] sort = new int[] {
1, 0, 10, 20, 3, 5, 6, 4, 9, 8, 12,
17, 34, 11
};
public static void main(String[] args) {
buildMaxHeapify(sort);
heapSort(sort);
print(sort);
}
private static void buildMaxHeapify(int[] data) {
// 没有子节点的才需要创建最大堆，从最后一个的父节点开始
int startIndex = getParentIndex(data.length - 1);
// 从尾端开始创建最大堆，每次都是正确的堆
for (int i = startIndex; i >= 0; i--) {
maxHeapify(data, data.length, i);
}
}
/**
* 创建最大堆
*
* @paramdata
* @paramheapSize需要创建最大堆的大小，一般在sort的时候用到，因为最多值放在末尾，末尾就不再归入最大堆了
* @paramindex当前需要创建最大堆的位置
*/
private static void maxHeapify(int[] data, int heapSize, int index) {
// 当前点与左右子节点比较
int left = getChildLeftIndex(index);
int right = getChildRightIndex(index);
int largest = index;
if (left < heapSize && data[index] < data[left]) {
largest = left;
}
if (right < heapSize && data[largest] < data[right]) {
largest = right;
}
// 得到最大值后可能需要交换，如果交换了，其子节点可能就不是最大堆了，需要重新调整
if (largest != index) {
int temp = data[index];
data[index] = data[largest];
data[largest] = temp;
maxHeapify(data, heapSize, largest);
}
}
/**
* 排序，最大值放在末尾，data虽然是最大堆，在排序后就成了递增的
*
* @paramdata
*/
private static void heapSort(int[] data) {
// 末尾与头交换，交换后调整最大堆
for (int i = data.length - 1; i > 0; i--) {
int temp = data[0];
data[0] = data[i];
data[i] = temp;
maxHeapify(data, i, 0);
}
}
/**
* 父节点位置
*
* @paramcurrent
* @return
*/
private static int getParentIndex(int current) {
return (current - 1) >> 1;
}
/**
* 左子节点position注意括号，加法优先级更高
*
* @paramcurrent
* @return
*/
private static int getChildLeftIndex(int current) {
return (current << 1) + 1;
}
/**
* 右子节点position
*
* @paramcurrent
* @return
*/
private static int getChildRightIndex(int current) {
return (current << 1) + 2;
}
private static void print(int[] data) {
int pre = -2;
for (int i = 0; i < data.length; i++) {
if (pre < (int) getLog(i + 1)) {
pre = (int) getLog(i + 1);
System.out.println();
}
System.out.print(data[i] + "|");
}
}
/**
* 以2为底的对数
*
* @paramparam
* @return
*/
private static double getLog(double param) {
return Math.log(param) / Math.log(2);
}
5. 归并排序