HDU 4331 Image Recognition

树状数组+扫描线

官方题解：

本题题目大意在一个01方阵中找出四条边全都是1的正方形的个数，对于正方形内部则没有要求。
一个直观的想法是首先用N^2的时间预处理出每一个是1的点向上下左右四个方向能够延伸的1的最大长度，记为四个数组l, r, u, d。然后我们观察到正方形有一个特征是同一对角线上的两个顶点在原方阵的同一条对角线上。于是我们可以想到枚举原来方阵的每条对角线，然后我们对于每条对角线枚举对角线上所有是1的点i，那么我们可以发现可能和i构成正方形的点应该在该对角线的 [i, i + min(r[i], d[i]) – 1] 闭区间内， 而在这个区间内的点 j 只要满足 j – i + 1 <= min(l[j], u[j]) 也就是满足j – min(l[j], u[j]) + 1 <= i，这样的 (i, j) 就能构成一个正方形。也就是说对于每条对角线，我们可以构造一个数组 a, 使得a[i] = i – min(l[i], u[i]) + 1
然后对这个数组有若干次查询，每次查询的是区间 [i, i + min(r[i], d[i]) – 1]内有多少个数满足 a[j] <= i，所有这些问题答案的和就是该问题的结果。对于这个问题，我们可以通过离线算法，先保存所有查询的区间端点，并对所有端点排序。然后使用扫描线算法，如果扫描到的是第i次查询的左端点，就让当前结果减去当前扫描过的数中 <= i的个数，如果扫描到的是第i次查询的右端点，则让当前结果加上当前扫描过的数中 <= i的个数，最后所有结果相加即可。
维护当前数出现的个数可以使用树状数组。这样对于每条对角线求结果的复杂度为O(nlogn)，算法总的复杂度为O(n^2logn)。

 

 

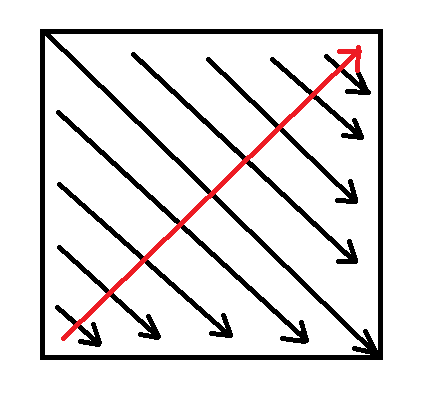
这个我唯一没搞明白的是对角线是怎么枚举的，对于为啥分了上三角和下三角费解了很久。后来才明白是以这样的顺序枚举的：

 

  1 #include <cstdio>

  2 #include <cstring>

  3 #include <cstdlib>

  4 #include <algorithm>

  5 

  6 using namespace std;

  7 

  8 const int MAXN = 1010;

  9 

 10 struct node

 11 {

 12     int id;

 13     int x;

 14     bool left;

 15 };

 16 

 17 int map[MAXN][MAXN];

 18 int up[MAXN][MAXN], down[MAXN][MAXN], left[MAXN][MAXN], right[MAXN][MAXN];

 19 int a[ MAXN << 1 ];

 20 int C[ MAXN << 1 ];

 21 node D[ MAXN << 1 ];

 22 int N;

 23 

 24 bool cmp( node a, node b )

 25 {

 26     if ( a.x == b.x ) return a.left;

 27     return a.x < b.x;

 28 }

 29 

 30 int lowbit( int x )

 31 {

 32     return x & (-x);

 33 }

 34 

 35 int sum( int x )

 36 {

 37     int ret = 0;

 38     while ( x > 0 )

 39     {

 40         ret += C[x];

 41         x -= lowbit(x);

 42     }

 43     return ret;

 44 }

 45 

 46 void add( int x )

 47 {

 48     while ( x < ( MAXN << 1 ) )

 49     {

 50         C[x] += 1;

 51         x += lowbit(x);

 52     }

 53     return;

 54 }

 55 

 56 void init()

 57 {

 58     memset( up,    0, sizeof(up) );

 59     memset( down,  0, sizeof(down) );

 60     memset( left,  0, sizeof(left) );

 61     memset( right, 0, sizeof(right) );

 62     for ( int i = 1; i <= N; ++i )

 63     for ( int j = 1; j <= N; ++j )

 64     {

 65         scanf( "%d", &map[i][j] );

 66         if ( map[i][j] )

 67         {

 68             left[i][j] = left[i][j - 1] + 1;

 69             up[i][j] = up[i - 1][j] + 1;

 70         }

 71     }

 72 

 73     for ( int i = N; i > 0; --i )

 74     for ( int j = N; j > 0; --j )

 75     {

 76         if ( map[i][j] )

 77         {

 78             down[i][j] = down[i + 1][j] + 1;

 79             right[i][j] = right[i][j + 1] + 1;

 80         }

 81     }

 82 

 83     return;

 84 }

 85 

 86 int query( int m )

 87 {

 88     int ans = 0;

 89     memset( C, 0, sizeof(C) );

 90     sort( D, D + m, cmp );

 91     for ( int i = 0; i < m; ++i )

 92     {

 93         if( D[i].left )

 94         {

 95             ans -= sum( D[i].id );

 96             add( a[ D[i].x ] );

 97         }

 98         else ans += sum( D[i].id );

 99     }

100 

101     return ans;

102 }

103 

104 int solved()

105 {

106     int ans = 0;

107     for ( int i = N; i > 0; --i )

108     {

109         int cnt = 0;

110         for ( int j = 1; j <= N - i + 1; ++j )

111         {

112             int x = i + j - 1;

113             int y = j;

114             //printf( "%d %d\n", x, y );

115             if ( map[x][y] )

116             {

117                 D[cnt].id = y;

118                 D[cnt].left = true;

119                 D[cnt].x = y;

120                 a[y] = y - min( up[x][y], left[x][y] ) + 1;

121                 ++cnt;

122 

123                 D[cnt].id = y;

124                 D[cnt].left = false;

125                 D[cnt].x = y + min( right[x][y], down[x][y] ) - 1;

126                 ++cnt;

127             }

128         }

129         //puts("");

130         ans += query( cnt );

131     }

132 

133     for ( int i = N - 1; i > 0; --i )

134     {

135         int cnt = 0;

136         for ( int j = 1; j <= i; ++j )

137         {

138             int x = j;

139             int y = j + N - i;

140             //printf("%d %d\n", x, y );

141             if ( map[x][y] )

142             {

143                 a[y] = y - min( left[x][y], up[x][y] ) + 1;

144                 D[cnt].id = y;

145                 D[cnt].left = true;

146                 D[cnt].x = y;

147                 ++cnt;

148 

149                 D[cnt].id = y;

150                 D[cnt].left = false;

151                 D[cnt].x = y + min( down[x][y], right[x][y] ) - 1;

152                 ++cnt;

153             }

154         }

155         //puts("");

156         ans += query( cnt );

157     }

158 

159     return ans;

160 }

161 

162 int main()

163 {

164     int T;

165     int cas = 0;

166     scanf( "%d", &T );

167     while ( T-- )

168     {

169         scanf( "%d", &N );

170         init();

171         printf( "Case %d: %d\n", ++cas, solved() );

172     }

173     return 0;

174 }

思路很巧的一题