透过表象看本质!?之三——Kalman滤波
数据拟合能够估计出数据变化的趋势,另外一个同等重要的应用是如何利用这一趋势,预测下一时刻数据可能的值。通俗点儿说,你观察苍蝇(蚊子,蜜蜂)飞了几秒,你也许会想“它下一个时刻可能在哪儿”,“呈现出什么样的状态”诸如此类的问题。预知未来这档子事儿对我们有一种不可抗拒的吸引力。别看我们预测的未来很近,但这对于实际应用有很大的帮助。比如减小解空间的范围,便于搜索。对于搜索问题,预测可以看成是对从当前状态到目标状态的启发评价函数。好吧,我承认我陷得太深了,都是复习人工智能搞得。扯得有点儿远了,继续说我们的主题,预测。
古人每遇到重大活动,都会卜上一卦。念几句咒语,抽个签,看看签释,心里大概对所问之事有了个谱儿。再比如,这几天你的左眼皮一直在跳,你想知道这是为什么,意味着什么。你跑去算了一卦。抽签的时候,你心里默念着是不是要捡到钱了等等,结果抽了一个上上签,说你要遇到好事儿。“这几天眼皮跳”是你的观察数据。“你想知道未来会发生什么”是我们想要预测的东西。抽签的时候你心里默念的话,签儿,签上的符号和某些事件的对应关系,这些都是预测的算法。虽然占卜的过程包含了观察,有预测算法,有预测结果,同时也有结果的方差范围等等。但是我们说这种预测是不科学的,因为预测算法不科学,因果关系不见得成立等等。那有没有科学的预测呢,让我们进入今天的话题,Kalman滤波。
假设这样一个场景,A先生使用遥控器控制一架四轴直升飞机F在一个空旷的场地上飞行。直升飞机F上有一个GPS模块,通过无线发射模块实时的将直升飞机F的位置发给计算终端C。B先生在终端C上运行一个“打”直升飞机F的程序D。程序D根据终端C接收的GPS数据,指导一个虚拟的导弹E去跟踪直升飞机F,并试图将F“击落”。
A先生控制的直升飞机F飞行轨迹多变,很难被跟踪。同时,终端接收的GPS数据中还有噪声。B先生引导的导弹E燃料有限,因此不能长时间、频繁地机动。因此,B先生希望程序D要尽可能准的估计出F的位置,尽可能少机动,跟踪F并将其击落。
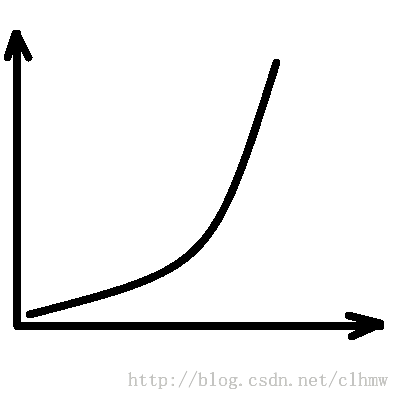
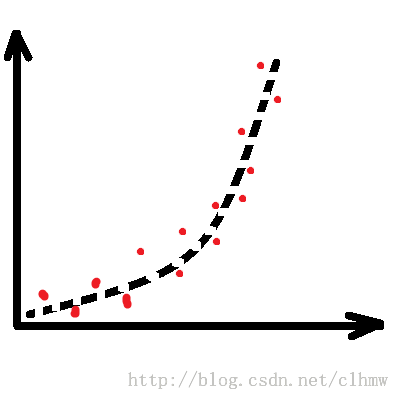
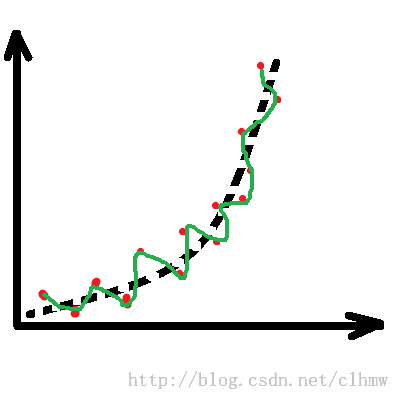
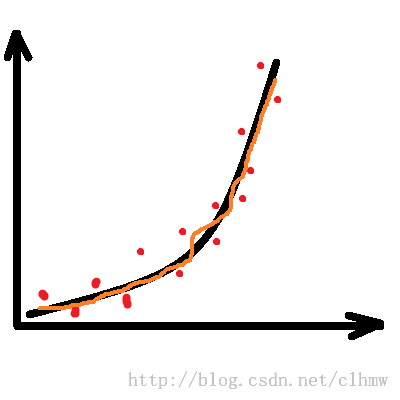
假如,A先生控制F急速攀升,如图1a。D得到的数据如图1b中的红色点。如果不进行预测,直接根据GPS数据控制E机动,E的运动轨迹如图1c,绿色的轨迹线。E很可能因燃料不足提前爆炸,而没有击中F。B先生很希望D能够根据GPS数据计算出如图1d所示的轨迹(橙色的轨迹线),来引导E去追踪F。
a b c d
图1 a、被观测对象实际的运动轨迹;b、我们观测到的被观测对象的运动轨迹;
c、如果不滤波的话,预测的轨迹;d、滤波后的预测轨迹。
假如A先生很狡猾,他控制F飞行,其飞行轨迹如图2所示。B先生深感压力巨大,如何才能有效的跟踪F,并将其击落呢。
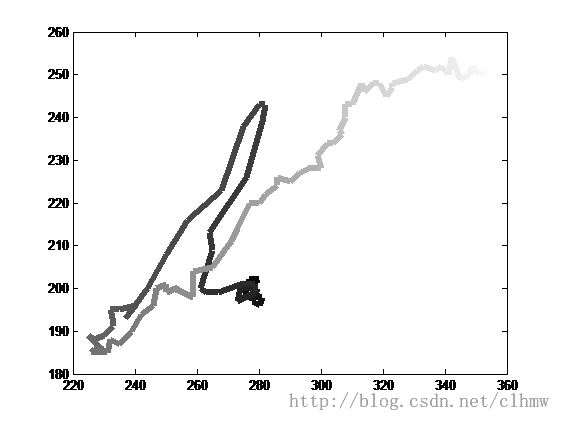
图2 A先生控制的直升飞机F可能飞出的轨迹(终端C得到的GPS数据)。
颜色越深,获取数据的时间越早;反之,颜色越浅,获取时间越晚。
程序D根据终端C提供的GPS数据,估计F的位置(x,y),时间t的采样记为。使用前t个时刻的采样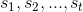 ,估计,使得该估计满足,
,估计,使得该估计满足,
(1)
(2)
其中,为范数。公式(1)是对历史数据的平滑(smooth,filter),公式(2)是对未来数据的预测(predict)。求解的过程是数据模型的更新。正如绪论中讨论的那样,数据模型可以形式化为,
其中s为观测直接得到的数据,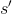 为观测数据的一阶微分或者偏微分,
为观测数据的一阶微分或者偏微分,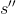 为二阶微分或者偏微分,省略的部分为更高阶的微分或者偏微分。假如模型的复杂度函数h和模型涉及的数据的阶数相关,阶数越小复杂度越小,阶数越高复杂度越高。估计需要满足的第三个公式是
为二阶微分或者偏微分,省略的部分为更高阶的微分或者偏微分。假如模型的复杂度函数h和模型涉及的数据的阶数相关,阶数越小复杂度越小,阶数越高复杂度越高。估计需要满足的第三个公式是
(3)
模型的复杂度控制就是正则化。
B将D指导E跟踪F轨迹这一问题抽象为这样一个模型,其中涉及观察变量和状态变量。观察变量是终端C得到的GPS数据,状态变量是程序D用于估计F位置的。Ft-1是状态转移矩阵,描述F的运动模型。Gt-1是控制矩阵,是外控制变量。Ht是观测矩阵,描述观测和状态之间的关系。Wt-1和Vt是高斯白噪声,covariance分别是Q和R,假设其不随状态变量变化。
(4)
(5)
Ft和Ht的如何确定的呢?我们首先插入一段广告。对于一个具有n阶导数的函数f,其在x处的泰勒展开为
(6)
忽略2阶以上的项,取x=t,x0=t-1,则上式可以写成
(7)
对上式分别求1阶和2阶导数有
(8)
(9)
用矩阵的形式重写公式(7)如下
(10)
对于离散模型的,微分用差分近似表示,式(8)(9)改写为
(11)
(12)
(13)
式(13)给出了要估计的函数、导数与观测数据之间的关系。
广告时间结束,言归正传Ft描述的是状态之间的关系。该关系受到运动学的基本关系式的约束。牛顿运动学定律可以使用式(10)表示。
如果,我们想实时更新状态变量的值,式(13)告诉我们,观测数据是如何影响状态变量的。如果不想实时更新,就可以仅用式(10)。
根据式(10),Ft和Ht的具体形式为
(14)
(15)
(16)
在t时刻,根据式(4)预测F的当前位置,根据式(5)得到终端C得到的GPS数据的预测值。使用t-1时刻的最优状态估计,代入式(4)得
(17)
的covariance更新如下,其中covariance用P表示
(18)
是的covariance,是的covariance。式(17)、(18)完成了预测,如何结合新的观测求解最优估计呢,继续往后看。t时刻的观测变量的预测
(19)
观测变量的covariance
(20)
Kalman增益
(21)
t时刻观测变量的真实值与预测值之间的残差
(22)
t时刻观测变量的最优估计
(23)
其covariance的最优估计是
(24)
公式(17)-(24)可以使用图3解释(图3使用观测变量来表示,而没有具体描述状态变量的预测和寻优的过程)。公式(17)-(19)对应的是图3b,根据图3a的t-1时刻的最优估计预测t时刻的观测变量。公式(20)-(24)对应的是图3d,根据图3c的新观测变量计算最优状态变量和观测变量。
(25)
(26)
首先根据状态转移模型计算状态值的预测,求得观测变量的预测值。然后获得新的观测变量。再结合观测变量和观测变量的预测值,求出状态和观测变量的最优估计值。下面给出的是t时刻最优估计的模型,依然是高斯的。
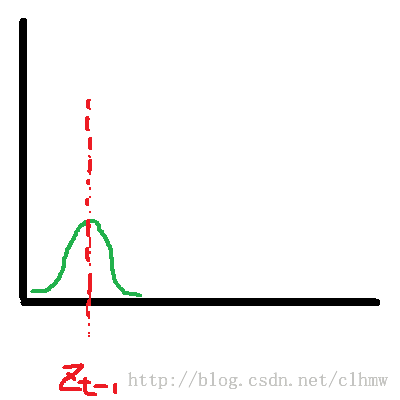
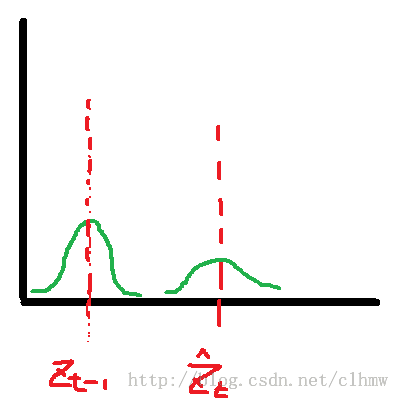
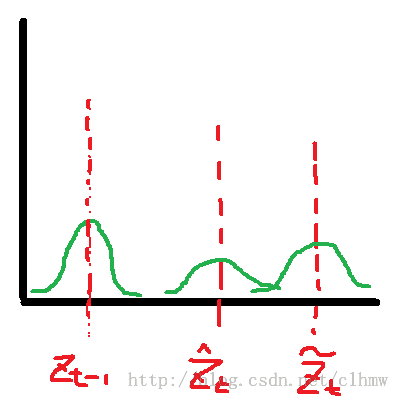
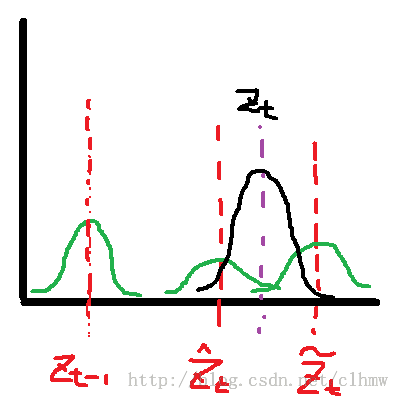
a b c d
图3 F位置估计
Kalman Filter的matlab代码
% the data to estimate
lens=100;
a=2;
b=50;
x=1:lens;
y=a*x+b*randn(1,lens);
D=[x;y];
% the number of the stateparamters
StateParamNum=4;
% the number of thecontrol parameters
ContrParamNum=2;
% the number of theobservation parameters
ObsevParamNum=2;
% the motion transitionmatrix
F=[1 0 1 0;0 1 0 1;0 0 1 0;0 00 1];
% the control matrix
G=[0.5 0;0 0.5;1 0;0 1];
% the observation matrix
H=[1 0 0 0;0 1 0 0];
% the state vector
X=zeros(StateParamNum,1);
X=[D(1,1);D(2,1);0.001;0.001];
% the control vector
U=0*randn(2,1);
% the observation vector
Z=zeros(ObsevParamNum,1);
% the covariance of thestate
P=eye(StateParamNum,StateParamNum);
P(1,1)=10;
P(2,2)=10;
P(3,3)=10;
P(4,4)=10;
% the covariance of thestate noise
q=eye(StateParamNum,StateParamNum);
q(1,1)=0.1;
q(2,2)=0.1;
q(3,3)=0.01;
q(4,4)=0.01;
% the covariance of theobserve noise
r=eye(ObsevParamNum,ObsevParamNum);
r(1,1)=10;
r(2,2)=10;
% the optimal estimationof the the state
Xf=zeros(StateParamNum,lens);
% the optimal estimationof the the observation
Zf=zeros(ObsevParamNum,lens);
V=zeros(ObsevParamNum,lens);
Pf=zeros(StateParamNum,lens);
for i=1:lens
% theestimation of the state in time t
Xest=F*X+G*U;
% thecovariance of the estimated state
Pest=F*P*F'+q;
% theestimation of the observation in time t
Zest=H*Xest;
% thecovariance of the estimated observation
Sest=H*Pest*H'+r;
% theKalman Gain
K=Pest*H'*inv(Sest);
% thedifference between estimation and observation
v=D(:,i)-Zest;
% theoptimal estimation of the state in time t
X=Xest+K*v;
% thecovariance of the optimal state
P=(eye(StateParamNum,StateParamNum)-K*H)*Pest;
% theoptimal estimation of the observation in time t
Z=H*X;
Xf(:,i)=X;
Zf(:,i)=Z;
V(:,i)=v;
Pf(:,i)=diag(P);
end
figure(1)
hold on
colormax=lens+1;
c=(1:lens-1)/colormax;
c1=repmat(c,3,1);
c2=[ones(1,lens-1);repmat(c,2,1)];
for i=1:lens-1
plot(D(1,i:i+1),D(2,i:i+1),...
'LineWidth',3,'Color',c1(:,i)');
plot(Zf(1,i:i+1),Zf(2,i:i+1),'-+',...
'LineWidth',1,'Color',[1 0 0]);
end
hold off
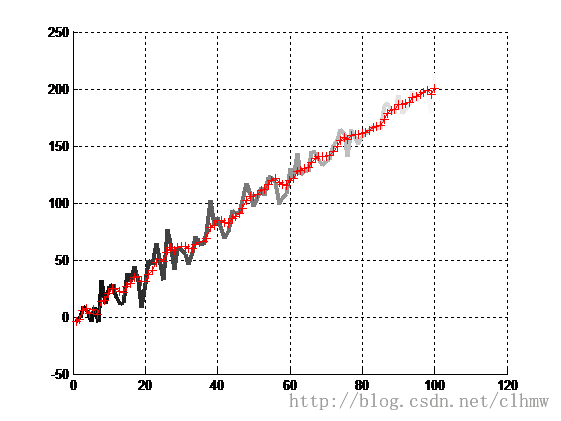
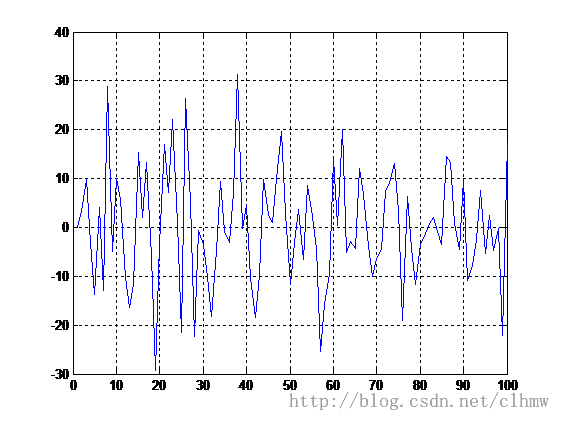
a b
图4 a、原始数据和滤波数据;b、拟合误差
上面这段代码中去掉了控制部分,调整q和r可以改善滤波的效果。
在上面的推导过程中,对Kalman滤波有以下几点认识
1、 模型是线性的,体现在公式(4)中;
2、 模型是高斯的,体现在公式(4)、(5)中;
3、式(4)中的F和G矩阵没有更新;
4、状态变量是根据设计者的知识给出的。
综合以上几点,Kalman滤波是一个预设的跟踪器,物体的运动模型,运动之间的关系都是给定的。
我们可以默认这些预设都是正确的,直接来用。但是,人作为第一发现者,是如何从数据中抽象出这些状态,如何从状态到状态的转移求得运动模型,这些都没有解决。如果,这个问题没有解决,我们将无法进入下一个螺旋上升的阶段。说到这里,我不得不怀疑这样一点——我们获得的所谓的运动模型,所谓的状态变量的内容,是不是某些非人类的文明灌输给我们的。如果是这样的,那么我们不可能发现螺旋上升的途径;如果不是这样,这些是我们自己发现的,那么我们就有办法重新发现“发现知识”的过程,指导我们进入下一个螺旋。