基于Tire树和最大概率法的中文分词功能的Java实现
对于分词系统的实现来说,主要应集中在两方面的考虑上:一是对语料库的组织,二是分词策略的制订。
1. Tire树
Tire树,即字典树,是通过字串的公共前缀来对字串进行统计、排序及存储的一种树形结构。其具有如下三个性质:
1) 根节点不包含字符(或汉字),除根节点以外的每个节点只能包含一个字符(汉字)
2) 从根节点到任一节点的路径上的所有节点中的字符(汉字)按顺序排列的字符串(词组)就是该节点所对应的字符串(词组)
3) 每个节点的所有直接子节点包含的字符(汉字)各不相同
上述性质保证了从Tire树中查找任意字符串(词组)所需要比较的次数尽可能最少,以达到快速搜索语料库的目的。
如下图所示的是一个由词组集<一,一万,一万多,一万元,一上午,一下午,一下子>生成的Tire树的子树:
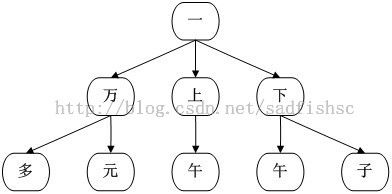
可见,从子树的根节点“一”开始,任意一条路径都能组成一个以“一”开头的词组。而在实际应用中,需要给每个节点附上一些数据属性,如词频,因而可以用这些属性来区别某条路径上的字串是否是一个词组。如,节点“上”的词频为-1,那么“一上”就不是一个词组。
如下的代码是Tire树的Java实现:
package chn.seg;
import java.util.HashMap;
import java.util.Map;
public class TireNode {
private String character;
private int frequency = -1;
private double antilog = -1;
private Map<String, TireNode> children;
public String getCharacter() {
return character;
}
public void setCharacter(String character) {
this.character = character;
}
public int getFrequency() {
return frequency;
}
public void setFrequency(int frequency) {
this.frequency = frequency;
}
public double getAntilog() {
return antilog;
}
public void setAntilog(double antilog) {
this.antilog = antilog;
}
public void addChild(TireNode node) {
if (children == null) {
children = new HashMap<String, TireNode>();
}
if (!children.containsKey(node.getCharacter())) {
children.put(node.getCharacter(), node);
}
}
public TireNode getChild(String ch) {
if (children == null || !children.containsKey(ch)) {
return null;
}
return children.get(ch);
}
public void removeChild(String ch) {
if (children == null || !children.containsKey(ch)) {
return;
}
children.remove(ch);
}
}
2. 最大概率法(动态规划)
最大概率法是中文分词策略中的一种方法。相较于最大匹配法等策略而言,最大概率法更加准确,同时其实现也更为复杂。
基于动态规划的最大概率法的核心思想是:对于任意一个语句,首先按语句中词组的出现顺序列出所有在语料库中出现过的词组;将上述词组集中的每一个词作为一个顶点,加上开始与结束顶点,按构成语句的顺序组织成有向图;再为有向图中每两个直接相连的顶点间的路径赋上权值,如A→B,则AB间的路径权值为B的费用(若B为结束顶点,则权值为0);此时原问题就转化成了单源最短路径问题,通过动态规划解出最优解即可。
如句子“今天下雨”,按顺序在语料库中存在的词组及其费用如下:
今,a
今天,b
天,c
天下,d
下,e
下雨,f
雨,g
则可以生成如下的加权有向图:

显而易见,从“Start”到“End”的单源路径最优解就是“今天下雨”这个句子的分词结果。
那么,作为权值的费用如何计算呢?对于最大概率法来说,要求的是词组集在语料库中出现的概率之乘积最大。对应单源最短路径问题的费用来说,
费用 = log( 总词频 / 某一词组词频 )
通过上述公式就可以把“最大”问题化为“最小”问题,“乘积”问题化为“求和”问题进行求解了。
如下的代码是基于动态规划的最大概率法的Java实现:
package chn.seg;
import java.io.BufferedReader;
import java.io.File;
import java.io.FileInputStream;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.List;
public class ChnSeq {
private TireNode tire = null;
public void init() throws IOException, ClassNotFoundException {
File file = new File("data" + File.separator + "dict.txt");
if (!file.isFile()) {
System.err.println("语料库不存在!终止程序!");
System.exit(0);
}
BufferedReader in = new BufferedReader(
new InputStreamReader(new FileInputStream(file), "utf-8"));
String line = in.readLine();
int totalFreq = Integer.parseInt(line);
tire = new TireNode();
while ((line = in.readLine()) != null) {
String[] segs = line.split(" ");
String word = segs[0];
int freq = Integer.parseInt(segs[1]);
TireNode root = tire;
for (int i = 0; i < word.length(); i++) {
String c = "" + word.charAt(i);
TireNode node = root.getChild(c);
if (node == null) {
node = new TireNode();
node.setCharacter(c);
root.addChild(node);
}
root = node;
}
root.setFrequency(freq);
root.setAntilog(Math.log((double)totalFreq / freq));
}
in.close();
}
public TireNode getTire() {
return tire;
}
public TireNode getNodeByWord(String word) {
if (tire == null) {
System.err.println("需要先初始化ChnSeq对象!");
return null;
}
TireNode node = tire;
for (int i = 0; i < word.length(); i++) {
String ch = word.charAt(i) + "";
if (node == null) {
break;
} else {
node = node.getChild(ch);
}
}
return node;
}
private class Segment {
public String word;
public String endChar;
public String lastChar;
public double cost;
public final static String START_SIGN = "<< STARTING >>";
public final static String END_SIGN = "<< ENDING >>";
}
private List<Segment> preSegment(String sentence) {
List<Segment> segs = new ArrayList<Segment>();
Segment terminal = new Segment();
terminal.word = Segment.START_SIGN;
terminal.endChar = Segment.START_SIGN;
terminal.lastChar = null;
segs.add(terminal);
for (int i = 0; i < sentence.length(); i++) {
for (int j = i + 1; j <= sentence.length(); j++) {
String word = sentence.substring(i, j);
TireNode tnode = this.getNodeByWord(word);
if (tnode == null) {
break;
}
if (tnode.getFrequency() <= 0) {
continue;
}
Segment seg = new Segment();
seg.word = word;
seg.endChar = word.substring(word.length() - 1, word.length());
if (i == 0) {
seg.lastChar = Segment.START_SIGN;
} else {
seg.lastChar = sentence.substring(i - 1, i);
}
seg.cost = tnode.getAntilog();
segs.add(seg);
}
}
terminal = new Segment();
terminal.word = Segment.END_SIGN;
terminal.endChar = Segment.END_SIGN;
terminal.lastChar = sentence.substring(sentence.length() - 1, sentence.length());
segs.add(terminal);
return segs;
}
private String[] dynamicSegment(List<Segment> segs) {
final double INFINITE = 9999999;
if (segs == null || segs.size() == 0) {
return null;
}
int n = segs.size();
double[][] costs = new double[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
costs[i][j] = INFINITE;
}
}
for (int i = 0; i < n; i++) {
String endChar = segs.get(i).endChar;
for (int j = 0; j < n; j++) {
String lastChar = segs.get(j).lastChar;
if (lastChar != null && lastChar.equals(endChar)) {
costs[i][j] = segs.get(j).cost;
}
}
}
int sp = 0; // starting point
int fp = n - 1; // finishing point
double[] dist = new double[n];
List<List<Integer>> sPaths = new ArrayList<List<Integer>>();
List<Integer> list = new ArrayList<Integer>();
for (int i = 0; i < n; i++) {
dist[i] = costs[sp][i];
if (sp != i) {
list.add(i);
}
if (dist[i] < INFINITE) {
List<Integer> spa = new ArrayList<Integer>();
sPaths.add(spa);
} else {
sPaths.add(null);
}
}
while (!list.isEmpty()) {
Integer minIdx = list.get(0);
for (int i: list) {
if (dist[i] < dist[minIdx]) {
minIdx = i;
}
}
list.remove(minIdx);
for (int i = 0; i < n; i++) {
if (dist[i] > dist[minIdx] + costs[minIdx][i]) {
dist[i] = dist[minIdx] + costs[minIdx][i];
List<Integer> tmp = new ArrayList<Integer>(sPaths.get(minIdx));
tmp.add(minIdx);
sPaths.set(i, tmp);
}
}
}
String[] result = new String[sPaths.get(fp).size()];
for (int i = 0; i < sPaths.get(fp).size(); i++) {
result[i] = segs.get(sPaths.get(fp).get(i)).word;
}
return result;
}
public String[] segment(String sentence) {
return dynamicSegment(preSegment(sentence));
}
}
3. 测试代码
package chn.seg;
import java.io.IOException;
public class Main {
public static void main(String[] args) throws ClassNotFoundException, IOException {
ChnSeq cs = new ChnSeq();
cs.init();
String sentence = "生活的决定权也一直都在自己手上";
String[] segs = cs.segment(sentence);
for (String s: segs) {
System.out.print(s + "\t");
}
}
}