标准粒子群算法(PSO)
第2章 标准粒子群算法(PSO)
2.1 粒子群算法思想的起源
粒子群优化(Particle Swarm Optimization, PSO)算法是Kennedy和Eberhart受人工生命研究结果的启发、通过模拟鸟群觅食过程中的迁徙和群聚行为而提出的一种基于群体智能的全局随机搜索算法,自然界中各种生物体均具有一定的群体行为,而人工生命的主要研究领域之一是探索自然界生物的群体行为,从而在计算机上构建其群体模型。自然界中的鸟群和鱼群的群体行为一直是科学家的研究兴趣,生物学家Craig Reynolds在1987年提出了一个非常有影响的鸟群聚集模型,在他的仿真中,每一个个体遵循:
(1) 避免与邻域个体相冲撞;
(2) 匹配邻域个体的速度;
(3) 飞向鸟群中心,且整个群体飞向目标。
仿真中仅利用上面三条简单的规则,就可以非常接近的模拟出鸟群飞行的现象。1995年,美国社会心理学家James Kennedy和电气工程师Russell Eberhart共同提出了粒子群算法,其基本思想是受对鸟类群体行为进行建模与仿真的研究结果的启发。他们的模型和仿真算法主要对Frank Heppner的模型进行了修正,以使粒子飞向解空间并在最好解处降落。Kennedy在他的书中描述了粒子群算法思想的起源。
2.2 算法原理
PSO从这种模型中得到启示并用于解决优化问题。PSO 中,每个优化问题的潜在解都是搜索空间中的一只鸟,称之为粒子。所有的粒子都有一个由被优化的函数决定的适值( fitness value) ,每个粒子还有一个速度决定它们飞翔的方向和距离。然后粒子们就追随当前的最优粒子在解空间中搜索。
PSO初始化为一群随机粒子(随机解),然后通过迭代找到最优解。在每一次迭代中,粒子通过跟踪两个极值来更新自己;第一个就是粒子本身所找到的最优解,这个解称为个体极值;另一个极值是整个种群目前找到的最优解,这个极值是全局极值。另外也可以不用整个种群而只是用其中一部分作为粒子的邻居,那么在所有邻居中的极值就是局部极值。
假设在一个![]() 维的目标搜索空间中,有
维的目标搜索空间中,有![]() 个粒子组成一个群落,其中第
个粒子组成一个群落,其中第![]() 个粒子表示为一个
个粒子表示为一个![]() 维的向量
维的向量
整个粒子群迄今为止搜索到的最优位置为全局极值,记为
在找到这两个最优值时,粒子根据如下的公式(2-1)和( 2-2)来更新自己的速度和位置:
其中:![]() 和
和![]() 为学习因子,也称加速常数(acceleration constant),w为惯性因子,
为学习因子,也称加速常数(acceleration constant),w为惯性因子,![]() 和
和![]() 为[0,1]范围内的均匀随机数。式(2-1)右边由三部分组成,第一部分为“惯性(inertia)”或“动量(momentum)”部分,反映了粒子的运动“习惯(habit)”,代表粒子有维持自己先前速度的趋势;第二部分为“认知(cognition)”部分,反映了粒子对自身历史经验的记忆(memory)或回忆(remembrance),代表粒子有向自身历史最佳位置逼近的趋势;第三部分为“社会(social)”部分,反映了粒子间协同合作与知识共享的群体历史经验,代表粒子有向群体或邻域历史最佳位置逼近的趋势,
为[0,1]范围内的均匀随机数。式(2-1)右边由三部分组成,第一部分为“惯性(inertia)”或“动量(momentum)”部分,反映了粒子的运动“习惯(habit)”,代表粒子有维持自己先前速度的趋势;第二部分为“认知(cognition)”部分,反映了粒子对自身历史经验的记忆(memory)或回忆(remembrance),代表粒子有向自身历史最佳位置逼近的趋势;第三部分为“社会(social)”部分,反映了粒子间协同合作与知识共享的群体历史经验,代表粒子有向群体或邻域历史最佳位置逼近的趋势, ![]() ,
,![]() 是粒子的速度,
是粒子的速度,![]() ,
,![]() 是常数,由用户设定用来限制粒子的速度。
是常数,由用户设定用来限制粒子的速度。![]() 和
和![]() 是介于
是介于![]() 之间的随机数。
之间的随机数。
2.3 标准粒子群算法流程
算法的流程如下:
Step1:初始化粒子群,包括群体规模![]() ,每个粒子的位置
,每个粒子的位置![]() 和速度
和速度![]()
Step3: 对每个粒子,用它的适应度值![]() 和个体极值
和个体极值![]() 比较,如果
比较,如果![]() ,则用
,则用![]() 替换掉
替换掉![]() ;
;
Step4: 对每个粒子,用它的适应度值![]() 和全局极值
和全局极值![]() 比较,如果
比较,如果![]() 则用
则用![]() 替
替![]() ;
;
Step5: 根据公式(2-1),(2-2)更新粒子的速度![]() 和位置
和位置![]() ;
;
Step6: 如果满足结束条件(误差足够好或到达最大循环次数)退出,否则返回Step2。
图2-1. PSO算法流程图
2.4 特点
1、式(2-1)中第1部分可理解为粒子先前的速度或惯性;第2部份可理解为粒子的“认知”行为,表示粒子本身的思考能力;第3部分可理解为粒子的“社会”行为,表示粒子之间的信息共享与相互合作。公式(2-2) 表示了粒子在求解空间中,由于相互影响导致的运动位置调整。整个求解过程中,加速因子![]() 和
和![]() 和最大速度
和最大速度![]() 共同维护粒子对全局和局部搜索能力的平衡。
共同维护粒子对全局和局部搜索能力的平衡。
2、粒子群优化算法初期,其解群随进化代数表现了更强的随机性,正是由于其产生了下一代解群的较大的随机性,以及每代所有解的“信息”的共享性和各个解的“自我素质”的提高。
3、PSO 的一个优势就是采用实数编码,不需要像遗传算法一样采用二进制编码(或者采用针对实数的遗传操作) 。例如对于问题![]() 求解, 粒子可以直接编码为
求解, 粒子可以直接编码为![]() ,而适应度函数就是
,而适应度函数就是![]() 。
。
4、粒子具有“记![]() 忆”的特性,它们通过“自我”学习和向“他人”学习,使其下一代解有针对性的从“先辈”那里继承更多的信息,从而能在较短的时间内找到最优解。
忆”的特性,它们通过“自我”学习和向“他人”学习,使其下一代解有针对性的从“先辈”那里继承更多的信息,从而能在较短的时间内找到最优解。
5、与遗传算法相比,粒子群优化算法的信息共享机制是很不同的:在遗传算法中,染色体互相共享信息,所以整个种群的移动是比较均匀的向最优区域移动;在粒子群优化算法中,信息流动是单向的,即只有![]() 将信息给其他的粒子,这使得整个搜索更新过程跟随当前解。
将信息给其他的粒子,这使得整个搜索更新过程跟随当前解。
2.5 惯性权重线性递减的粒子群算法(PSO-W)
探索是偏离原来的寻优轨迹去寻找一个更好的解,探索能力是一个算法的全局搜索能力。开发是利用一个好的解,继续原来的寻优轨迹去搜索更好的解,它是算法的局部搜索能力。如何确定局部搜索能力和全局搜索能力的比例,对一个问题的求解过程很重要。1998年,Yuhui Shi[9]提出了带有惯性权重的改进粒子群算法。其进化过程为:
在式(2-1)中,第一部分表示粒子先前的速度,用于保证算法的全局收敛性能;第二部分、第三部分则是使算法具有局部收敛能力。可以看出,式(2-3)中惯性权重![]() 表示在多大程度上保留原来的速度。
表示在多大程度上保留原来的速度。![]() 较大,全局收敛能力强,局部收敛能力弱;
较大,全局收敛能力强,局部收敛能力弱;![]() 较小,局部收敛能力强,全局收敛能力弱。
较小,局部收敛能力强,全局收敛能力弱。
当![]() 时,式(2-3)与式(2-1)完全一样,表明带惯性权重的粒子群算法是基本粒子群算法的扩展。实验结果表明,
时,式(2-3)与式(2-1)完全一样,表明带惯性权重的粒子群算法是基本粒子群算法的扩展。实验结果表明,![]() 在
在![]() 之间时,PSO算法有更快的收敛速度,而当
之间时,PSO算法有更快的收敛速度,而当![]() 时,算法则易陷入局部极值。
时,算法则易陷入局部极值。
由于较大的权重因子有利于跳出局部最小点,便于全局搜索,而较小的惯性因子则有利于对当前的搜索区域进行精确局部搜索,以利于算法收敛,因此针对PSO算法容易早熟以及算法后期易在全局最优解附近产生振荡现象,可以采用线性变化的权重,让惯性权重从最大值![]() 线性减小到最小值
线性减小到最小值![]() 。随算法迭代次数的变化公式为:
。随算法迭代次数的变化公式为:
其中,![]() ,
,![]() 分别表示
分别表示![]() 的最大值和最小值,t表示当前迭代步数,
的最大值和最小值,t表示当前迭代步数,![]() 表示最大迭代步数,通常取
表示最大迭代步数,通常取![]() ,
,![]() .
.
2.6 带收缩因子的粒子群算法(PSO-X)
学习因子cl和c2决定了微粒本身经验信息和其他微粒的经验信息对微粒运行轨迹的影响,反映了微粒群之间的信息交流。设置c1较大的值,会使微粒过多地在局部范围内徘徊,而较大的c2的值,则又会促使微粒过早收敛到局部最小值。微粒有效地控制微粒的飞行速度,使算法达到全局探测与局部开采两者间的有效平衡,Clerc构造了引入收缩因子的PSO模型,采用了压缩因子,这种调整方法通过合适选取参数,可确保PSO算法的收敛性,并可取消对速度的边界限制。速度公式如下:
2.7测试仿真函数
用2个单峰函数和2个多峰函数来测试以上三种算法,求函数的最小值,
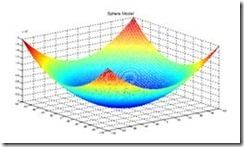
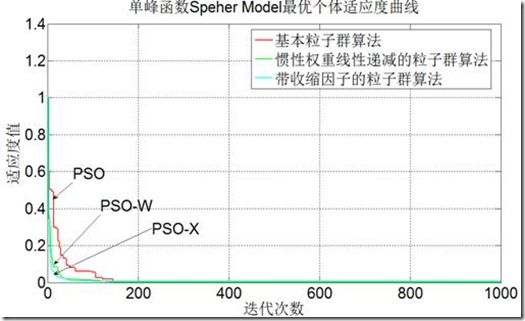
1.单峰函数-Sphere Model
函数维数为2时的模型为:
Sphere Model Schwefel’s Problem2.22
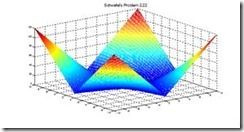
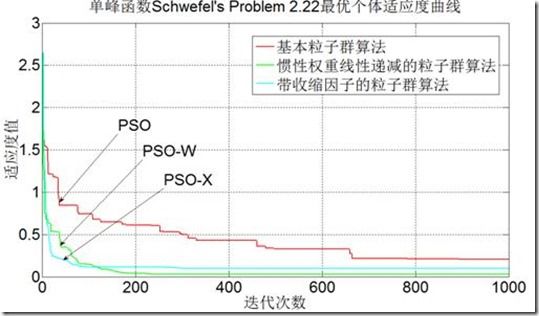
2.单峰函数 Schwefel’s Problem2.22
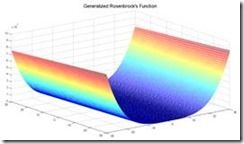
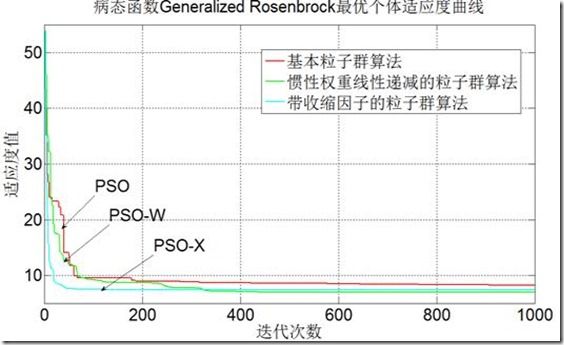
3.病态函数Generalized Rosenbrock
Generalized Rosenbrock Generalized Rastrigin
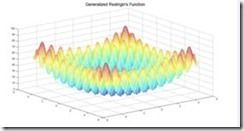
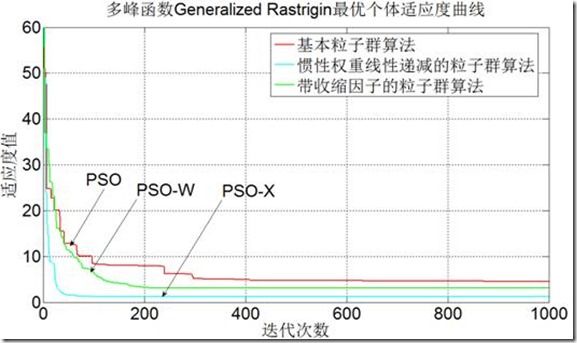
4.多峰函数Generalized Rastrigin 函数
2.8测试结果
初始条件为粒子群数目为20,每个粒子维数为20,迭代1000次
图2-2单峰函数Sphere Model 测试结果
图2-3单峰函数Schwefel’s Problem2.22 测试结果
图2-4病态函数Generalized Rosenbrock 测试结果
图2-5多峰函数Generalized Rastrigin测试结果
表2-1 基本粒子群算法、惯性权重线减粒子群算法,带收缩因子粒子群算法输出结果
| 函数 |
PSO |
PS0-W |
PSO-X |
||
| 单峰 函数 |
最优值 |
0.0021(好解) |
2.56E-05(好解) |
2.45E-04(好解) |
|
| 均值 |
0.0233 |
0.0084 |
0.0041 |
||
| 最优值 |
0.1129(差解) |
0.0754(好解) |
0.0849(好解) |
||
| 均值 |
0.3304 |
0.1275 |
0.1011 |
||
| 病态函数 |
最优值 |
8.5907(差解) |
7.7378(差解) |
8.2623(差解) |
|
| 均值 |
9.9060 |
8.4721 |
8.5427 |
||
| 多峰函数 |
最优值 |
1.2151(差解) |
1.2344(差解) |
0.8977(差解) |
|
| 均值 |
3.4962 |
1.678 |
1.209 |
2.9测试结论
从上图2-2~2-5及表一我们可以知道,以上三种粒子群算法,只对于单峰函数且非病态方程才能取得最优解,迭代次数越多,种群数目越多,得到的精度就会越高,但同时也会延长运算的时间,所以迭代次数和种群数需设置好,并且相对来说惯性权重线性递减的粒子群算法找到的解是最好的。
然而对于多峰函数以及病态方程,以上三种粒子群算法无法取得最好的解,无论是增加迭代次数还是种群数目,精度都不会有太大的改变,这就是基本粒子群一个最大的缺点,即容易陷入局部最优解的位置,算法容易早熟,对多峰函数或病态函数无法找到最优解,所以我们可以得出惯性权重线减粒子群算法,带收缩因子粒子群算法改进的效果意义不大,算法没有本质上的改变,精度也无法提高很多。
由于在我们实际生活中,大部份的优化问题都是多峰函数或病态函数,为了克服基本粒子群算法的缺陷,我研究了以下四种改进的粒子群算法:基于混沌思想改进的粒子群算法、基于遗传思想改进的混合粒子群算法、基于免疫记忆和浓度机制改进的混合粒子群算法.