BP神经网络
由于课题需要学习神经网络也有一段时间了，每次只是调用一下matlab的newff函数设置几个参数，就自以为掌握了。真是可笑，会了其实只是会使用，一知半解而已。
本来想写人工神经网络，但是范围太广，无法驾驭，姑且就先写BP吧，因为BP是目前应用最广泛的神经网络模型之一。
一.人工神经网络
人工神经网络（ANN）的研究在一定程度上收到了生物学的启发，因为生物的学习系统是有相互连接的神经元（neuron）组成的异常复杂的网络。而人工神经网络与此大体相似，它是由一系列简单神经元相互密集连接构成，其中每一个神经元有一定数量的实值输入（也可以是其他神经元的输出），并产生单一的实数输出（可能成为其他很多神经元的输入）。
下图是一个人工神经元模型，可以帮助理解：
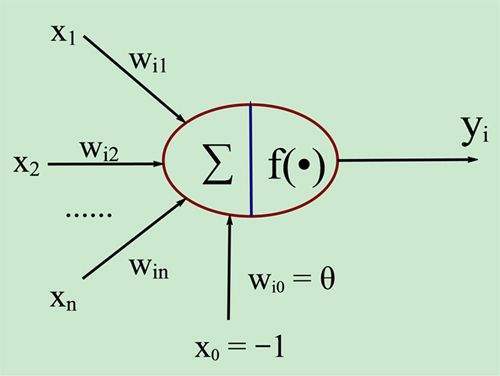
其中：X1~Xn是从其他神经元传来的输入信号，Wij表示从神经元j到神经元i的连接权值，θ表示阈值（threshold），f为激活函数，Yi为神经元i输出。
二.适合神经网络学习的问题
ANN适合具有以下特征的问题：
1.实例是用很多“属性-值”对表示的；
2.目标函数的输出可能是离散值、实数值或者由若干实数属性或离散属性组成的向量；
3.训练数据可能包含错误；
4.可容忍长时间的训练；
5.可能需要快速求出目标函数值；
6.人类能否理解学到的目标函数是不重要的。
与其说这些是适合ANN的问题，不如说ANN本身特征如此，适用于这些问题。
三.BP算法
BP算法是一种按误差逆传播算法训练的多层前馈网络。前馈网络只在训练过程中会有反馈信号，而在分类过程中数据只能向前传送，直到到达输出层，层间没有向后的反馈信号。也就是说，训练时权值W会根据反馈信号不断更新，得到一个学习机net，而分类的时候直接使用net中训练好的W，不需要再更新。
1.基本原理
利用输出后的误差来估计输出层的直接前导层的误差，再用这个误差估计前一层的误差，如此一层一层的反传下去，就获得了所有其他各层的误差估计。
2.三层BP网络模型
根据Kolrnogorov定理，一个3层BP神经网络能够实现对任意非线性函数进行逼近，一个典型的3层BP神经网络模型如下：
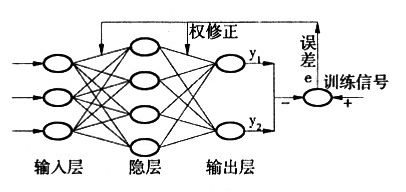3.激活函数
激活函数必须处处可导，一般都使用S型函数。
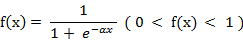
4.算法推导
好吧，到了最为繁琐也最为重要的一部分，这也能够区分“会使用”和“真正掌握”。
首先给出一些定义：
输入层有n个神经元，隐含层有p个神经元，输出层有q个神经元；
输入向量：x=(x1,x2,...,xn)
隐含层输入向量：hi=(hi1,hi2,...,hip)
隐含层输出向量：ho=(ho1,ho2,...,hop)
输出层输入向量：yi=(yi1,yi2,...yiq)
输出层输出向量：yo=(yo1,yo2,...yoq)
期望输出向量：d=(d1,d2,...,dq)
输入层与隐含层的连接权值：Wih
隐含层与输出层的连接权值：Who
隐含层各神经元的阈值：bh
输出层各神经元的阈值：bo
样本数据个数：k=1,2,...,m
激活函数：S型函数
误差函数：
算法步骤：
对给予的一个输入样本，计算隐含层各神经元的输入输出：
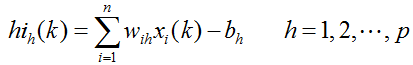
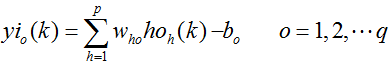
利用网络期望输出和实际输出，计算误差函数对输出层各神经元的偏导数δo(k):
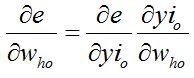
利用隐含层到输出层的连接权值、输出层的δo(k)和隐含层的输出计算误差函数对隐含层各神经元的偏导数δh(k):
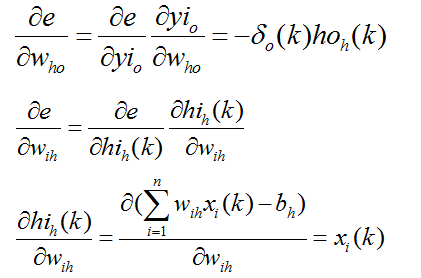
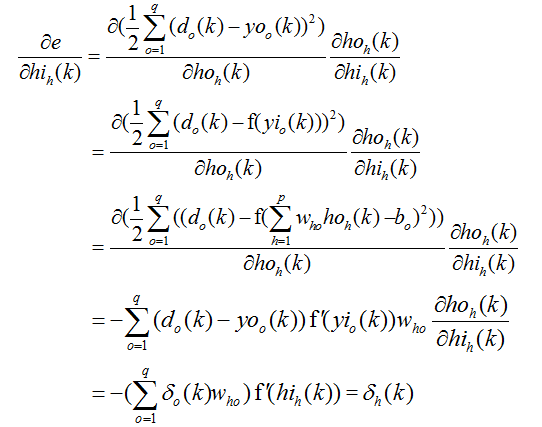
利用输出层各神经元的δo(k)和隐含层各神经元的输出来修正连接权值Who(k)：
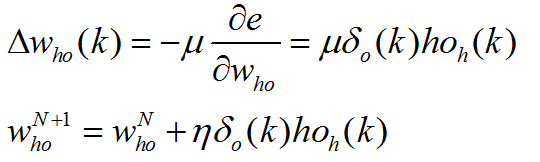
隐含层各神经元的δh(k)和输入层各神经元的输入修正连接权Wih(k)：
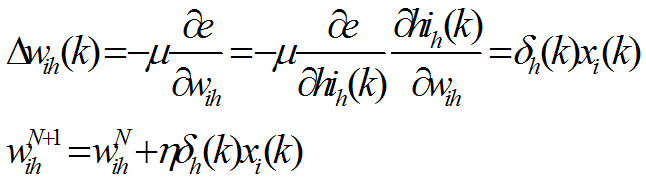
计算全局误差，判断网络误差是否满足要求。当误差达到预设精度或学习次数大于设定的最大次数，则结束算法。否则，选取下一个学习样本及对应的期望输出，进入下一轮学习。
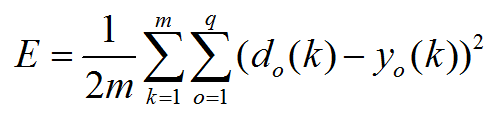
当误差达到预设精度或学习次数大于设定的最大次数，则结束算法。否则，选取下一个学习样本及对应的期望输出，进入下一轮学习。
5.编程实验
好了，看懂了BP的算法步骤，再给出一个BP算法C语言实例帮助理解：
#include"stdafx.h"
#include<iostream>
#include<cmath>
#include<vector>
#include<algorithm>
#include<ctime>
using namespace std;
//输入一对数(x,y),输出为xxxx(x=0或1)
//判断(x,y)在第几象限，若在第一象限，则输出1000，以此类推;
//样本为随机的1000对(x,y)
//对指定输入对求其所在象限；
const int inputnode=2;//输入层神经元个数
const int hidenode=4;//隐含层神经元个数
const int outputnode=4;//输出层神经元个数
const int sample_num=1000;//样本个数
double w_ih[inputnode][hidenode];//输入层隐含层间权值矩阵
double w_ho[hidenode][outputnode];//隐含层输出层间权值矩阵
double sita_h[hidenode];//隐含层间阈值
double sita_o[outputnode];//输出层间阈值
double sample[sample_num][inputnode];
double sample_label[sample_num][outputnode];
double error[sample_num];
double totalerror=0;
double x[sample_num][inputnode];//网络输入
double a[sample_num][hidenode];//隐层的输出
double y[sample_num][outputnode];//网络输出
double d[sample_num][outputnode];//样本参考输出
double delta_ih[sample_num][hidenode];//输入到隐层的权值修正
double delta_ho[sample_num][outputnode];//隐层到输出的权值修正
const int epochs=10000;//迭代次数
const double goal=0.15;//误差目标精度
const double lr=0.01;//学习速率
int count=0;
void init()
{
//生成样本
int i,j;
srand((unsigned)time(NULL));
for(i=0;i<sample_num;i++)
{
sample[i][0]=(double)(rand()%20000-10000)/10000;
sample[i][1]=(double)(rand()%20000-10000)/10000;
if(sample[i][0]>0&&sample[i][1]>0)
{
sample_label[i][0]=1;
sample_label[i][1]=0;
sample_label[i][2]=0;
sample_label[i][3]=0;
}
if(sample[i][0]<0&&sample[i][1]>0)
{
sample_label[i][0]=0;
sample_label[i][1]=1;
sample_label[i][2]=0;
sample_label[i][3]=0;
}
if(sample[i][0]<0&&sample[i][1]<0)
{
sample_label[i][0]=0;
sample_label[i][1]=0;
sample_label[i][2]=1;
sample_label[i][3]=0;
}
if(sample[i][0]>0&&sample[i][1]<0)
{
sample_label[i][0]=0;
sample_label[i][1]=0;
sample_label[i][2]=0;
sample_label[i][3]=1;
}
}
//初始化权值矩阵
for(i=0;i<inputnode;i++)
{
for(j=0;j<hidenode;j++)
{
w_ih[i][j]=(double)(rand()%20000-10000)/100000;
}
}
for(i=0;i<hidenode;i++)
{
for(j=0;j<outputnode;j++)
{
w_ho[i][j]=(double)(rand()%20000-10000)/100000;
}
}
//初始化阈值
for(i=0;i<hidenode;i++)
{
sita_h[i]=(double)(rand()%1000)/1000;
}
for(i=0;i<outputnode;i++)
{
sita_o[i]=(double)(rand()%1000)/1000;
}
//初始化误差
for(i=0;i<sample_num;i++)
{
error[i]=0;
}
//初始化权值调整系数
for(i=0;i<sample_num;i++)
{
for(j=0;j<hidenode;j++)
{
delta_ih[i][j]=0;
}
}
for(i=0;i<sample_num;i++)
{
for(j=0;j<outputnode;j++)
{
delta_ho[i][j]=0;
}
}
}
void train()
{
cout<<"BP网络开始训练:"<<endl;
int i,j,k;
for(int loop=0;loop<epochs;loop++)
{
totalerror=0;
int count=0;
for(i=0;i<sample_num;i++)
{
//读入样本
x[count][0]=sample[count][0];
x[count][1]=sample[count][1];
d[count][0]=sample_label[count][0];
d[count][1]=sample_label[count][1];
d[count][2]=sample_label[count][2];
d[count][3]=sample_label[count][3];
//计算隐含层输出
double net_h[hidenode];
for(j=0;j<hidenode;j++)
{
net_h[j]=w_ih[0][j]*x[count][0]+w_ih[1][j]*x[count][1]-sita_h[j];
a[count][j]=1/(1+exp(-net_h[j]));
}
//计算输出层输出
double net_o[outputnode];
for(k=0;k<outputnode;k++)
{
net_o[k]=0;
for(j=0;j<hidenode;j++)
{
net_o[k]+=w_ho[j][k]*a[count][j];
}
net_o[k]-=sita_o[k];
y[count][k]=1/(1+exp(-net_o[k]));
}
//计算样本误差
for(k=0;k<outputnode;k++)
{
error[count]+=(d[count][k]-y[count][k])*(d[count][k]-y[count][k]);
}
error[count]/=2;
//计算隐含层输出层间权值调整系数
for(k=0;k<outputnode;k++)
{
delta_ho[count][k]=(d[count][k]-y[count][k])*y[count][k]*(1-y[count][k]);
}
//计算输入层到隐含层的权值调整系数
for(j=0;j<hidenode;j++)
{
for(k=0;k<outputnode;k++)
{
delta_ih[count][j]+=delta_ho[count][k]*w_ho[j][k]*a[count][j]*(1-a[count][j]);
}
}
totalerror+=error[count];
count++;
}
cout<<"第"<<loop+1<<"次迭代,"<<"总体方差为："<<totalerror<<endl;
//调整w_ih
double temp=0.0;
for(i=0;i<inputnode;i++)
{
for(j=0;j<hidenode;j++)
{
temp=0;
for(k=0;k<sample_num;k++)
{
temp+=delta_ih[k][j]*x[k][i];
}
w_ih[i][j]+=lr*temp;
}
}
//调整sita_h
for(j=0;j<hidenode;j++)
{
temp=0;
for(k=0;k<sample_num;k++)
{
temp-=delta_ih[k][j];
}
sita_h[j]+=0.005*temp;
}
//调整w_ho
for(i=0;i<hidenode;i++)
{
for(j=0;j<outputnode;j++)
{
temp = 0;
for (k=0;k<sample_num;k++)
{
temp+=delta_ho[k][j]*a[k][i];
}
w_ho[i][j]+=lr*temp;
}
}
//调整sita_o
for (i=0;i<outputnode;i++)
{
temp=0;
for(j=0;j<sample_num;j++)
{
temp-=delta_ho[j][i];
}
sita_o[i]+=0.005*temp;
}
if(totalerror<goal) break;
}
}
void test(double x0,double y0)
{
int flag;
int j,k;
double net_h[hidenode];
double net_o[outputnode];
double hide[hidenode];
double output[outputnode];
for(j=0;j<hidenode;j++)
{
net_h[j]=w_ih[0][j]*x0+w_ih[1][j]*y0-sita_h[j];
hide[j]=1/(1+exp(-net_h[j]));
}
for(k=0;k<outputnode;k++)
{
net_o[k]=0;
for(j=0;j<hidenode;j++)
{
net_o[k]+=w_ho[j][k]*hide[j];
}
net_o[k]-=sita_o[k];
output[k]=1/(1+exp(-net_o[k]));
}
if(output[0]>0.5) flag=1;
if(output[1]>0.5) flag=2;
if(output[2]>0.5) flag=3;
if(output[3]>0.5) flag=4;
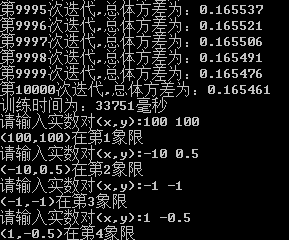
cout<<"("<<x0<<","<<y0<<")"<<"在第"<<flag<<"象限"<<endl;
}
int main()
{
init();
clock_t starttime=clock();
train();
clock_t endtime=clock();
cout<<"训练时间为："<<endtime-starttime<<"毫秒"<<endl;
while(1)
{
double a,b;
cout<<"请输入实数对(x,y):";
cin>>a>>b;
test(a,b);
}
return 0;
}
参考文献：
1. 《机器学习》Tom Mitchell著
2. 其他
如有任何问题，欢迎批评指正，谢谢！