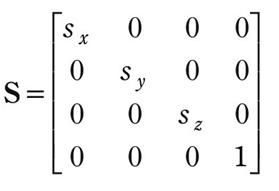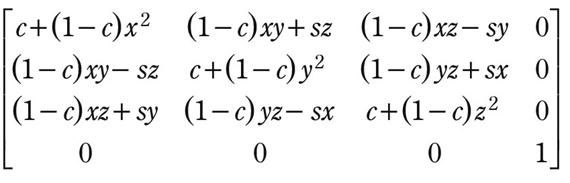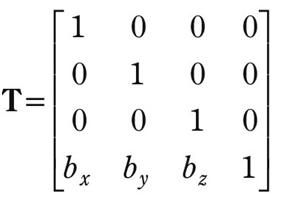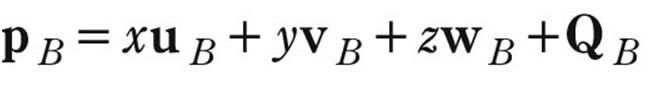D3D矢量运算

1. 向量和点

需要掌握的向量运算有：加，减，乘以实数，求长，求单位向量，点乘，×乘。更重要的是，要明确其物理意义，具体的就随便找本线性代数课本看好了。它在图形学中的碰撞处理、物理模拟等常见技术中占有极重要的地位。同时也要明白点和向量的关系，点表示位置，向量表示一个方向的运动。D3D中的向量封装在D3DVECTOR结构的各个子类中（注意，c++中的类和结构只有默认访问权限上的区别），其中包含了常用的向量计算函数。如，D3DXVECTOR3代表一个三维向量。

 

2. 矩阵

需要掌握矩阵的基本计算，特别是乘法。矩阵在图形学中，主要D3D用于通过代数思想来实现缩放、转动、移动（平移）等视觉上重要的图像行为。D3D中的矩阵封装在D3DMATRIX的子类中，和向量一样，D3D也为我们实现了大部分的矩阵计算。

 

3. 图形变换的基本原理

我们在学习线性代数的时候，已经对矩阵和向量计算方面了解的比较清楚，相信大家都做过那些恶心人的证明题（本人考研的时候，线性代数证明题悲剧。。。），不过这里，我们要讨论的时，这些基础理论是怎么和图形的变换实现结合起来的。

3.1 你需要首先知道的一些细节

在D3D编程中，我们使用4*4的矩阵来实现变换，什么意思呢，就是说，我们用一个1*4的矩阵来代表一个向量或者一个点，设为小v，另外有个矩阵M为4*4矩阵来代表某种图形变换（放大，缩小，旋转，etc），然后vM即为变换后的点或者向量。

这里有个小问题，我们用4*4的矩阵来表示变换，是数学上的需要，但事实上，在3D世界中，1*3的向量或者点足以表现现实世界的位置和移动，那最后那一个数字用来做什么呢。事实上，规定1*4的矩阵来表示向量或者点，是因为矩阵乘法的需要（不然无法做乘法了嘛），当然，咱不能浪费，因此我们做一下规定：

(x, y, z, 0) for vectors

(x, y, z, 1) for points

这个规定事实上很严密，两个点的差即为向量，而两个向量加减后仍为向量。

3.2 简单变换1—缩放

虽然建模的实现方法很多，主流的方法是用一个个三角形组成一个立体模型，但当我们在操作建模对象是，仍是通过微观上操作点来实现对整体对象的操作。可能我说的有些迷糊，先看下下面的矩阵（原谅我使用书里的图，实在懒得去整这些数学符号）：

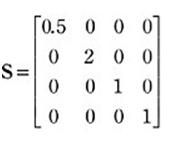
这个矩阵就是传中的缩放矩阵，一个向量或者点和他一乘，就实现缩放了。还是有些空洞吗，那我再拿一个书上的例子说明下：

设有

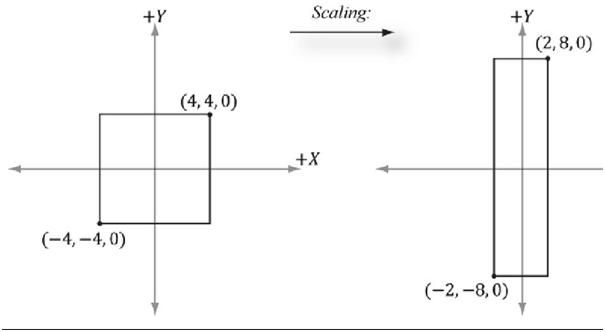
我们用两个点来表示一个矩形（2d的好理解些，3d其实一回事），分别为[4,4,4,1],[-4,-4,0,1]，然后让他们都去乘以S就实现了缩放，下面的示图演示了缩放过程：

3.3 简单变换2—旋转

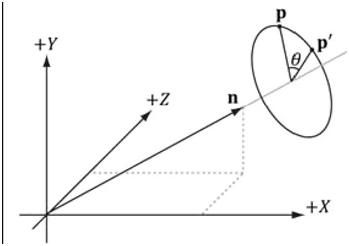
旋转相对来说要复杂些，首先看下面这张图，坐标系符合左手系：

我们要让p点围绕n轴旋转θ度到p'处，怎么实现呢？其实还是乘一个矩阵，这个称为旋转矩阵：

这个矩阵就没有缩放矩阵这么直观了，首先里面有很多参数，x,y,z是向量n的三维，即n=(x,y,z)。c = cos θ，s = sinθ。注意，在左手坐标系中，正角度对着n的方向的顺时针，即图中的θ是正角度。宏观的来说，也可以像上一节那样，用两点来表示一个正方形那样来模拟旋转的过程，这里就不详细说了。事实上，这个公式的推导我已经没啥印象了，如果有朋友对这块有兴趣，欢迎讨论哈。

3.4 简单变换3—移动（位移）

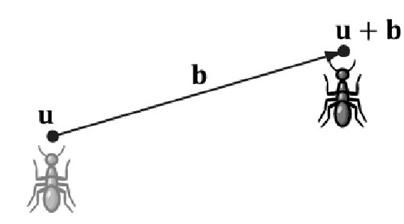
事实上，这个是最简单的，一个点加上一个向量即实现了一次位移，如下图：

点u加上向量b就运动到了另一点。当然，为了将这种变换和别的变换统一起来，我们还是需要给出位移矩阵：

这个应该一目了然了吧，偶就不多解释了。

3.5 图形变换的D3D实现

以上三个矩阵，能铭记于心当然最好，记不住，理解了，应该也ok，因为d3d已经讲其封装为一个个函数供我们使用（opengl等图形api也有类似函数）。考虑到效率，使用这些函数的时候都尽量传引用。

这里再提一下优化的问题，由于我们将每种变换都规格化到了4*4的矩阵，3D引擎可以比较方便的实现优化，如果需要连续多个变换，可以先将变化矩阵相乘，最后再乘以点或者向量，这个在由几十万个点组成的模型的时候，效果是相当好的。

 

4. 坐标系转换

坐标转换是什么，就是同一个点或者向量，在不同的坐标系中会有不同的位置，向量和点本身没变，但由于坐标系变换了，其也跟着变化。事实上，在3d游戏中，是非常重要的。我们经常以视角能否自由移动来判断一个游戏使用的是真3d还是假3d，而我们在转换视角时，相当于在变换坐标系，事实上物体的位置没变，只是在不同的坐标系中展示而已（我只是举个例子，事实上视角的转换实现要复杂的多）。

 

4.1 向量的坐标转换

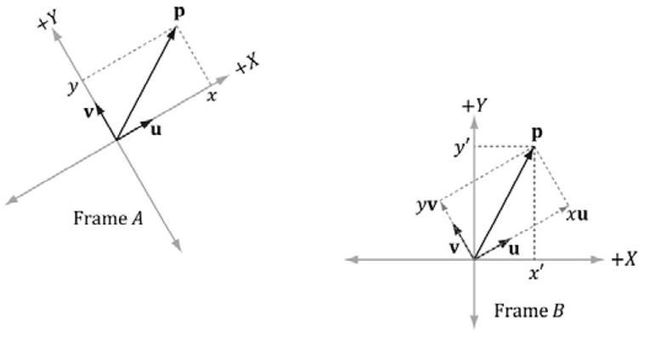
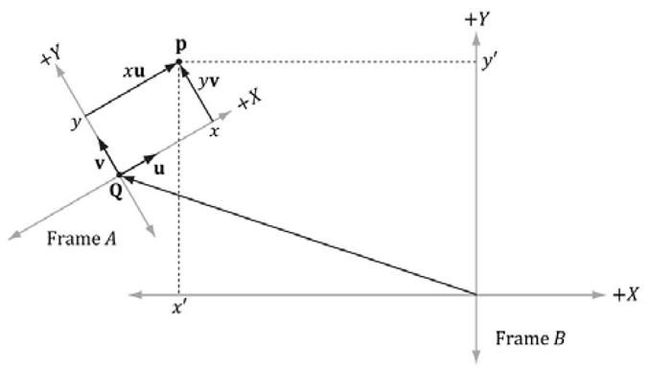
先考虑2D的情况，看下图：

向量p本身不变，但在不同的坐标系Frame A和Frame B下，它会有不同的坐标值，我们分别记为x,y与x',y'。

下面是推导过程：

在FrameA中，，u,v为Frame A中的单位向量。
转换到Frame B中，我们把u转换为Ub, V转换为Vb。
因此在Frame B中，我们得到等式。
推导到3D情况，我们有。

思想应该很明显了吧，我们不修改P点的x,y指，而是讲其单位向量替换为相关转换坐标系中的两个向量（仍然是一个单位的向量，但不是指向x和y轴的）。

 

4.2 点的坐标系转换

我们再来看点的情况，这个也很简单，公式为：

Z = 0的时候即为2D情况，下图可以说明推导过程：