卷积神经网络
深度神经网路已经在语音识别,图像识别等领域取得前所未有的成功。本人在多年之前也曾接触过神经网络。本系列文章主要记录自己对深度神经网络的一些学习心得。
第二篇,讲讲经典的卷积神经网络。我不打算详细描述卷积神经网络的生物学运行机理,因为网络上有太多的教程可以参考。这里,主要描述其数学上的计算过程,也就是如何自己编程去实现的问题。
1. 概述
回想一下BP神经网络。BP网络每一层节点是一个线性的一维排列状态,层与层的网络节点之间是全连接的。这样设想一下,如果BP网络中层与层之间的节点连接不再是全连接,而是局部连接的。这样,就是一种最简单的一维卷积网络。如果我们把上述这个思路扩展到二维,这就是我们在大多数参考资料上看到的卷积神经网络。具体参看下图:
上图左:全连接网络。如果我们有1000x1000像素的图像,有1百万个隐层神经元,每个隐层神经元都连接图像的每一个像素点,就有1000x1000x1000000=10^12个连接,也就是10^12个权值参数。
上图右:局部连接网络,每一个节点与上层节点同位置附件10x10的窗口相连接,则1百万个隐层神经元就只有100w乘以100,即10^8个参数。其权值连接个数比原来减少了四个数量级。
根据BP网络信号前向传递过程,我们可以很容易计算网络节点的输出。例如,对于上图中被标注为红色节点的净输入,就等于所有与红线相连接的上一层神经元节点值与红色线表示的权值之积的累加。这样的计算过程,很多书上称其为卷积。
事实上,对于数字滤波而言,其滤波器的系数通常是对称的。否则,卷积的计算需要先反向对折,然后进行乘累加的计算。上述神经网络权值满足对称吗?我想答案是否定的!所以,上述称其为卷积运算,显然是有失偏颇的。但这并不重要,仅仅是一个名词称谓而已。只是,搞信号处理的人,在初次接触卷积神经网络的时候,带来了一些理解上的误区。
卷积神经网络另外一个特性是权值共享。例如,就上面右边那幅图来说,权值共享,不是说,所有的红色线标注的连接权值相同。这一点,初学者容易产生误解。
上面描述的只是单层网络结构,前A&T Shannon Lab 的 Yann LeCun等人据此提出了基于卷积神经网络的一个文字识别系统 LeNet-5。该系统90年代就被用于银行手写数字的识别。
2. 文字识别系统LeNet-5
在经典的模式识别中,一般是事先提取特征。提取诸多特征后,要对这些特征进行相关性分析,找到最能代表字符的特征,去掉对分类无关和自相关的特征。然而,这些特征的提取太过依赖人的经验和主观意识,提取到的特征的不同对分类性能影响很大,甚至提取的特征的顺序也会影响最后的分类性能。同时,图像预处理的好坏也会影响到提取的特征。那么,如何把特征提取这一过程作为一个自适应、自学习的过程,通过机器学习找到分类性能最优的特征呢?
卷积神经元每一个隐层的单元提取图像局部特征,将其映射成一个平面,特征映射函数采用 sigmoid 函数作为卷积网络的激活函数,使得特征映射具有位移不变性。每个神经元与前一层的局部感受野相连。注意前面我们说了,不是局部连接的神经元权值相同,而是同一平面层的神经元权值相同,有相同程度的位移、旋转不变性。每个特征提取后都紧跟着一个用来求局部平均与二次提取的亚取样层。这种特有的两次特征提取结构使得网络对输入样本有较高的畸变容忍能力。也就是说,卷积神经网络通过局部感受野、共享权值和亚取样来保证图像对位移、缩放、扭曲的鲁棒性。
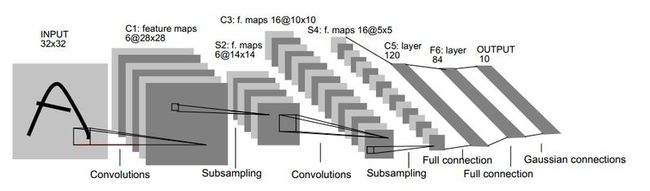
下面,有必要来解释下上面这个用于文字识别的LeNet-5深层卷积网络。
1. 输入图像是32x32的大小,局部滑动窗的大小是5x5的,由于不考虑对图像的边界进行拓展,则滑动窗将有28x28个不同的位置,也就是C1层的大小是28x28。这里设定有6个不同的C1层,每一个C1层内的权值是相同的。
2. S2层是一个下采样层。简单的说,由4个点下采样为1个点,也就是4个数的加权平均。但在LeNet-5系统,下采样层比较复杂,因为这4个加权系数也需要学习得到,这显然增加了模型的复杂度。在斯坦福关于深度学习的教程中,这个过程叫做Pool。
3. 根据对前面C1层同样的理解,我们很容易得到C3层的大小为10x10. 只不过,C3层的变成了16个10x10网络! 试想一下,如果S2层只有1个平面,那么由S2层得到C3就和由输入层得到C1层是完全一样的。但是,S2层由多层,那么,我们只需要按照一定的顺利组合这些层就可以了。具体的组合规则,在 LeNet-5 系统中给出了下面的表格:
简单的说,例如对于C3层第0张特征图,其每一个节点与S2层的第0张特征图,第1张特征图,第2张特征图,总共3个5x5个节点相连接。后面依次类推,C3层每一张特征映射图的权值是相同的。
4. S4 层是在C3层基础上下采样,前面已述。在后面的层由于每一层节点个数比较少,都是全连接层,这个比较简单,不再赘述。
3. 简化的LeNet-5系统
4. 卷积神经网络的实现问题