Leetcode | Trapping Rain Water

Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.

For example,
Given [0,1,0,2,1,0,1,3,2,1,2,1], return 6.

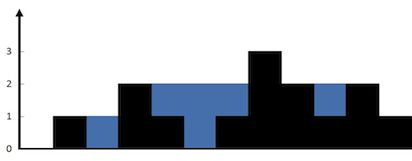
The above elevation map is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped. Thanks Marcos for contributing this image!

Method I

这道题用的和Largest Rectangle in Histogram类似的算法，都是用了一个栈。如果比栈顶小或者栈为空，就push进栈；如果比栈顶大，就计算围起来的面积。为了不重复计算面积，每次只计算，在栈顶以上，在栈顶的前一个数(pop之后的栈顶）和当前数围起来的长方形面积(Line 13)。

 1 class Solution {

 2 public:

 3     int trap(int A[], int n) {

 4         int sum = 0; 

 5         stack<int> st;

 6         

 7         for (int i = 0; i < n; ) {

 8             if (st.empty()) {

 9                 st.push(i++);

10             } else if (A[i] >= A[st.top()]) {

11                 int tmp = st.top();

12                 st.pop();

13                 if (!st.empty()) sum += (i - st.top() - 1) * (min(A[i], A[st.top()]) - A[tmp]);

14             } else {

15                 st.push(i++);

16             }

17         }

18         return sum;

19     }

20 };

Method II 

网上有另外一种算法，思路是算出每个位置可以存的雨量。就是把总雨量分摊到每个位置。当前位置的雨量由它的min(左边最大值,右边最大值)决定。照着思路重写了一遍。

 1 class Solution {

 2 public:

 3     int trap(int A[], int n) {

 4         if (n == 0) return 0;

 5         int sum = 0; 

 6         vector<int> lfmost(n, 0);

 7         

 8         lfmost[0] = A[0];

 9         for (int i = 1; i < n; ++i) {

10             lfmost[i] = lfmost[i - 1] > A[i - 1] ? lfmost[i - 1] : A[i - 1];

11         }

12         

13         int max = A[n - 1];

14         for (int j = n - 2; j >= 1; --j) {

15             if (A[j + 1] > max) max = A[j + 1];

16             int s = min(lfmost[j], max) - A[j];

17             if (s > 0) sum += s;

18         }

19         return sum;

20     }

21 };