POJ 3921（费用流+拆点）

题目大意：
一个有向图有N个点,M条边。现在要求删掉最少的点,使得不存在从1号点到N号点的长度<=K的路径（不能直接删掉1号点或N号点）。求最少删除多少点。

PS：边是有向的

 

思路：费用流+拆点（话说dfs貌似也能过，毕竟点那么少）
把每个点拆成两个点，a1和a2，中间连一条容量为1，费用为0的边（注意起点和终点的处理）
对于每一条数据中的有向边a-->b，连一条a2-->b1的容量为INF，费用为1的边

剩下的就是跑费用流啦~当最短路大于K停止

 

PS：这个算法是错的，请看这组数据

10 11 5

1 2 

2 3

3 4

4 5

5 10

2 9

1 6

6 7

7 8

8 9

9 10

图：

 

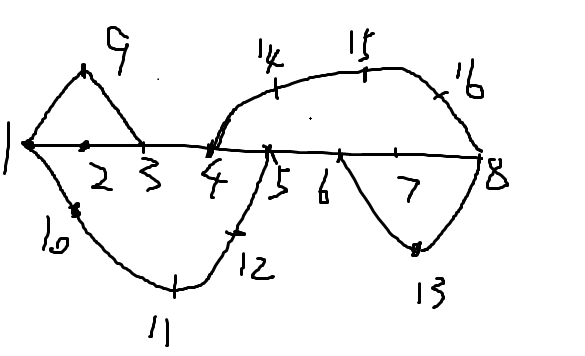
 正解应该是迭代加深搜索吧。不知道还有哪位神犇有神级的思路！

 

View Code

 1 #include <cstdio>

 2 #include <cstdlib>

 3 #include <cstring>

 4 #define N 200

 5 #define M 500000

 6 #define INF 100000000

 7 using namespace std;

 8 int head[N],next[M],len[M],w[M],to[M],cnt,n,m,k,S,T,dis[N],q[M<<4],pre[M];

 9 bool vis[N];

10 void add(int u,int v,int c,int wp)

11 {

12     to[cnt]=v; len[cnt]=c; w[cnt]=wp; next[cnt]=head[u]; head[u]=cnt++;

13     to[cnt]=u; len[cnt]=0; w[cnt]=-wp; next[cnt]=head[v]; head[v]=cnt++;

14 }

15 void read()

16 {

17     memset(head,-1,sizeof head);cnt=0;

18     for(int i=2;i<n;i++) add(i,i+n,1,0);

19     add(1,1+n,INF,0); add(n,n+n,INF,0);//拆点 

20     for(int i=1,a,b;i<=m;i++)

21     {

22         scanf("%d%d",&a,&b);

23         add(a+n,b,INF,1);

24     }

25     S=1; T=n+n;

26 }

27 bool spfa()

28 {

29     for(int i=0;i<=T;i++) dis[i]=INF;

30     int h=1,t=2,sta;

31     q[1]=S; vis[S]=true; dis[S]=0; pre[S]=-1;

32     while(h<t)

33     {

34         sta=q[h++];

35         vis[sta]=false;

36         for(int i=head[sta];~i;i=next[i])

37             if(len[i]>0&&dis[to[i]]>dis[sta]+w[i])

38             {

39                 dis[to[i]]=dis[sta]+w[i];

40                 pre[to[i]]=i;

41                 if(!vis[to[i]])

42                 {

43                     vis[to[i]]=true;

44                     q[t++]=to[i];

45                 }

46             }

47     }

48     return dis[T]!=INF;

49 }

50 void go()

51 {

52     int cs=0;

53     while(spfa())

54     {

55         if(dis[T]>k) break;

56         cs++;//printf("%d\n",cs);

57         for(int i=T,tmp;i!=S;i=to[tmp^1])

58         {

59             //printf("%d\n",i);

60             tmp=pre[i];

61             len[tmp]-=1;

62             len[tmp^1]+=1;

63         }

64     }

65     printf("%d\n",cs);

66 }

67 int main()

68 {

69     while(scanf("%d%d%d",&n,&m,&k),n||m||k)

70     {

71         read();

72         go();

73     }

74     return 0;

75 }

 

 

后记：这个才是假期最后一篇。