经典算法题每日演练——第九题 优先队列
前端时间玩小爬虫的时候,我把url都是放在内存队列里面的,有时我们在抓取url的时候,通过LCS之类的相似度比较,发现某些url是很重要的,
需要后端解析服务器优先处理,针对这种优先级比较大的url,普通的队列还是苦逼的在做FIFO操作,现在我们的需求就是优先级大的优先服务,要做
优先队列,非堆莫属。
一:堆结构
1:性质
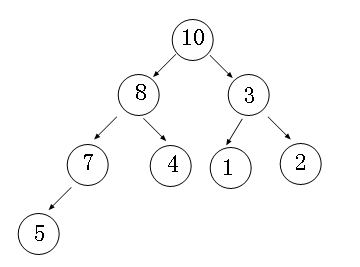
堆是一种很松散的序结构树,只保存了父节点和孩子节点的大小关系,并不规定左右孩子的大小,不像排序树那样严格,又因为堆是一种完全二叉
树,设节点为i,则i/2是i的父节点,2i是i的左孩子,2i+1是i的右孩子,所以在实现方式上可以采用轻量级的数组。
2:用途
如果大家玩过微软的MSMQ的话,我们发现它其实也是一个优先队列,还有刚才说的抓取url,不过很遗憾,为什么.net类库中没有优先队列,而java1.5
中就已经支持了。
3:实现
<1>堆结构节点定义:
我们在每个节点上定义一个level,表示该节点的优先级,也是构建堆时采取的依据。
1 /// <summary> 2 /// 定义一个数组来存放节点 3 /// </summary> 4 private List<HeapNode> nodeList = new List<HeapNode>(); 5 6 #region 堆节点定义 7 /// <summary> 8 /// 堆节点定义 9 /// </summary> 10 public class HeapNode 11 { 12 /// <summary> 13 /// 实体数据 14 /// </summary> 15 public T t { get; set; } 16 17 /// <summary> 18 /// 优先级别 1-10个级别 (优先级别递增) 19 /// </summary> 20 public int level { get; set; } 21 22 public HeapNode(T t, int level) 23 { 24 this.t = t; 25 this.level = level; 26 } 27 28 public HeapNode() { } 29 } 30 #endregion
<2> 入队操作
入队操作时我们要注意几个问题:
①:完全二叉树的构建操作是“从上到下,从左到右”的形式,所以入队的节点是放在数组的最后,也就是树中叶子层的有序最右边空位。
②:当节点插入到最后时,有可能破坏了堆的性质,此时我们要进行“上滤操作”,当然时间复杂度为O(lgN)。
当我将节点“20”插入到堆尾的时候,此时破坏了堆的性质,从图中我们可以清楚的看到节点“20”的整个上滤过程,有意思吧,还有一点
就是:获取插入节点的父亲节点的算法是:parent=list.count/2-1。这也得益于完全二叉树的特性。
1 #region 添加操作 2 /// <summary> 3 /// 添加操作 4 /// </summary> 5 public void Eequeue(T t, int level = 1) 6 { 7 //将当前节点追加到堆尾 8 nodeList.Add(new HeapNode(t, level)); 9 10 //如果只有一个节点,则不需要进行筛操作 11 if (nodeList.Count == 1) 12 return; 13 14 //获取最后一个非叶子节点 15 int parent = nodeList.Count / 2 - 1; 16 17 //堆调整 18 UpHeapAdjust(nodeList, parent); 19 } 20 #endregion 21 22 #region 对堆进行上滤操作,使得满足堆性质 23 /// <summary> 24 /// 对堆进行上滤操作,使得满足堆性质 25 /// </summary> 26 /// <param name="nodeList"></param> 27 /// <param name="index">非叶子节点的之后指针(这里要注意:我们 28 /// 的筛操作时针对非叶节点的) 29 /// </param> 30 public void UpHeapAdjust(List<HeapNode> nodeList, int parent) 31 { 32 while (parent >= 0) 33 { 34 //当前index节点的左孩子 35 var left = 2 * parent + 1; 36 37 //当前index节点的右孩子 38 var right = left + 1; 39 40 //parent子节点中最大的孩子节点,方便于parent进行比较 41 //默认为left节点 42 var max = left; 43 44 //判断当前节点是否有右孩子 45 if (right < nodeList.Count) 46 { 47 //判断parent要比较的最大子节点 48 max = nodeList[left].level < nodeList[right].level ? right : left; 49 } 50 51 //如果parent节点小于它的某个子节点的话,此时筛操作 52 if (nodeList[parent].level < nodeList[max].level) 53 { 54 //子节点和父节点进行交换操作 55 var temp = nodeList[parent]; 56 nodeList[parent] = nodeList[max]; 57 nodeList[max] = temp; 58 59 //继续进行更上一层的过滤 60 parent = (int)Math.Ceiling(parent / 2d) - 1; 61 } 62 else 63 { 64 break; 65 } 66 } 67 } 68 #endregion
<3> 出队操作
从图中我们可以看出,优先级最大的节点会在一阵痉挛后上升到堆顶,出队操作时,我们采取的方案是:弹出堆顶元素,然后将叶子层中
的最右子节点赋给堆顶,同样这时也会可能存在破坏堆的性质,最后我们要被迫进行下滤操作。
我图中可以看出:首先将堆顶20弹出,然后将7赋给堆顶,此时堆性质遭到破坏,最后我们清楚的看到节点7的下滤过程,从摊还分析的角度上
来说,下滤的层数不超过2-3层,所以整体上来说出队的时间复杂度为一个常量O(1)。
1 #region 优先队列的出队操作 2 /// <summary> 3 /// 优先队列的出队操作 4 /// </summary> 5 /// <returns></returns> 6 public HeapNode Dequeue() 7 { 8 if (nodeList.Count == 0) 9 return null; 10 11 //出队列操作,弹出数据头元素 12 var pop = nodeList[0]; 13 14 //用尾元素填充头元素 15 nodeList[0] = nodeList[nodeList.Count - 1]; 16 17 //删除尾节点 18 nodeList.RemoveAt(nodeList.Count - 1); 19 20 //然后从根节点下滤堆 21 DownHeapAdjust(nodeList, 0); 22 23 return pop; 24 } 25 #endregion 26 27 #region 对堆进行下滤操作,使得满足堆性质 28 /// <summary> 29 /// 对堆进行下滤操作,使得满足堆性质 30 /// </summary> 31 /// <param name="nodeList"></param> 32 /// <param name="index">非叶子节点的之后指针(这里要注意:我们 33 /// 的筛操作时针对非叶节点的) 34 /// </param> 35 public void DownHeapAdjust(List<HeapNode> nodeList, int parent) 36 { 37 while (2 * parent + 1 < nodeList.Count) 38 { 39 //当前index节点的左孩子 40 var left = 2 * parent + 1; 41 42 //当前index节点的右孩子 43 var right = left + 1; 44 45 //parent子节点中最大的孩子节点,方便于parent进行比较 46 //默认为left节点 47 var max = left; 48 49 //判断当前节点是否有右孩子 50 if (right < nodeList.Count) 51 { 52 //判断parent要比较的最大子节点 53 max = nodeList[left].level < nodeList[right].level ? right : left; 54 } 55 56 //如果parent节点小于它的某个子节点的话,此时筛操作 57 if (nodeList[parent].level < nodeList[max].level) 58 { 59 //子节点和父节点进行交换操作 60 var temp = nodeList[parent]; 61 nodeList[parent] = nodeList[max]; 62 nodeList[max] = temp; 63 64 //继续进行更下一层的过滤 65 parent = max; 66 } 67 else 68 { 69 break; 70 } 71 } 72 } 73 #endregion
最后我还扩展了一个弹出并下降节点优先级的方法,好吧,这个方法大家自己琢磨琢磨,很有意思的,实际应用中使用到了。
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Diagnostics;
using System.Threading;
using System.IO;
namespace ConsoleApplication2
{
public class Program
{
public static void Main()
{
PriorityQueue<Url> heap = new PriorityQueue<Url>();
//随机插入20个节点
for (int i = 1; i < 20; i++)
{
var rand = new Random().Next(1, 20);
Thread.Sleep(10);
heap.Eequeue(new Url() { Data = "test" + i }, i);
}
while (true)
{
var node = heap.Dequeue();
if (node == null)
break;
Console.WriteLine("当前url的优先级为:{0},数据为:{1}", node.level, node.t.Data);
}
Console.Read();
}
}
#region 定义一个实体
/// <summary>
/// 定义一个实体
/// </summary>
public class Url
{
public string Data { get; set; }
}
#endregion
public class PriorityQueue<T> where T : class
{
/// <summary>
/// 定义一个数组来存放节点
/// </summary>
private List<HeapNode> nodeList = new List<HeapNode>();
#region 堆节点定义
/// <summary>
/// 堆节点定义
/// </summary>
public class HeapNode
{
/// <summary>
/// 实体数据
/// </summary>
public T t { get; set; }
/// <summary>
/// 优先级别 1-10个级别 (优先级别递增)
/// </summary>
public int level { get; set; }
public HeapNode(T t, int level)
{
this.t = t;
this.level = level;
}
public HeapNode() { }
}
#endregion
#region 添加操作
/// <summary>
/// 添加操作
/// </summary>
public void Eequeue(T t, int level = 1)
{
//将当前节点追加到堆尾
nodeList.Add(new HeapNode(t, level));
//如果只有一个节点,则不需要进行筛操作
if (nodeList.Count == 1)
return;
//获取最后一个非叶子节点
int parent = nodeList.Count / 2 - 1;
//堆调整
UpHeapAdjust(nodeList, parent);
}
#endregion
#region 对堆进行上滤操作,使得满足堆性质
/// <summary>
/// 对堆进行上滤操作,使得满足堆性质
/// </summary>
/// <param name="nodeList"></param>
/// <param name="index">非叶子节点的之后指针(这里要注意:我们
/// 的筛操作时针对非叶节点的)
/// </param>
public void UpHeapAdjust(List<HeapNode> nodeList, int parent)
{
while (parent >= 0)
{
//当前index节点的左孩子
var left = 2 * parent + 1;
//当前index节点的右孩子
var right = left + 1;
//parent子节点中最大的孩子节点,方便于parent进行比较
//默认为left节点
var max = left;
//判断当前节点是否有右孩子
if (right < nodeList.Count)
{
//判断parent要比较的最大子节点
max = nodeList[left].level < nodeList[right].level ? right : left;
}
//如果parent节点小于它的某个子节点的话,此时筛操作
if (nodeList[parent].level < nodeList[max].level)
{
//子节点和父节点进行交换操作
var temp = nodeList[parent];
nodeList[parent] = nodeList[max];
nodeList[max] = temp;
//继续进行更上一层的过滤
parent = (int)Math.Ceiling(parent / 2d) - 1;
}
else
{
break;
}
}
}
#endregion
#region 优先队列的出队操作
/// <summary>
/// 优先队列的出队操作
/// </summary>
/// <returns></returns>
public HeapNode Dequeue()
{
if (nodeList.Count == 0)
return null;
//出队列操作,弹出数据头元素
var pop = nodeList[0];
//用尾元素填充头元素
nodeList[0] = nodeList[nodeList.Count - 1];
//删除尾节点
nodeList.RemoveAt(nodeList.Count - 1);
//然后从根节点下滤堆
DownHeapAdjust(nodeList, 0);
return pop;
}
#endregion
#region 对堆进行下滤操作,使得满足堆性质
/// <summary>
/// 对堆进行下滤操作,使得满足堆性质
/// </summary>
/// <param name="nodeList"></param>
/// <param name="index">非叶子节点的之后指针(这里要注意:我们
/// 的筛操作时针对非叶节点的)
/// </param>
public void DownHeapAdjust(List<HeapNode> nodeList, int parent)
{
while (2 * parent + 1 < nodeList.Count)
{
//当前index节点的左孩子
var left = 2 * parent + 1;
//当前index节点的右孩子
var right = left + 1;
//parent子节点中最大的孩子节点,方便于parent进行比较
//默认为left节点
var max = left;
//判断当前节点是否有右孩子
if (right < nodeList.Count)
{
//判断parent要比较的最大子节点
max = nodeList[left].level < nodeList[right].level ? right : left;
}
//如果parent节点小于它的某个子节点的话,此时筛操作
if (nodeList[parent].level < nodeList[max].level)
{
//子节点和父节点进行交换操作
var temp = nodeList[parent];
nodeList[parent] = nodeList[max];
nodeList[max] = temp;
//继续进行更下一层的过滤
parent = max;
}
else
{
break;
}
}
}
#endregion
#region 获取元素并下降到指定的level级别
/// <summary>
/// 获取元素并下降到指定的level级别
/// </summary>
/// <returns></returns>
public HeapNode GetAndDownPriority(int level)
{
if (nodeList.Count == 0)
return null;
//获取头元素
var pop = nodeList[0];
//设置指定优先级(如果为 MinValue 则为 -- 操作)
nodeList[0].level = level == int.MinValue ? --nodeList[0].level : level;
//下滤堆
DownHeapAdjust(nodeList, 0);
return nodeList[0];
}
#endregion
#region 获取元素并下降优先级
/// <summary>
/// 获取元素并下降优先级
/// </summary>
/// <returns></returns>
public HeapNode GetAndDownPriority()
{
//下降一个优先级
return GetAndDownPriority(int.MinValue);
}
#endregion
}
}