多维算法思考(三):AB组合问题
多维算法思考(三):AB组合问题
题目:x个A,y个B可以组合成多少个不同排列的问题。
首先,我们用数学的方式思考,这个问题属于《组合数学》的问题,我们的第一种方法可以用组合思路来求解。
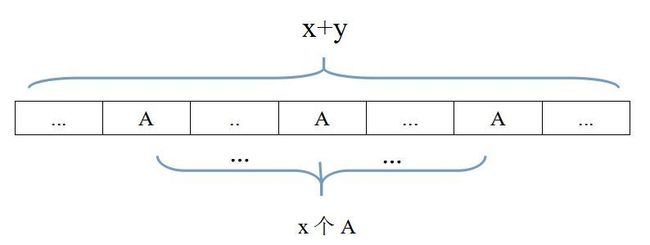
也就是说在x+y个单元格中随机选出x个单元格用来存放A,那么其他的也就自然存放B,所以共有 种不同的排列,例如当x=3,y=2时,可组成10种不同的排列。
种不同的排列,例如当x=3,y=2时,可组成10种不同的排列。
这种方法虽好,但不直观。如果我们要列出所有的AB组合,这种方法显然不容易办到,这时我们可以用另一种方法来求解。利用递归的思想。我们用f(x,y)表示x个A,y个B可以组合成的不同排列数,则当第一个是A时,共有f(x-1,y)种不同排列数,当第一个是B时,共有f(x,y-1)种不同排列数。所以f(x,y)=f(x-1,y)+f(x,y-1)。
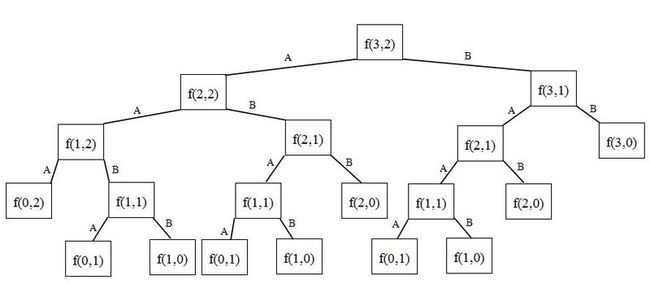
也许有人会问,这样一个递归式子,我们不是一样看不出来AB组合吗?确实,从表面看,我们也不能直观的列出AB组合。这是我们需要对其变通一下,将它转换成树状图。下面我们还是以x=3,y=2为例:
x每减一,树枝上就会多一A;y每减一,树枝上就会多一B。若x或y为0,则结束,剩下的数字即为B或A的个数。上述AB组合从左到右依次为AAABB--AABAB--AABBA--ABAAB--ABABA--ABBAA--BAAAB--BAABA--BABAA--BBAAA共可组成10种不同的排列。
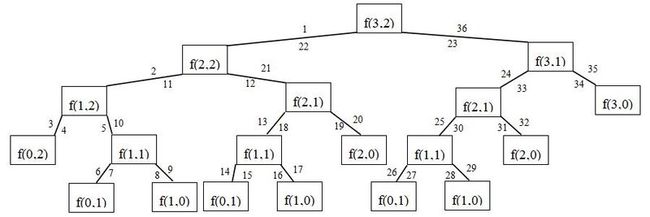
下面我们用C语言来实现上述递归算法。(递归执行顺序图如下)
算法思路:原理同上述树状执行图。我们先设两个全局变量p,q,初始值p=x,q=y。通过每一次x与p,y与q的大小比较来判断执行的流程。
当x=0或y=0时结束。用数组a[5]来记录执行过程中AB的顺序。
完整算法:
//x个A,y个B可以组合成多少个不同排列的问题 #include<stdio.h> #define x 4 #define y 2 int p=x,q=y,k=0; char a[5]; int fun(int m,int n) { if(m<p) { a[k++]='A'; p=m; q=n; if(m==0) { for(int j=0;j<k;j++) printf("%c",a[j]); for(int i=0;i<n;i++) printf("B"); printf("\n"); k--; p++; return 1; } } else if(m>p) { for(int i=p;i<m;i++) k--; p=m; if(q==n) { q++; k--; } } if(n<q) { a[k++]='B'; p=m; q=n; if(n==0) { for(int j=0;j<k;j++) printf("%c",a[j]); for(int i=0;i<m;i++) printf("A"); printf("\n"); k--; q++; return 1; } } else if(n>q) { for(int i=q;i<n;i++) k--; q=n; if(p==m) { p++; k--; } } return fun(m-1,n)+fun(m,n-1); } void main() { printf("\n%d个A,%d个B可组成%d种不同的排列\n",x,y,fun(x,y)); }
执行效果图: