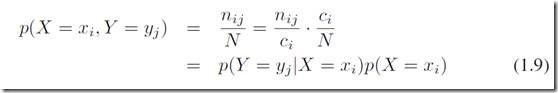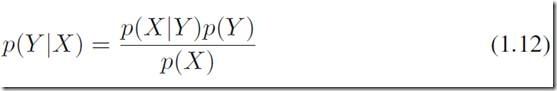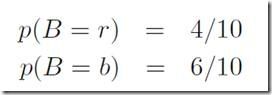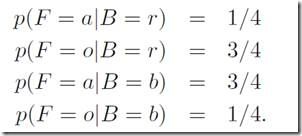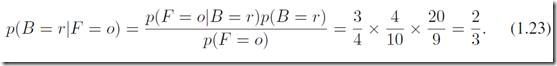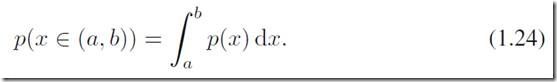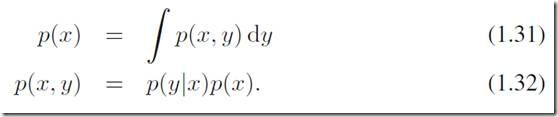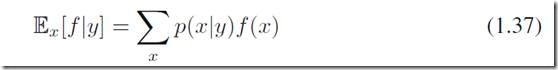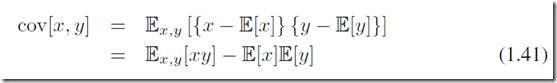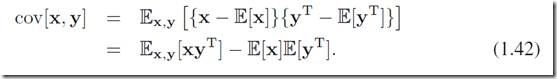今天开始学Pattern Recognition and Machine Learning (PRML)书，章节1.2，Probability Theory （上）

原创书写，转载请注明此文出自：http://blog.csdn.net/xbinworld，Bin的专栏

 

Pattern Recognition and Machine Learning (PRML)书，章节1.2，Probability Theory （上）

这一节是浓缩了整本书关于概率论的精华，突出一个不确定性（uncertainty）的理解。我看的比较慢，是想要细扣一下，而且写blog码字也很慢，不过我想留下点痕迹所以会写下去。前面几节其实很重要，所以单独一节甚至半节写一个blog，后面如果一个章节在讨论一个topic我可能就会一个章节一个blog，比如第九章讲EM算法，我应该就用一个blog带过。

(入门而已，高手一笑而过吧~。~)

对于书中的公式如果重要我都会推导一下，然后用黄色表示一下，以后的章节也是如此。如果大家也看PRML书建议也自己推几个公式，加深理解。如果出现“注”，就是我自己加的描述。

 

首先从一个例子说起：有两个盒子，一个红色盒子里面有2个苹果（绿）+6个桔子（黄），一个蓝色盒子里面有3个苹果+1个桔子，具体可以见图1.9。随机挑选一个盒子，然后从盒子里随机拿出一个水果，观察是什么后放回原处，重复这个过程很多次。

我们定义挑选红色盒子的次数为总次数的40%，挑选蓝色盒子的次数为60%。

在这个例子中，盒子的颜色是一个随机变量，我们称之为B，它有两个取值r（red）和b（blue）；水果也是一个随机变量，称之为F，它的取值是a（apple）和o（orange）。

首先从频次的角度理解概率，选择红/蓝盒子的概率分别为：

注：概率必须在[0，1]范围内，且覆盖所有可能的互斥事件的概率和为1。

 

我们现在可以问类似这样的问题：（1）一次挑选得到苹果的概率是多少？（2）如果我们得到的是桔子，那么这一次挑选的是红盒子的概率是多少？

 

 

=============================================华丽的分割线==========================================================

在解决上述问题前我们先跳出这个例子，来考虑更一般的情况：见图1.10

 

对两个随机变量的大量重复实验，把得到（xi, yi）的结果次数记录到n_ij中，图中一列之和表示为ci（表示所有出现xi的总次数），一行之和为rj，为出现yj的总次数。得到X=xi和Y=yi的联合概率：

 

以及X=xi的边缘概率：

 

还可以得到条件概率，给定xi得到yj的概率：

通过以上推导，我们可以得到下面的关系：

 

上面的（1.7）式子叫做加法规则sum rule，（1.9）叫做乘法规则product rule， 是概率论中最基本的两个规则了：

注：这两个rule几乎是最重要的方法了。

通过这两个规则可以得到在机器学习中非常重要的贝叶斯理论：

其中P（X）可以对所有的Y展开：

可以理解为normalization，使得（1.12）左边的条件概率在所有的Y取值下，概率之和为1。

 

=============================================华丽的分割线============================================================

 

 

好了，现在跳回到前面的两个盒子的例子，（在下面的书写中我们会强调一下随机变量（大写字母）以及它们的实例（小写字母），后面可能就会写的简略一些）

这几个概率表达式都是直接得到的，题目中给了，比如第三条：盒子为红色情况下，抽到水果为苹果的概率为1/4。 且满足，即同一条件下所有可能性之和为1。OK, 现在我们可以回答“抽到苹果的概率”这个问题了:

即穷举所有盒子的可能，以及每一种盒子下抽到苹果的概率之和。对应的，抽到桔子的概率就是p(F=o) = 1- 11/20 = 9/20。

好，现在回答第二个问题：如果我们得到的是桔子，那么这一次挑选的是红盒子的概率是多少？

通过贝叶斯公式：

答案通过贝叶斯公式很容易得到，而我们所需的信息都可以从前面的基本信息中得到。在这个例子中，我们已经设计到很多概念，比如对盒子的选取有一个预估，也就是P(B)，我们称之为先验概率，因为它是在我们观测抽取结果之前就已知了的（决定了的）；

然后我们的第二个问题，已知抽到是桔子的情况下求盒子红色的概率，其实就是估计盒子为红色的后验概率，因为是在我们观察到随机变量F之后得到的估计。由此可见当我们有一定的观察值的时候我们就不能从直观的理解去判断一个事件，比如先验告诉我们说有60%的可能是选取蓝盒子，但式子是（1.23）说明在有观察o的情况下，红盒子的概率有2/3，比蓝盒子大多了。

还要介绍一下两个随机变量的边缘分布的乘积等于他们的联合分布，即p(X,Y) = p(X)P(Y)，那么这两个随机变量相互独立，也有p(Y|X) = p(Y)。

 

 

1.2.1 概率密度

前面介绍都是从离散变量的角度，我们需要重新考虑连续变量的概率定义。

如果一个实数连续变量，其落在区间的概率是，当时，那么小p(x)就称之为x的概率密度。概率定义成：

注：这里都用小p来表示容易混淆，前面的p是代表概率，后面p（x）是概率密度。

（连续变量就没有x为某一具体值的概率定义了，因为有无穷的取值，都是说落在一个区段内的概率）

累计分布函数（cumulative distribution）的定义是x处在区间的概率：

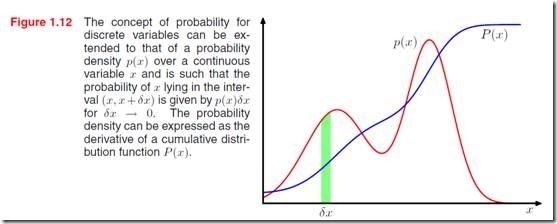
满足P’(x) = p(x)。在图1.12中我们绘制了概率密度小p和累计分布函数大P，绿色的面积是落在小区间内的概率。

前面讨论过的sum rule 和product rule在连续变量情况下也适用：

 

 

 

 

1.2.2 期望和方差

期望：一个函数f(x) 在一个概率分布p(x)下的平均取值就是f(x)的期望，定义为：

对于离散情况而言，期望就是一个所有可能值的加权和。对于连续变量就用对应的积分形式：

注：这里两个小p有不同，上面在离散情况下已经是理解成概率了，而下面（1.34）中小p是概率密度。

对期望的一种直观估计是所有观察点的平均：

当N趋于无穷大时，取等号。这样的平均值我们是经常用到的。

如果f有多个变量，我们一般会用下标来表示是针对哪一个变量的分布（变化）考虑的，比如

就是说f的关于变量x的期望，事实上，上式是一个以y为变量的函数。类似的，我们也可用定义条件期望：

方差：方差可以估计一个函数f在他的期望附近变化的剧烈程度，定义为

如果考虑变量x本身，也可用x的方差：

注：（书里跳过了）这个等式实际上是从方差的定义推导出来的：

 

另外，对于两个随机变量我们定义协方差:

表示x，y一起变化的程度，如果x和y相互独立，那么协方差为0。可以看到单个变量的方差是协方差的特殊情况，x=y。

如果x和y表示的是两个向量（vector）变量，x和y是列向量，那么协方差是一个矩阵：

 

好了，期望和方差介绍到这里，这两个概念几乎贯穿机器学习的所有领域。今天先记录这一些吧，章节1.2确实很重要，这里只是上半部分，下半部分过几天整理了再放出吧。

 

吐槽一下，写了这么几页就花了2小时+（动作太慢？），主要是语句都是经过梳理的，虽然公式和图表都是copy的，但是依然要花不少时间，记下来我自己加深下印象也是有好处。

1.2的下半部分包括了贝叶斯定理和高斯分布的介绍，非常重要。基本上章节1.2组成了概率统计学习的基础内容，建议初学者好好理解下。