Machine Learning in Action(3) 朴素贝叶斯算法

       贝叶斯决策一直很有争议，今年是贝叶斯250周年，历经沉浮，今天它的应用又开始逐渐活跃，有兴趣的可以看看斯坦福Brad Efron大师对其的反思，两篇文章：“Bayes'Theorem in the 21st Century”和“A250-YEAR ARGUMENT:BELIEF, BEHAVIOR, AND THE BOOTSTRAP”。俺就不参合这事了，下面来看看朴素贝叶斯分类器。

        有时我们想知道给定一个样本时，它属于每个类别的概率是多少,即P(Ci|X),Ci表示类别，X表示测试样本，有了概率后我们可以选择最大的概率的类别。要求这个概率要用经典贝叶斯公式，如（公式一）所示：

 

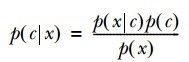
（公式一）

         （公式一）中的右边每项一般都是可以计算出的，例如（图一）中两个桶中分别装了黑色（Black）和灰色(Grey)的球。

 

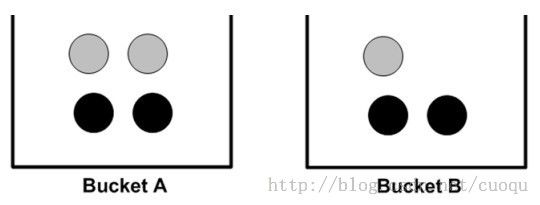
（图一）

        假设Bucket A和BucketB是类别，C1和C2，当给定一个球时，我们想判断它最可能从哪个桶里出来的，换句话说是什么类别？这就可以根据（公式一）来算，（公式一）的右边部分的每项都可以计算出来，比如P(gray|bucketA)=2/4，P(gray|bucketB)=1/3，更严格的计算方法是:

        P(gray|bucketB) = P(gray andbucketB)/P(bucketB),

        而P(gray and bucketB) = 1/7，P(bucketB)= 3/7

        那么P(gray|bucketB)=P(gray and bucketB)/ P(bucketB)=(1/7)/(3/7)=1/3

      这就是朴素贝叶斯的原理，根据后验概率来判断，选择P(Ci|X)最大的作为X的类别Ci,另外朴素贝叶斯只所以被称为朴素的原因是，它假设了特征之间都是独立的，如（图二）所示：

 

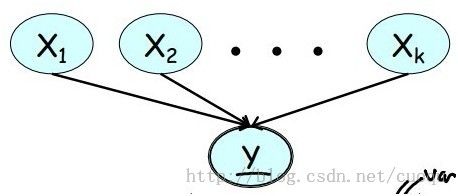
（图二）

       尽管这个假设很不严密，但是在实际应用中它仍然很有效果，比如文本分类，下面就来看下文本分类实战，判断聊天信息是否是辱骂（abusive）信息(也就是类别为两类，是否辱骂信息)，在此之前，先强调下，朴素贝叶斯的特征向量可以是多维的，上面的公式是一维的，二维的如（公式二）所示，都是相同的计算方法：

 

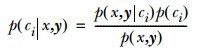
（公式二）

         对文本分类，首先的任务就是把文本转成数字向量，也就是提取特征。特征可以说某个关键字在文章中出现的次数(bag of words),比如垃圾邮件中经常出现“公司”，“酬宾”等字样，特征多样，可以根据所需自己建立特征。本例子中采用标记字（token）的方法，标记字可以是任何字符的组合，比如URL,单词，IP地址等，当然判断是否是辱骂信息大多数都是类似于单词的形式。下面来根据代码说下：

首先我们获取一些训练集：

 1 from numpy import *

 2 

 3 def loadDataSet():

 4     postingList=[['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],

 5                  ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],

 6                  ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],

 7                  ['stop', 'posting', 'stupid', 'worthless', 'garbage'],

 8                  ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],

 9                  ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]

10     classVec = [0,1,0,1,0,1]    #1 is abusive, 0 not

11     return postingList,classVec

 

        训练集是从聊天室里摘取的6句话，每句话都有一个标签0或者1，表示是否是辱骂信息（abusive or not abusive）。当然可以把每个消息看成是一个文档，只不过文档单词比这个多，但是一样的道理。接下来处理训练集，看看训练集有多少个不同的（唯一的）单词组成。代码如下：

1 def createVocabList(dataSet):

2     vocabSet = set([])  #create empty set

3     for document in dataSet:

4         vocabSet = vocabSet | set(document) #union of the two sets

5     return list(vocabSet)

 

        该函数返回一个由唯一单词组成的词汇表。接下来就是特征处理的关键步骤，同样先贴代码：

 

1 def setOfWords2Vec(vocabList, inputSet):

2     returnVec = [0]*len(vocabList)

3     for word in inputSet:

4         if word in vocabList:

5             returnVec[vocabList.index(word)] = 1

6         else: print "the word: %s is not in my Vocabulary!" % word

7     return returnVec

 

        这个函数功能：输入词汇表和消息，通过逐个索引词汇表，然后看消息中的是否有对应的字在词汇表中，如果有就标记1，没有就标记0，这样就把每条消息都转成了和词汇表一样长度的有0和1组成的特征向量，如（图三）所示：

（图三）

        有了特征向量，我们就可以训练朴素贝叶斯分类器了，其实就是计算（公式三）右边部分的三个概率，（公式三）如下：

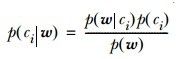
（公式三）

       其中w是特征向量。

代码如下：

 1 def trainNB0(trainMatrix,trainCategory):

 2     numTrainDocs = len(trainMatrix)

 3     numWords = len(trainMatrix[0])

 4     pAbusive = sum(trainCategory)/float(numTrainDocs)

 5     p0Num = ones(numWords); p1Num = ones(numWords)      #change to ones() 

 6     p0Denom = 2.0; p1Denom = 2.0                        #change to 2.0

 7     for i in range(numTrainDocs):

 8         if trainCategory[i] == 1:

 9             p1Num += trainMatrix[i]

10             p1Denom += sum(trainMatrix[i])

11         else:

12             p0Num += trainMatrix[i]

13             p0Denom += sum(trainMatrix[i])

14     p1Vect = log(p1Num/p1Denom)          #change to log()

15     p0Vect = log(p0Num/p0Denom)          #change to log()

16     return p0Vect,p1Vect,pAbusive

 

       上面的代码中输入的是特征向量组成的矩阵，和一个由标签组成的向量，其中pAbusive是类别概率P(ci)，因为只有两类，计算一类后，另外一类可以直接用1-p得出。接下来初始化计算p(wi|c1)和p(wi|c0)的分子和分母，这里惟一让人好奇的就是为什么分母p0Denom和p1Denom都初始化为2？这是因为在实际应用中，我们计算出了（公式三）右半部分的概率后，也就是p(wi|ci)后，注意wi表示消息中的一个字，接下来就是判断整条消息属于某个类别的概率，就要计算p(w0|1)p(w1|1)p(w2|1)的形式，这样如果某个wi为0，这样整个概率都为0，或者都很小连乘后会更小，甚至round off 0。这样就会影响判断，因此把他们转到对数空间中来做运算，对数在机器学习里经常用到，在保持单调的情况下避免因数值运算带来的歧义问题，而且对数可以把乘法转到加法运算，加速了运算。因此上面的代码中把所有的出现次数初始化为1，然后把分母初始为2，接着都是累加，在对数空间中从0还是1开始累加，最后比较大小不会受影响的。

最后贴出分类代码：

1 def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):

2     p1 = sum(vec2Classify * p1Vec) + log(pClass1)    #element-wise mult

3     p0 = sum(vec2Classify * p0Vec) + log(1.0 - pClass1)

4     if p1 > p0:

5         return 1

6     else: 

7         return 0

 

     分类代码也是在对数空间中计算的后验概率，然后通过比较大小来判断消息属于那一类。

总结：

       优点：对小量数据很有效，可以处理多类

       缺点：很依赖于数据的准备

朴素贝叶斯在概率图模型里被划为判别模型（Discriminative model)

以上内容来至群友博客:http://blog.csdn.net/marvin521

Ps:又见贝叶斯~之前，在machine learning for hacker里面有一篇关于Rstyle的贝叶斯，该算法简单高效，常用于spam检测和文本挖掘，像mahout里面的bayes就是为文本挖掘量身打造的。算法要求属性集是离散的，那么面对连续性的属性时，就要预先采用离散化了，可以结合连续型变量的分布用简单的分桶，最大描述准则(MDL)或者熵等等方法离散。