朴素贝页斯分类法 c++实现
朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法。对于搞机器学习的同学们来说,这是相对简单但效果较好的模型。
朴素贝叶斯方法的理论
设输入为n维特征向量X={x1,x2,...,xn},输出为类标记集合Y={c1,c2,...ck}。朴素贝叶斯法通过训练数据集学习联合概率分布P(X,Y),其中X是n维,Y是分类标记。有了模型P(X,Y),要预测一个特征向量的分类标记,则分别计算P(X,Y=c1),P(X,Y=c2),...P(X,Y=ck),选择取最大值的p(X,Y=cm),将cm作为X的分类标记。但对于模型P(X,Y)中的X是n维随机变量,若每一维特征取值最少有两个值,那么模型P(X,Y)参数量将是指数级的,这在特征维度较大的时候是不可行的。朴素贝叶斯法是引入条件独立性假设,由条件概率可得:
P(X=x,Y=ck)
=P(X(1)=x(1),X(2)=x(2),...X(n)=x(n)|Y=ck)*P(Y=ck)
(应用条件独立性假设)=P(X(1)=x(1)|Y=ck)*P(X(2)=x(2)|Y=ck)*...*P(X(n)=x(n)|Y=ck)*P(Y=ck)
即 =P(Y=ck)*∏i=1..nP(X(i)=x(i)|Y=ck)
条件独立性假设等于说用于分类的特征在类确定的情况下都是条件独立的。通过条件独立性假设,朴素贝叶斯法是模型变得简单,参数数量大大减少,但也牺牲一定的分类准确率。
朴素贝叶斯参数估计-极大似然估计
计算先验概率P(Y=ck)
P(Y=ck)=(∑i=1..nI(yi=ck))/N , k=1,2,...,K
其中I(yi=ck)为指示函数,当yi=ck时函数值等于1,否则为0。
计算条件概率P(X(j)=ajl|Y=ck)
P(X(j)=ajl|Y=ck)=(∑i=1..nI(xi(j)=ajl,yi=ck))/∑i=1..nI(yi=ck) ,j=1,2,,,n; l=1,2,Sj ;k=1,2,K
其中Sj是第j维特征的取值数。
由于计算条件概率可能会造成某个特征的计数为零,这样在预测分类的时候就会对有该特征的类计算值为0.为了避免这种情况,可采用拉普拉斯平滑处理。
预测分类
对给定的实例x=(x(1),x(2),...x(n))T,计算
P(Y=ck)*∏i=1..nP(X(i)=x(i)|Y=ck), k=1,2,...,K
然后根据上述K个结果,确定x的分类
y=argmax P(Y=ck)*∏i=1..n P(X(i)=x(i)|Y=ck)
例:
训练数据
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| x(1) | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 |
| x(2) | S | M | M | S | S | S | M | M | L | L | L | M | M | L | L |
| Y | -1 | -1 | 1 | 1 | -1 | -1 | -1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | -1 |
数据存储在文件中,每一行存储格式为<x(1) x(2) Y>,即特征1,特征2,分类属性以空格分隔。如下
1 S -1
1 M -1
1 M 1
1 S 1
1 S -1
2 S -1
2 M -1
2 M 1
2 L 1
2 L 1
3 L 1
3 M 1
3 M 1
3 L 1
3 L -1
代码如下:
/********************************************************************/
/*
朴素贝叶斯法
*/
/************************************************************************/
#include<iostream>
#include<string>
#include<fstream>
#include<sstream>
#include<vector>
#include<map>
#include<set>
using namespace std;
class naiveBayes{
public:
//载入数据并统计分量计数
void loadData(){
ifstream fin(dataFile.c_str());
if(!fin){
cout<<"数据文件打开失败"<<endl;
exit(0);
}
while(fin){
string line;
getline(fin,line);
if(line.size()>1){
stringstream sin(line);
string s[2];
int c;
sin>>s[0]>>s[1]>>c;
//cout<<s1<<" "<<s2<<" "<<c<<endl;
dataSize++;
if(ym.count(c)>0){
ym[c]++;
}else{
ym[c]=1;
}
for(int i=0;i<2;i++){
if(feam.count(s[i])>0){
if(feam[s[i]].count(c)>0){
feam[s[i]][c]++;
}else{
feam[s[i]][c]=1;
}
}else{
map<int,int> mt;
mt[c]=1;
feam[s[i]]=mt;
}
}
}
}
}
//显示map模型
void dispModel(){
cout<<"训练数据总数"<<endl;
cout<<dataSize<<endl;
cout<<"分类统计计数"<<endl;
for(map<int,int>::iterator mi=ym.begin();mi!=ym.end();mi++){
cout<<mi->first<<" "<<mi->second<<endl;
}
cout<<"特征统计计数:"<<endl;
for(map<string, map<int,int> >::iterator mi=feam.begin();mi!=feam.end();mi++){
cout<<mi->first<<": ";
for(map<int,int>::iterator ii=mi->second.begin();ii!=mi->second.end();ii++){
cout<<"<"<<ii->first<<" "<<ii->second<<"> ";
}
cout<<endl;
}
}
//预测分类
void predictive(){
string x1,x2;
cout<<"请输入测试数据(包括两维特征,第一维取值<1,2,3>;第二维取值<S,M,L>)"<<endl;
string a1[]={"1","2","3"};
string a2[]={"M","S","L"};
set<string> a1set(a1,a1+3);
set<string> a2set(a2,a2+3);
while(cin>>x1>>x2){
if(a1set.count(x1)>0&&a2set.count(x2)>0){
double py1=(double(ym[-1])/dataSize)*(double(feam[x1][-1])/ym[-1])*(double(feam[x2][-1])/ym[-1]);
double py2=(double(ym[1])/dataSize)*(double(feam[x1][1])/ym[1])*(double(feam[x2][1])/ym[1]);
cout<<"y=-1的得分为"<<py1<<endl;
cout<<"y=1的得分为"<<py2<<endl;
cout<<"<"<<x1<<","<<x2<<">"<<"所属分类为:";
if(py1>py2){
cout<<"-1";
}else{
cout<<"1";
}
cout<<endl;
cout<<endl;
cout<<"继续测试(ctrl+Z结束)"<<endl;
}else{
cout<<"输入特征为:第一维取值<1,2,3>;第二维取值<S,M,L>,空格分隔。输入有误,请重新输入"<<endl;
}
}
}
naiveBayes(string df="data.txt"):dataFile(df),dataSize(0){
}
private:
string dataFile;
int dataSize;
//分类->计数
map<int,int> ym;
//分类->( 特征->计数 )
map<string, map<int,int> >feam;
};
int main(){
naiveBayes nb;
nb.loadData();
nb.dispModel();
nb.predictive();
system("pause");
return 0;
}
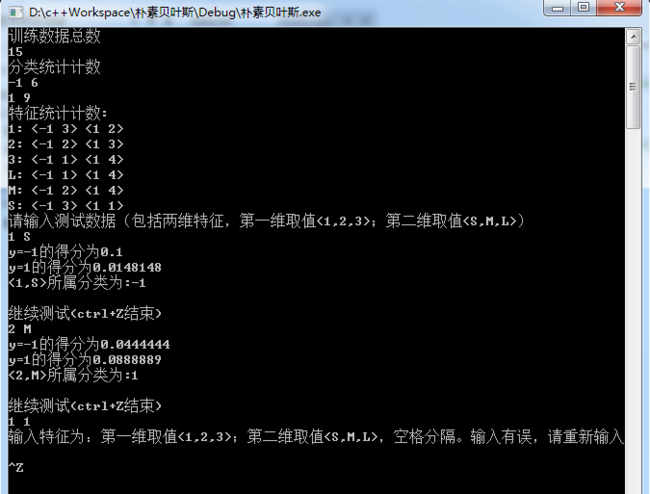
程序运行结果:
本例中,参数估计采用的是贝叶斯估计,有时间再把拉普拉斯平滑加上。