多核编程中的任务随机竞争模式的概率分析
多核编程中的任务随机竞争模式的概率分析
前一篇
多核编程中的任务分组竞争模式中谈到了让任务分组竞争以解决多核CPU遇到的锁竞争导致的饥饿问题。
但是并不是任意的共享数据都能够设计成进行分组竞争的模式,比如最常用的需要用于查找的数据结构,当数据结构分成多个子数据结构后,每次查找时,不能指定查找某个特定的子数据结构,而必须进行二级查找,先在整个数据结构内找到对应的子数据结构(不加锁),然后再在子数据结构中查找(加锁)。如果同时多个任务进行查找,有可能查找的数据分布在不同的子数据结构里,也可能分布在同一子数据结构中。当查找分布在同一子数据结构时,这时就有可能发生锁竞争现象,从而引起CPU饥饿的发生。
在这种分布式数据结构的随机锁竞争中,需要知道的是在一个k个核的CPU上,需要的任务数m和划分的子数据结构个数n为多少时,才能保证至少有k个任务在同时运行的概率不低于给定的概率P。
首先m必须大于等于k,否则无法保证至少有k个任务在运行。子数据结构个数N也必须大于K,否则出现竞争的任务组数将少于k个,从而无法保证至少有k个任务在运行,当然n越大,任务出现竞争的概率就越小,同时运行的任务数量就越多,不妨设n大于等于m。在实际情况中,n并不是越大越好,当 n过大时,由于锁的数量和n相等,会导致锁占用过多的系统资源。
下面就来计算一下至少有k个任务在同时运行的概率,考虑一种最坏情况的假设:假设有两个任务在访问同一个子数据结构 ,那么它们一定会发生锁竞争。在这种最坏假设下,要保证至少有k个任务在同时运行 ,实际上相当于m个任务至少访问了k个不同的子数据结构。
假设访问每个子数据结构的任务数为Xi ( 0 <= Xi <= m, i∈
{1,2,…n}),这样可以得到以下整数方程:
X1+X2+…+Xn = m
(方程1)
要保证至少有k组任务在竞争,实际上相当于X1,X2…Xn中必须至少有k个大于0,这样至少有k个任务在运行的概率相当于上述方程满足,X2…Xn中必须至少有k个大于0的解的个数和所有可能解的个数的比值。
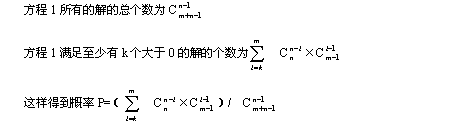
下面是对这个概率公式的一些实际计算结果:
当k=2
(2
核CPU
), m=2
(2
个任务), P=(n-1) / (n+1) 当n=4时,P=0.6; 当n=8时,P=7/9 =0.7778; 当n=16时, P=15/17=0.882
当k=2
(2
核CPU
), m=4
(4
个任务), P=(n-1) (n
+3)/ ((n+1)(n+2)) + 9 (n-1)/((n+3)(n+2)(n+1))
当n=4时,P=0.83; 当n=8时,P=0.919; 当n=16时, P=0.954
当k=4
(4
核CPU
), m=4
(4
个任务), P=(n-1) (n-2)(n-3)/ ((n+1)(n+2)(n+3))
当n=4时,P=0.0286; 当n=8时,P=0.212; 当n=16时, P=0.47; 当n=32时,P=0.687
当k=4
(4
核CPU
), m=6
(6
个任务), P = [ 1+12(n+15)/((n+4)(n+5)) ]
×[(n-1)(n-2)(n-3)]/ [(n+1)(n+2)(n+3)]
当n=8时,P=0.587; 当n=16时, P=0.886; 当n=32时,P=0.978
从上面计算可以看出,当CPU核数固定时,任务数m越多,则概率愈大 ,子数据结构个数n越大,概率愈大。一般来说任务数最好比核数大一倍,这样得出的概率会大一些。
以上计算的是在最坏情况下的概率,实际情况中,由于两个任务在竞争同一个子数据结构时并不一定会发生竞争现象,因为可能发生任务A在进行锁操作时,任务B正在执行不需要加锁部分的代码,因此实际的概率会大于上面计算出的最坏情况下的概率。
分布式数据结构随机锁竞争和无锁编程的性能比较
在使用了随机锁竞争的分布式数据结构中,并行化的加速比期望值等于前面所计算出的概率×CPU核数,因此只要将概率保持大于一定的值,那么加速比是可以得到保证的,并且只要加大任务个数和子数据结构个数,那么加速比的期望值就会增加。另外分布式数据结构中相比于单任务的数据结构其操作要复杂一些,增加了一些计算开销,另外加上锁的计算开销,因此加速比要打一个较大的折扣。但是分布式数据结构的好处在于它的加速比系数不会随CPU核数的增加而降低,程序的性能是随着核数的增加而线形增加的(前提是在数据 结构中的元素个数足够多的情况下)。
在无锁编程中,由于使用了原子操作,原子操作是串行化的,虽然原子操作占的比重很小,但是这种串行化反映到加速比计算上需要按照阿姆尔达定律来计算,因此其性能同样不容乐观,会随着CPU核数的增加而降低。以一个无锁的FIFO队列为例,在进队操作时需要使用一条CAS原子操作,由于队列操作本身就很简单,因此昂贵的CAS操作所占的比例也不容小觑,在这种队列操作中,CAS所占的比例估计要达到20%左右(具体的数据需要通过测试才能确定),按照阿姆尔达定律,在一个8核的 CPU上的加速比系数将为3.33, 在一个64核CPU上,其加速比将小于5,当然这是只考虑队列操作没有考虑程序中其他并行操作的极端情况,但是不管怎么说,采用无锁编程的话,加速比系数会随CPU核数的增加而降低。
另外无锁编程相比于单任务编程,其代码也变复杂了,也增加了额外的计算开销,加速比也需要另外打一个折扣。
如果将分布式数据结构和单核时的多任务编程相比,则分布式数据结构中,仅仅增加了定位到子数据结构的开销,如果是查找类型的数据结构,子表的查找时间缩小了,实际上增加的开销小于定位子数据结构的开销。因此分布式数据结构增加的开销所占的比例是非常小的,其性能近似(略低)于单核时的多任务编程。
在CPU核数较少时,无锁编程的性能可能会优于分布式数据结构,并且优于单核多任务编程的性能,但是当CPU核数增加到一定程度时,分布式数据结构的性能优势就体现出来了。采用分布式数据结构可以复用部分单任务时的数据结构代码,采用加锁机制容易被程序员理解,并且实现的功能不受限制。而无锁编程则难度非常高,远非普通程序员所能掌握,并且实现的功能受到限制,比如实现一个无锁的队列,如果想要给队列加一个计数来掌握队列中有多少元素,采用无锁编程实现估计就很难行得通了,而这在有锁编程中只是一个简单得不能再简单的东西。因此对程序员来说,分布式数据结构是多核时代必需掌握的技术,而无锁编程也许可以用在某些无法使用分布式数据结构的特定场合。
需要说明的是前面对概率的计算隐含了一个前提,就是每个任务在访问各个子数据结构时的概率是相同的,这要求各个子数据结构必须是负载均衡的,否则如果访问各个子数据结构的概率不相同的话,计算出的结果会小于前面的计算结果,考虑一种最极端的情况,所有的数据都在一个子数据结构里,那么所有的任务都将竞争同一个子数据结构,那么问题倒退回多核编程中的锁竞争难题一文中描述一样的情况,这是一种可能比阿姆尔达定律更糟糕的情况。100%的负载均衡是做不到的,所幸可以通过一定的手段来使数据尽量变得均衡,使得数据能够相对较均匀地分布在各个子数据结构中,这样就不会对最终的概率产生较大影响。
参考资料:
[1]《并行编程模式》Timothy Mattson等著 敖富江译
[2]《多核程序设计技术》Shameem Akhter等著 李宝峰等译
[3] “An Optimistic Approach to Lock-Free FIFO Queues”
Edya Ladan-Mozes and Nir Shavit
[4]《并行程序设计》 Barry Wilkinson, Michael Allen著,陆鑫达等译
[5]“Fast and lock-free concurrent priority queues for multi-thread systems” H. Sundell, Philippas Tsigas, Journal of Parallel and Distributed Computing. 2005
[6]
“
NOBLE: A Non-Blocking Inter-Process Communication Library.
”
H. S
UNDELL
, P. T
SIGAS
. Proceedings ofthe 6th Workshop on Languages, Compilers and Runtime Systems for Scalable omputers (LCR’02), Lecture Notes in Computer Science, Springer Verlag, 2002.
Trackback: http://tb.blog.csdn.net/TrackBack.aspx?PostId=1689789